LA FORMA Y EL NÚMERO EN SITUACIONES DE LA COTIDIANIDAD. : Elementos y propiedades básicas de una ecuación de 1er grado.

Las ecuaciones de primer grado son conocidos también como ecuaciones lineales y tiene la siguiente forma general:

Esta ecuación lineal de una incógnita tiene una única solución; es decir, la ecuación es COMPATIBLE DETERMINADA.

La solución de esta ecuación, después de despejar «x» será:

Donde el valor: «-b/a» será el conjunto solución (C.S.) de la ecuación de primer grado.

Elementos de una Ecuación Lineal

Debemos entender que elementos intervienen en una ecuación lineal, para ello nos basaremos en el siguiente gráfico:

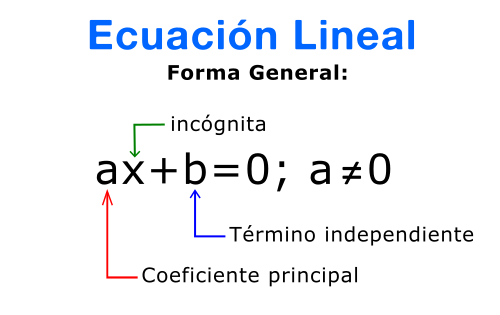
Donde:

x: es la variable o incógnita.
a: coeficiente principal.
b: término independiente.

Elementos de una ecuación

En las ecuaciones distinguimos varios elementos :

Incógnita: La letra (o variable) que figura en la ecuación.
Miembro: Es cada una de las dos expresiones algebraicas separadas por el signo "=".
Término: Cada uno de los sumandos que componen los miembros de la ecuación.
Grado: Es el mayor de los exponentes de las incógnitas, una vez realizadas todas las operaciones (reducir términos semejantes).

Propiedades de las igualdades

Para la resolución de ecuaciones algebraicas es preciso tener en cuenta las propiedades elementales de las igualdades:

Cuando se suma o resta un mismo número a los dos miembros de una ecuación se obtiene una ecuación equivalente.
Si los dos miembros de una ecuación se multiplican o dividen globalmente por un mismo número, el resultado es también una ecuación equivalente. Cuando se divida tiene que ser por un número distinto de cero.

Estas propiedades suelen utilizarse para transponer términos, mediante dos técnicas complementarias:

Sumar en ambos miembros de una ecuación el valor opuesto (cambiado de signo) de un término que se quiera transponer de un miembro a otro.
Multiplicar ambos miembros por el inverso del término que se quiera transponer.

Propiedades de las desigualdades

Para resolver inecuaciones se aplican las siguientes propiedades de las desigualdades:

Cuando se suma o resta un mismo término en ambos miembros de una inecuación se obtiene una inecuación equivalente.
Si se multiplican o dividen los dos miembros de una inecuación por un número o cantidad positivos, la inecuación resultante es equivalente; si este número o cantidad son negativos, la inecuación resultante es también equivalente, pero ha de invertirse el signo de la desigualdad.

Estas propiedades se utilizan, al igual que en las ecuaciones, para transponer términos y obtener las raíces o soluciones.