LA FORMA Y EL NÚMERO EN SITUACIONES DE LA COTIDIANIDAD.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 1° - Matemáticas |
| Libro: | LA FORMA Y EL NÚMERO EN SITUACIONES DE LA COTIDIANIDAD. |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 06:31 |
Tabla de Contenidos
- 1. Razones y proporciones y la distribución equitativa de los bienes y servicios en la comunidad.
- 2. Magnitudes: directamente proporcionales, inversamente proporcionales.
- 3. Regla de tres simple en el manejo de los recursos naturales y económicos de la comunidad.
- 4. Regla de tres compuesta en actividades económicas de nuestro entorno.
- 5. Expresiones algebraicas y valor numérico de una variable en una ecuación de 1er grado.
- 5.1. Ecuaciones de 1er grado en actividades del entorno.
- 5.2. Elementos y propiedades básicas de una ecuación de 1er grado.
- 5.3. Procedimiento para la determinación del valor numérico de una variable en una ecuación de 1er grado.
- 5.4. Valor numérico de expresiones algebraicas | Ejemplo 1
- 5.5. Valor numérico de expresiones algebraicas | Ejemplo 2
- 5.6. Valor numérico de expresiones algebraicas | Ejemplo 3
- 5.7. *Planteamiento y Resolución por medio de ecuaciones de 1er grado de problemas de nuestro entorno.
1. Razones y proporciones y la distribución equitativa de los bienes y servicios en la comunidad.
1- Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:
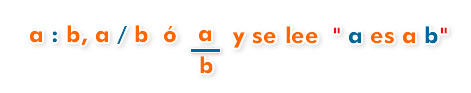
Ejemplo:
En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?
La relación entre el número de mujeres y el número de hombres es de "10 es a 18" , otra forma de leerlo es "10 de 18 "
El término a es el antecedente de la razón y el b, el consecuente.

El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón

Dos o más razones son equivalentes cuando tienen igual valor.
1.1- Resolución de problemas:
Veamos cómo resolver problemas de razones:
Ejemplo 1:
La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.
Solución:
Si las edades son a y b
Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:
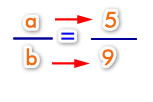
Ahora volvemos a los datos del problema:
Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:
![]()
Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :


Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :
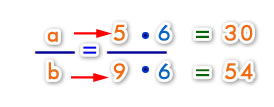
2- Proporciones
Una proporción es la igualdad de dos razones.
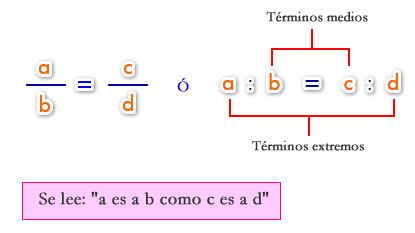
2.1- Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:


1.1. Razones | qué es una razón | Ejemplos
1.2. Qué es una proporción Ejemplos
2. Magnitudes: directamente proporcionales, inversamente proporcionales.
Proporcionalidad: directa e inversaPara comprender el concepto de proporcionalidad, directa o inversa, debemos comenzar por comprender el concepto de razón.
Razón y proporción numérica
Razón entre dos números
Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos.
Entonces:
Razón entre dos números a y b es el cociente entre |
|
Por ejemplo, la razón entre 10 y 2 es 5 , ya que |
Y la razón entre los números 0,15 y 0,3 es |
Proporción numérica
Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver como se comportan entre ellas, estaremos hablando de una proporción numérica.
Entonces:
| Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que entre c y d . | |
Es decir | |
| Se lee “ a es a b como c es a d” | |
Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.
Es decir |
| En la proporción | hay cuatro términos; a y d se llaman extremos , c y b se llaman medios. |
La propiedad fundamental de las proporciones es: en toda proporción, el producto de los extremos es igual al de los medios. |
Así, en la proporción anterior |
se cumple que el producto de los extremos nos da 2 x 20 = 40 y el producto de los medios nos da 5 x 8 = 40
![]()
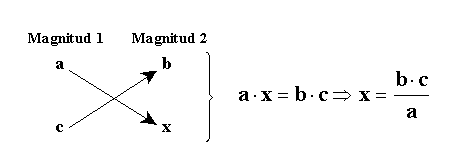
Comprendido el concepto de proporción como una relación entre números o magnitudes, ahora veremos que esa relación puede darse en dos sentidos:
Las dos magnitudes pueden subir o bajar (aumentar o disminuir) o bien si una de las magnitudes sube la otra bajo y viceversa.
Si ocurre, como en el primer caso, que las dos magnitudes que se comparan o relacionan pueden subir o bajar en igual cantidad, hablaremos de Magnitudes directamente proporcionales .
Si ocurre como en el segundo caso, en que si una magnitud sube la otra baja en la misma cantidad, hablaremos de Magnitudes inversamente proporcionales .
2.1. Diferencias entre magnitudes directamente proporcionales o inversamente proporcionales
3. Regla de tres simple en el manejo de los recursos naturales y económicos de la comunidad.
La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.
Para hacer una regla de 3 simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad.
Regla de 3 simple directa
Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa.
Colocaremos en una tabla los 3 datos (a los que llamamos “a”, “b” y “c”) y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:
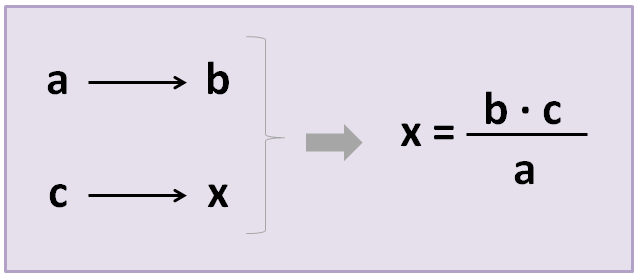
Para ver un ejemplo, vamos a resolver el mismo problema de proporcionalidad directa que vimos la semana pasada, ahora aplicando la regla de 3 simple:
Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?
Vamos a hacer la tabla con los 3 datos y la incógnita (“x”), y hallaremos “x” con la fórmula que acabamos de aprender:
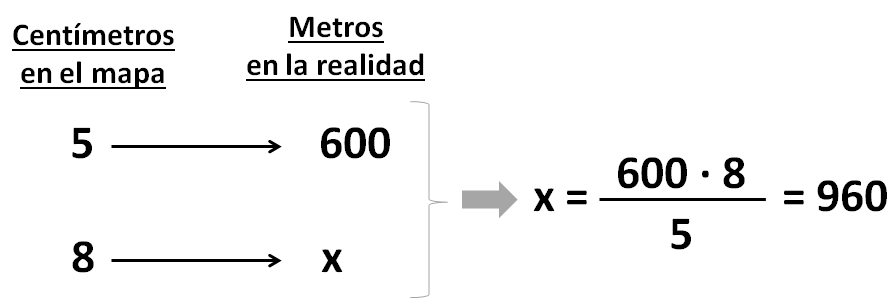
Solución: El parque se encuentra a 960 metros del hotel
Regla de 3 simple inversa
Ahora vamos a ver cómo aplicar la regla de 3 simple en casos de proporcionalidad inversa. Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:
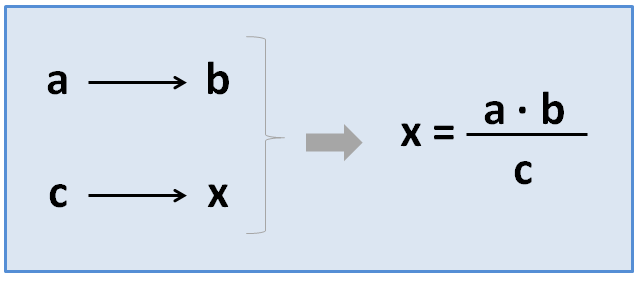
Vamos a ver un ejemplo con el mismo problema que resolvimos en el post de la semana anterior:
Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?
Colocamos los datos en una tabla y aplicamos la fórmula de la regla de 3 simple inversa:
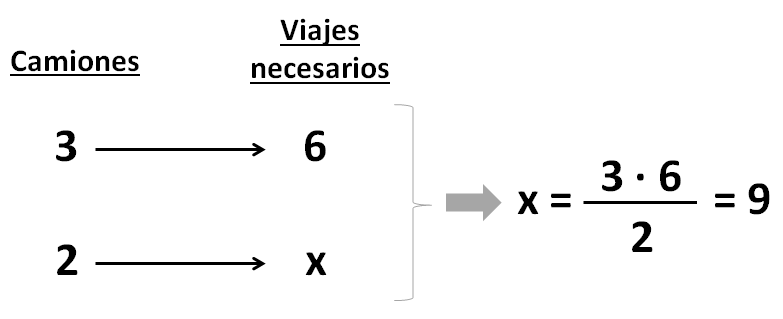
Solución: Ayer los 2 camiones hicieron 9 viajes.
3.1. Regla de tres simple directa | Ejemplo 1
3.2. Regla de tres simple directa | Ejemplo 2
3.3. Regla de tres Simple Inversa | Ejemplo 1
3.4. Regla de tres Simple Inversa | Ejemplo 2
4. Regla de tres compuesta en actividades económicas de nuestro entorno.
Como ya sabrás, la regla de 3 simple relaciona dos magnitudes proporcionales. La proporcionalidad puede ser directa o inversa.
- Proporcionalidad directa
- Proporcionalidad inversa
La diferencia de la regla de 3 simple con la regla de 3 compuesta es que en la primera se relacionan dos magnitudes y en la segunda se relacionan tres o más magnitudes. Aunque en este post solo resolveremos problemas con 3 magnitudes, la forma de resolver los problemas con más magnitudes es la misma.
Ejemplo de regla de 3 compuesta con las dos proporcionalidades directas.
Hemos ido a la fuente del pueblo para recoger agua. Sabemos que 5 botellas de agua, de 2 litros cada una, pesan 10 kilos. ¿Cuánto pesan 2 botellas de 3 litros cada una?
Las tres magnitudes que tenemos en el problema son: botellas, litros y kilos. Escribimos la relación entre ellas sabiendo que:
5 botellas, 2 litros, 10 kilos
2 botellas, 3 litros, X kilos
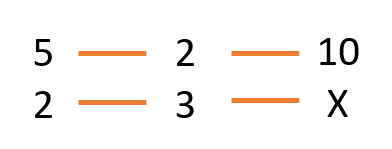
Ahora tenemos que averiguar la relación entre las magnitudes, comparando siempre con la magnitud donde esté la incógnita X.
Comparamos botellas con kilos: Si hay menos botellas entonces pesarán menos. Tienen proporcionalidad directa.
Comparamos litros con kilos: Si hay más litros entonces pesarán más. Tienen proporcionalidad directa.
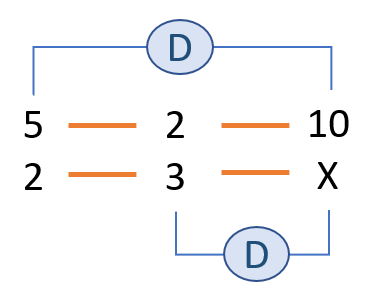
Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. La primera fracción es donde está la incógnita (esto no es obligatorio, pero ayuda para después resolverlo). Después, igualamos a la multiplicación de las dos fracciones:
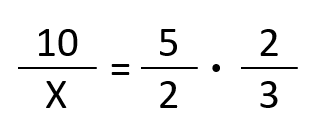
Y resolvemos:
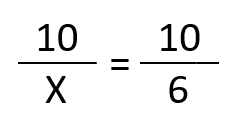
Podemos despejar la X haciendo los productos cruzados:
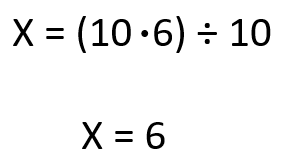
2 botellas, de 3 litros cada una, pesan 6 kilos.
En 4 días, 6 impresoras han impreso 100 libros. ¿Cuántos días tardarán en imprimir 50 libros si tenemos 4 impresoras?
Las magnitudes que tenemos en el problema son: días, impresoras y libros. La relación entre ellas es:
4 días, 6 impresoras, 100 libros.
X días, 4 impresoras, 50 libros
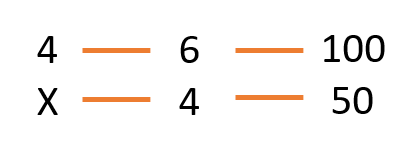
Vemos la proporcionalidad entre las magnitudes:
Si hay que hacer menos libros entonces se necesitan menos días. Proporcionalidad directa.
Si hay menos impresoras entonces se necesitan más días. Proporcionalidad inversa.
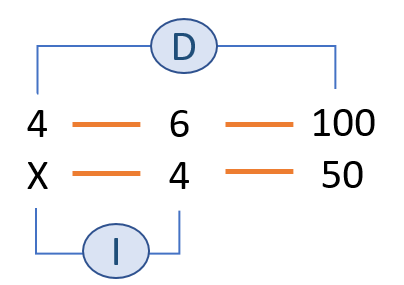
Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. ¡OJO! La magnitud que es inversa debemos invertirla, es decir, el denominador pasa a ser numerador y el numerador pasa a ser denominador.
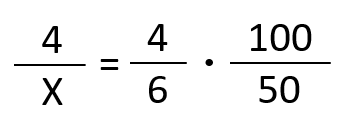
Ahora resolvemos como el problema anterior, por el método de los productos cruzados.
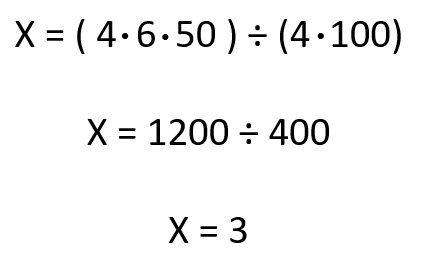
Para imprimir 50 libros, 4 impresoras tardan 3 días.
Espero que te haya gustado el post de hoy y hayas aprendido a resolver problemas con la regla de 3 compuesta.
4.1. Regla de tres compuesta | Ejemplo 1
4.2. Regla de tres compuesta | Ejemplo 2
4.3. Regla de tres compuesta Ejemplo 3
5. Expresiones algebraicas y valor numérico de una variable en una ecuación de 1er grado.
Qué es una expresión algebraica
Una expresión algebraica es una combinación de números, letras y operaciones.
3vp5+4x es una expresión algebraica.
Valor numérico de una expresión algebraica
El valor numérico de una expresión algebraica es el resultado que se obtiene de sustituir las variables por números y realizar las operaciones resultantes.
Siguiendo con el ejemplo del apartado anterior, el valor numérico cuando v = 2, p= -1 y x = 0 es:
3vp5+4x = 3·2·(-1)5+4·0 = 6·(-1)+0 = -6
Expresiones algebraicas importantesLos monomios son expresiones algebraicas en las que las únicas operaciones que afectan a las letras son la multiplicación y la potenciación de exponente positivo.
Ejemplo:
5x2yz ó 8ab2c3 son ejemplos de monomios.
Un binomio es la suma o resta de dos monomios; un trinomio es la suma o resta de tres monomios,…y sucesivamente hasta llegar a un polinomio que es la suma o resta de muchos monomios.
-3x2+y3 es un bonimio,
8a6-4b5+2c3 es un trinomio y,
3x5-4x3-2x+7 es un polimonomio.
5.1. Ecuaciones de 1er grado en actividades del entorno.
En cuanto a las matemáticas, las ecuaciones de primer grado son la introducción al álgebra. Su comprensión es imprescindible para cualquier tipo de ecuaciones: ecuaciones de segundo grado o de grado mayor, exponenciales, irracionales, etc. y para los sistemas de ecuaciones.
En cuanto a la vida real, aunque en un principio no se piense así, las ecuaciones son una herramienta de gran utilidad que nos permiten resolver numerosos problemas a los que nos enfrentamos diariamente. Podemos comprobarlo en la sección de problemas.
Como ya indica su nombre, en las ecuaciones de primer grado, la parte literal de los monomios no tiene exponente (por ejemplo, 3x puede formar parte de una ecuación pero 3x2 no porque sería de segundo grado). Justamente este hecho nos asegura que, en caso de existir solución, hay sólo una (excepto el caso especial en qué hay infinitas soluciones).
Decimos "en caso de existir solución" ya que en ocasiones las ecuaciones no tienen solución. Por ejemplo, la ecuación x = x + 1 (cuya lectura es "un número que es igual a su consecutivo") no tiene solución porque esto nunca se cumple. De hecho, la ecuación se reduce a 1 = 0, lo cual es imposible.
Si obtenemos una igualdad imposible, la ecuación no tiene solución.
Ejemplo:
Si obtenemos la ecuación 1 = 0 , la ecuación inicial no tiene solución.
Si obtenemos una igualdad que siempre se cumple, cualquier valor es solución de la ecuación, es decir, la solución es todos los reales.
Ejemplo:
Si obtenemos la igualdad 0 = 0 , la solución es todos los reales:
Pasamos las x's a un lado de la igualdad (izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
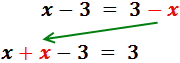
Sumamos los monomios con x’s:
![]()
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
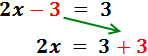
Sumamos los monomios de la derecha:
![]()
El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
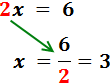
Por tanto, la solución de la ecuación es x = 3.
5.2. Elementos y propiedades básicas de una ecuación de 1er grado.
Las ecuaciones de primer grado son conocidos también como ecuaciones lineales y tiene la siguiente forma general:
ax + b = 0; a ≠ 0
Esta ecuación lineal de una incógnita tiene una única solución; es decir, la ecuación es COMPATIBLE DETERMINADA.
La solución de esta ecuación, después de despejar «x» será:
x = -b/a
Donde el valor: «-b/a» será el conjunto solución (C.S.) de la ecuación de primer grado.
Elementos de una Ecuación Lineal
Debemos entender que elementos intervienen en una ecuación lineal, para ello nos basaremos en el siguiente gráfico:
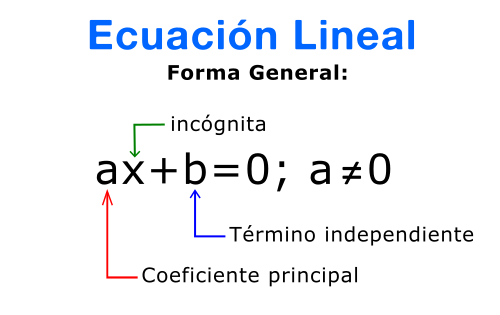
Donde:
x: es la variable o incógnita.
a: coeficiente principal.
b: término independiente.
Elementos de una ecuación
En las ecuaciones distinguimos varios elementos :
Incógnita: La letra (o variable) que figura en la ecuación.
Miembro: Es cada una de las dos expresiones algebraicas separadas por el signo "=".
Término: Cada uno de los sumandos que componen los miembros de la ecuación.
Grado: Es el mayor de los exponentes de las incógnitas, una vez realizadas todas las operaciones (reducir términos semejantes).
Propiedades de las igualdades
Para la resolución de ecuaciones algebraicas es preciso tener en cuenta las propiedades elementales de las igualdades:
- Cuando se suma o resta un mismo número a los dos miembros de una ecuación se obtiene una ecuación equivalente.
- Si los dos miembros de una ecuación se multiplican o dividen globalmente por un mismo número, el resultado es también una ecuación equivalente. Cuando se divida tiene que ser por un número distinto de cero.
Estas propiedades suelen utilizarse para transponer términos, mediante dos técnicas complementarias:
- Sumar en ambos miembros de una ecuación el valor opuesto (cambiado de signo) de un término que se quiera transponer de un miembro a otro.
- Multiplicar ambos miembros por el inverso del término que se quiera transponer.
Propiedades de las desigualdades
Para resolver inecuaciones se aplican las siguientes propiedades de las desigualdades:
- Cuando se suma o resta un mismo término en ambos miembros de una inecuación se obtiene una inecuación equivalente.
- Si se multiplican o dividen los dos miembros de una inecuación por un número o cantidad positivos, la inecuación resultante es equivalente; si este número o cantidad son negativos, la inecuación resultante es también equivalente, pero ha de invertirse el signo de la desigualdad.
Estas propiedades se utilizan, al igual que en las ecuaciones, para transponer términos y obtener las raíces o soluciones.
5.3. Procedimiento para la determinación del valor numérico de una variable en una ecuación de 1er grado.
El valor numérico de una expresión algebraica es el número que resulta de sustituir las variables de la de dicha expresión por valores concretos y completar las operaciones. Una misma expresión algebraica puede tener muchos valores numéricos diferentes, en función del número que se asigne a cada una de las variables de la misma.
La única precaución necesaria es respetar el orden y las propiedades de las operaciones. Por ejemplo, no tiene sentido calcular el valor numérico de ![]() para
para ![]() , porque no se puede dividir entre cero. En la siguiente animación puedes ver cómo se haría la sustitución para calcular el valor numérico de
, porque no se puede dividir entre cero. En la siguiente animación puedes ver cómo se haría la sustitución para calcular el valor numérico de ![]() para
para ![]() ,
, ![]() y
y ![]() . Faltaría completar las operaciones (el resultado final es
. Faltaría completar las operaciones (el resultado final es ![]() ), pero lo más importante es que te fijes en los elementos que se añaden al hacer la sustitución: El punto del producto entre el 3 y el 2 (valor de
), pero lo más importante es que te fijes en los elementos que se añaden al hacer la sustitución: El punto del producto entre el 3 y el 2 (valor de ![]() ) y los paréntesis de -1 (valor de
) y los paréntesis de -1 (valor de ![]() ), que son necesarios para indicar la multiplicación con el 2.
), que son necesarios para indicar la multiplicación con el 2.
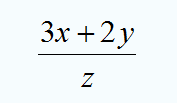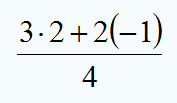
El punto de la multiplicación se puede omitir entre el 2 y el -1 gracias a los paréntesis, aunque escribirlo no sería un error. Fíjate en los siguientes ejemplos, en los que puedes ver cómo calcular el valor numérico de varias expresiones, paso a paso, para distintos valores de las variables.
| EXPRESIÓN ALGEBRAICA | VALORES DE LAS VARIABLES | VALOR NUMÉRICO PARA ESOS VALORES DE LAS VARIABLES |
5.4. Valor numérico de expresiones algebraicas | Ejemplo 1
5.5. Valor numérico de expresiones algebraicas | Ejemplo 2
5.6. Valor numérico de expresiones algebraicas | Ejemplo 3
5.7. *Planteamiento y Resolución por medio de ecuaciones de 1er grado de problemas de nuestro entorno.
*