LA FORMA Y EL NÚMERO EN SITUACIONES DE LA COTIDIANIDAD.
4. Regla de tres compuesta en actividades económicas de nuestro entorno.
Como ya sabrás, la regla de 3 simple relaciona dos magnitudes proporcionales. La proporcionalidad puede ser directa o inversa.
- Proporcionalidad directa
- Proporcionalidad inversa
La diferencia de la regla de 3 simple con la regla de 3 compuesta es que en la primera se relacionan dos magnitudes y en la segunda se relacionan tres o más magnitudes. Aunque en este post solo resolveremos problemas con 3 magnitudes, la forma de resolver los problemas con más magnitudes es la misma.
Ejemplo de regla de 3 compuesta con las dos proporcionalidades directas.
Hemos ido a la fuente del pueblo para recoger agua. Sabemos que 5 botellas de agua, de 2 litros cada una, pesan 10 kilos. ¿Cuánto pesan 2 botellas de 3 litros cada una?
Las tres magnitudes que tenemos en el problema son: botellas, litros y kilos. Escribimos la relación entre ellas sabiendo que:
5 botellas, 2 litros, 10 kilos
2 botellas, 3 litros, X kilos
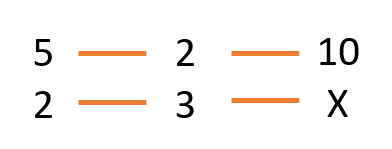
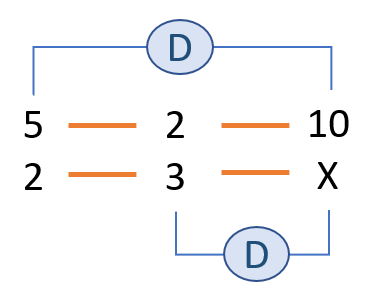
Ahora tenemos que averiguar la relación entre las magnitudes, comparando siempre con la magnitud donde esté la incógnita X.
Comparamos botellas con kilos: Si hay menos botellas entonces pesarán menos. Tienen proporcionalidad directa.
Comparamos litros con kilos: Si hay más litros entonces pesarán más. Tienen proporcionalidad directa.
Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. La primera fracción es donde está la incógnita (esto no es obligatorio, pero ayuda para después resolverlo). Después, igualamos a la multiplicación de las dos fracciones:
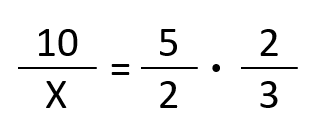
Y resolvemos:
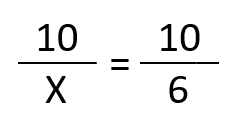
Podemos despejar la X haciendo los productos cruzados:
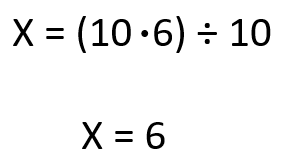
2 botellas, de 3 litros cada una, pesan 6 kilos.
En 4 días, 6 impresoras han impreso 100 libros. ¿Cuántos días tardarán en imprimir 50 libros si tenemos 4 impresoras?
Las magnitudes que tenemos en el problema son: días, impresoras y libros. La relación entre ellas es:
4 días, 6 impresoras, 100 libros.
X días, 4 impresoras, 50 libros
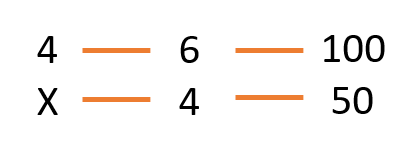
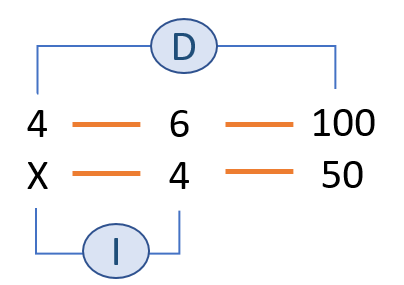
Vemos la proporcionalidad entre las magnitudes:
Si hay que hacer menos libros entonces se necesitan menos días. Proporcionalidad directa.
Si hay menos impresoras entonces se necesitan más días. Proporcionalidad inversa.
Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. ¡OJO! La magnitud que es inversa debemos invertirla, es decir, el denominador pasa a ser numerador y el numerador pasa a ser denominador.
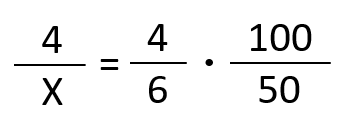
Ahora resolvemos como el problema anterior, por el método de los productos cruzados.
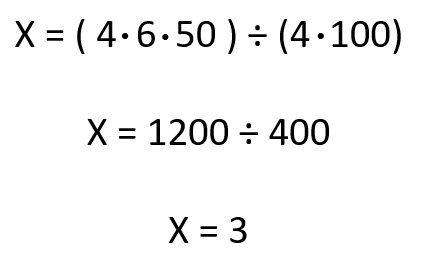
Para imprimir 50 libros, 4 impresoras tardan 3 días.
Espero que te haya gustado el post de hoy y hayas aprendido a resolver problemas con la regla de 3 compuesta.