LA FORMA, EL NÚMERO Y LA RELACIÓN CON EL ENTORNO NATURAL Y CULTURAL

En el campo de las matemáticas, dos figuras geométricas pueden ser congruentes cuando éstas figuras tienen las mismas dimensiones y la misma forma sin importar cuál sea su posición u orientación, en otras palabras, si existe una isometría que los relaciona: una transformación que puede ser de traslación, rotación y/o reflexión. Las partes relacionadas entre las figuras congruentes se conocen con el nombre de figuras homólogas o correspondientes.

El término congruencia tiene varios significados dependiendo del punto de vista matemático. Por esta razón, dentro del campo de la geometría euclidiana, la congruencia es equivalente a una igualdad matemática la igual que en aritmética y álgebra. En el área de la geometría analítica, la congruencia se define como dos figuras determinadas por puntos que se encuentran sobre un sistema de coordenadas cartesianas las cuales son congruentes entre sí.

En el campo de las matemáticas, dos figuras de puntos pueden ser congruentes cuando tienen los lados iguales y del mismo tamaño si existe una isometría que los relaciona. En otras palabras, dos figuras pueden llegar a ser congruentes si tienen la misma forma y tamaño, sin importar que su posición u orientación sean diferentes. Las partes que coinciden en las figuras congruentes se llaman homólogas o correspondientes.

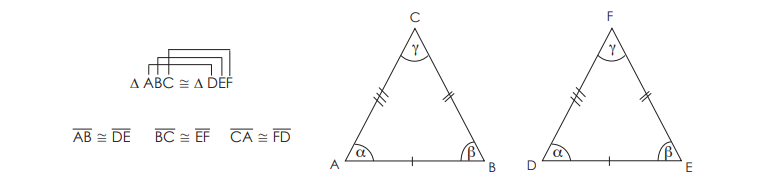
Dos o más figuras son congruentes si se cumple que son exactamente iguales tanto en forma como en tamaño, es decir si sus lados y sus ángulos respectivos tienen igual medida, aunque su posición y orientación sean distintas. El símbolo de congruencia es ( ≅ ). Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.