LA FORMA, EL NÚMERO Y LA RELACIÓN CON EL ENTORNO NATURAL Y CULTURAL
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 1° - Matemáticas |
| Libro: | LA FORMA, EL NÚMERO Y LA RELACIÓN CON EL ENTORNO NATURAL Y CULTURAL |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 06:54 |
Descripción
a
Tabla de Contenidos
- 1. Conceptos de relación de semejanza de figuras geométricas en la naturaleza y la diversidad cultural.
- 2. Congruencia de triángulos en el entorno.
- 3. Triángulos semejantes en la tecnología.
- 4. Puntos y Rectas notables de triángulos.
- 5. Teorema de Pitágoras en las culturas ancestrales.
- 6. Elementos de la Circunferencia y el Círculo: Radio, Diámetro, Cuerda, Arco circunferencial, Sector circular y Segmento circular.
- 7. El valor de “π” y los saberes matemáticos ancestrales e interculturales.
1. Conceptos de relación de semejanza de figuras geométricas en la naturaleza y la diversidad cultural.
La geometría (del latín geometrĭa, que proviene del idioma griego γεωμετρία, geo tierra y metria medida: Medida de la tierra), es una parte de la matemática que se encarga de estudiar las propiedades y las medidas de las figuras geométricas en el plano o el espacio.
Se desarrolló extraordinariamente en Egipto de forma paralela a la agrimensura. Con la aplicación de sus conclusiones se pretendía resolver los frecuentes problemas de delimitación de los terrenos cultivables que ocasionaban las continuas crecidas y bajadas del nivel del Nilo. Posteriormente,durante el siglo III a. C. en Grecia, Euclides en su obra «Los Elementos» configuró la geometría en forma axiomática, es decir la organizó de forma científica y rigurosa mediante axiomas (las proposiciones que se encargan de relacionar los conceptos) para poder dar lugar a teorías.Esta organización de la geometría y sus problemas constituye la llamada geometría clásica o geometria euclidea.

Una simple mirada al entorno que nos rodea nos permite observar que las figuras y las relaciones geométricas abstractas que encontramos en los libros de matemáticas se encuentran por todas partes y que la geometría está presente de manera directa y muy concreta en la naturaleza y en nuestra vida cotidiana.
Sin embargo las cosas de la naturaleza no obedecen estrictamente a los patrones geometricos que la geometría clasica describe.Las nubes no son esferas, las montañas no son conos, las costas no son círculos, y la corteza no es uniforme, ni un rayo de luz viaja en línea recta. La geometría de formas de la naturaleza es de tal complejidad que la geometría clásica no puede describirlas de forma completa.
Para resolver este problema el matemático francés Benoit Mandelbrot creó durante los años sesenta la Geometría Fractal. Mandelbrot molestó a los matemáticos de su época, cuando afirmó que nada en la naturaleza puede ser descrito por la geometría tradicional de los matemáticos y científicos universitarios.
Mandelbrot no solo dió cuenta de que todos los patrones en la naturaleza son similares. En realidad fue un paso más adelante: descubrió que todos estos patrones, sin importar si son los patrones de las selvas, costas, relámpagos o cualquier otro proceso natural, puede ser descrito por un tipo similar de ecuación. ¿Has notado cómo todos árboles d euna misma clase tienen un aspecto similar, pero no hay dos que sean iguales? ¿O cómo las conchas de mar y las playas son variaciones sobre el mismo tema? Eso es de lo que se tratan los fractales de Mandelbrot.
El número de los fractales en la naturaleza es verdaderamente sorprendente.Los fractales están por todas partes. Todas las plantas crecen y se desarrollan de una forma de tipo fractal. El cuerpo humano está lleno de fractales, de los bronquios, los vasos sanguíneos a la forma en que se organizan las células.De hecho, la mayoría de los efectos especiales en películas de Hollywood hoy en día usan fractales. Star Wars y El Señor de los Anillos son sólo dos de una larga lista de películas que utilizan software de fractales generados para imitar el fuego y otros efectos que aparecen en pantalla.

Documental Geometría y Naturaleza
Fractales en la Naturaleza
Ejemplos de figuras geometrícas en la naturaleza
Morning Glory y el pentágono.

La Ipomoea o Morning Glory es el nombre que reciben cientos de plantas herbáceas trepadoras cuyas flores nacen y mueren cada día. Algunas semillas de estas plantas tienen efectos laxantes y otras tienen efectos nocivos para la salud, parecidos a los del LSD(alcaloide alucinógeno). En la foto pueden ver la estrella de 5 puntas dentro de un pentágono regular cuasiperfecto
Nidos hexagonales

Las abejas utilizaban el panal -teselado en hexágonos- para almacenar la miel. Hoy traemos aquí a otras parientes suyas, pero en plan negativo. Éstas no da miel. Dan picaduras. Son las avispas. Construyen sus nidos, utilizando madera -más bien papel- y fabrican estas celdas perfectas: son prismas hexagonales perfectos, formando en ocasiones conjuntos geodésicos -casi una esfera
2. Congruencia de triángulos en el entorno.
En el campo de las matemáticas, dos figuras geométricas pueden ser congruentes cuando éstas figuras tienen las mismas dimensiones y la misma forma sin importar cuál sea su posición u orientación, en otras palabras, si existe una isometría que los relaciona: una transformación que puede ser de traslación, rotación y/o reflexión. Las partes relacionadas entre las figuras congruentes se conocen con el nombre de figuras homólogas o correspondientes.
El término congruencia tiene varios significados dependiendo del punto de vista matemático. Por esta razón, dentro del campo de la geometría euclidiana, la congruencia es equivalente a una igualdad matemática la igual que en aritmética y álgebra. En el área de la geometría analítica, la congruencia se define como dos figuras determinadas por puntos que se encuentran sobre un sistema de coordenadas cartesianas las cuales son congruentes entre sí.
En el campo de las matemáticas, dos figuras de puntos pueden ser congruentes cuando tienen los lados iguales y del mismo tamaño si existe una isometría que los relaciona. En otras palabras, dos figuras pueden llegar a ser congruentes si tienen la misma forma y tamaño, sin importar que su posición u orientación sean diferentes. Las partes que coinciden en las figuras congruentes se llaman homólogas o correspondientes.
Dos o más figuras son congruentes si se cumple que son exactamente iguales tanto en forma como en tamaño, es decir si sus lados y sus ángulos respectivos tienen igual medida, aunque su posición y orientación sean distintas. El símbolo de congruencia es ( ≅ ). Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
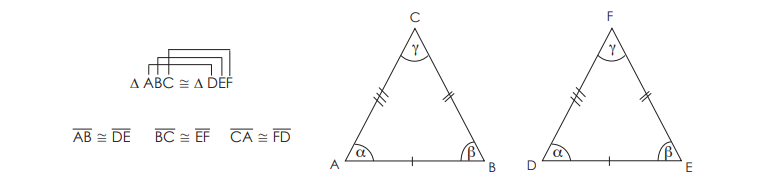
2.1. Criterios para la congruencia de triángulos: (LLL, LAL, ALA)
Criterios de congruencia
Los criterios de congruencia nos muestran la mínima información necesaria para afirmar que dos
triángulos son congruentes. Nos permiten identificar, con la información disponible, si dos triángulos son o no congruentes entre sí.
Primer criterio de congruencia: LLL
Dos triángulos son congruentes si tienen sus tres lados respectivamente iguales.
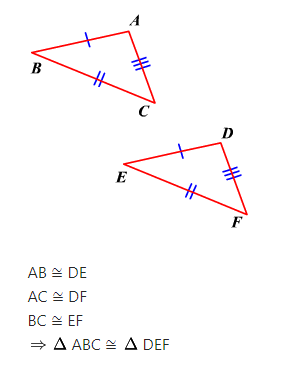
Segundo criterio de congruncia: LAL
Dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos respectivamente iguales.
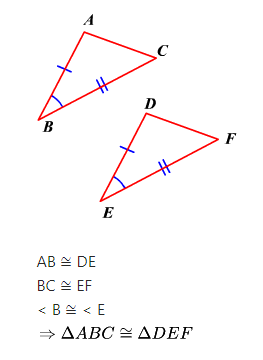
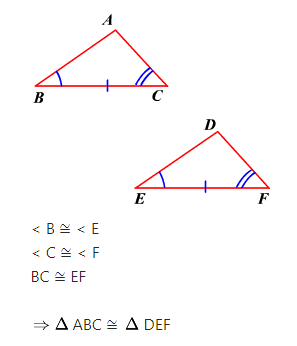
Tercer criterio de congruencia: ALA
Dos triángulos son congruentes si tienen respectivamente iguales un lado y los dos ángulos adyacentes a ese lado.
2.2. *Planteamiento y resolución de problemas relacionados a la congruencia de triángulos
*
3. Triángulos semejantes en la tecnología.
1- Semejanza
Dos polígonos son semejantes si tienen la misma forma, sus ángulos son respectivamente iguales (congruentes) y sus lados proporcionales. Es decir, uno de los polígonos es una ampliación o reducción de la otra.
Ejemplo:
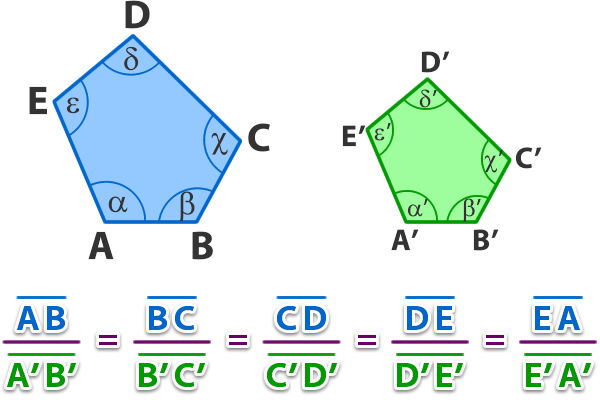
Teorema fundamental para la existencia de triángulos semejantes
Si aplicamos el teorema de fundamental de la semejanza o teorema particular de Thales en un triángulo podemos ver que toda paralela a un lado de un triángulo determina dos triángulos semejantes entre sí, ya que sus lados son proporcionales y sus ángulos son iguales.
Ejemplo:
Dado un triángulo ABC, si se traza un segmento paralelo DE a al lado BC, se obtiene otro triángulo ADE, cuyos lados son proporcionales a los del triángulo ABC.
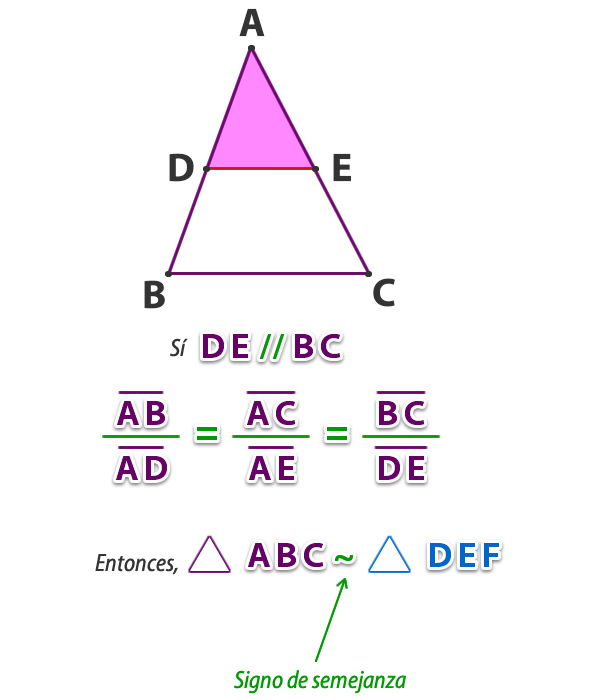
Se dirá entonces que los triángulos ABC y ADE son semejantes.
3.1. Criterios de semejanza de triángulos: (AAA, LLL, LAL)
Criterios de semejanza de triángulos
Para determinar la semejanza entre dos polígonos cualesquiera, estos se descomponen en triángulos y se verifica la semejanza entre los triángulos que los forman.
Se llaman Criterios de Semejanza de dos triángulos, a un conjunto de condiciones tales que, si se cumplen, tendremos la seguridad de que los triángulos son semejantes.
Esos criterios o casos son:

a. Criterio ángulo - ángulo (AA):
Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales (congruentes).
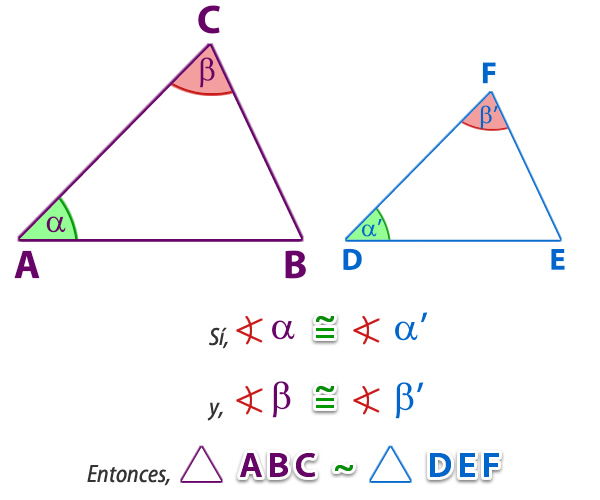
En consecuencia, el tercer ángulo también resulta igual.
b. Criterio Lado - Ángulo - Lado (LAL):
Dos triángulos son semejantes si tienen dos lados proporcionales e iguales el ángulo comprendido entre ellos.
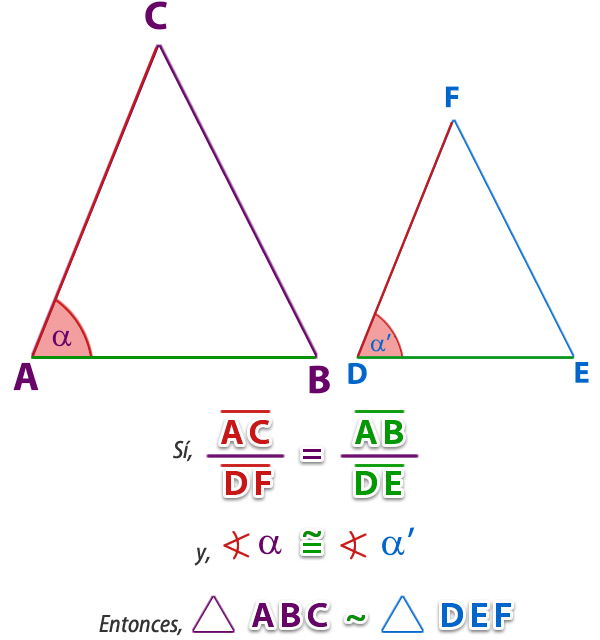
c. Criterio Lado - Lado - Lado (LLL):
Dos triángulos son semejantes si tienen sus tres lados respectivamente proporcionales.
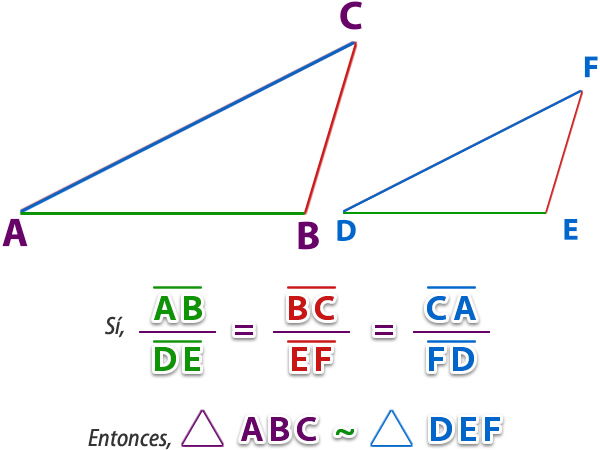
d. Criterio Lado - Lado - Ángulo (LLA):
Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo opuesto al mayor de ellos son respectivamente iguales.
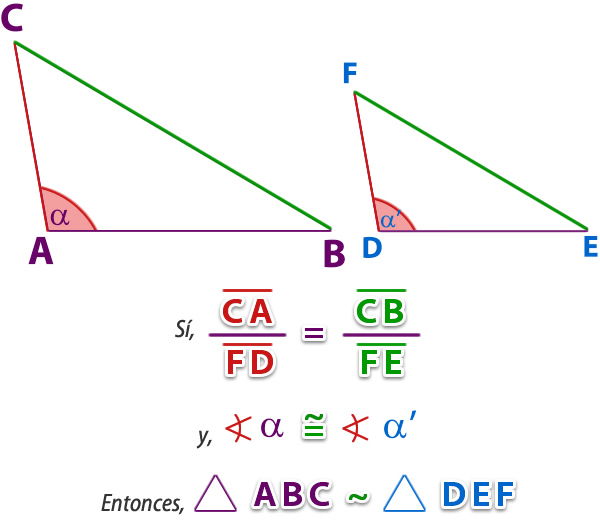
3.2. *Planteamiento y resolución de problemas relacionados a la semejanza de triángulos
*
4. Puntos y Rectas notables de triángulos.
Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo.
Además, dos lados contiguos forman uno de los ángulos interiores del triángulo que, como su propio nombre indica, tiene tres. Y, como es bien sabido, la suma de éstos es 180º.
Pues bien, sobre los triángulos hay todo un universo matemático de características, propiedades, teoremas y curiosidades. Pero no seré tan ambicioso en esta entrada (resultaría eterna) y me centraré en hablar de un grupo de rectas y puntos muy importantes, solo los más conocidos ya que hay muchos más, que se conocen como puntos y rectas notables del triángulo.
Entre las rectas notables más conocidas de un triángulo veremos las mediatrices, las medianas, las alturas y las bisectrices; Y, sobre sus puntos notablesasociados: el circuncentro, el baricentro, el ortocentro y el incentro y exincentros, respectivamente.4.1. Rectas notables: mediatrices, medianas, alturas y bisectrices
Mediatrices y circuncentro
Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.
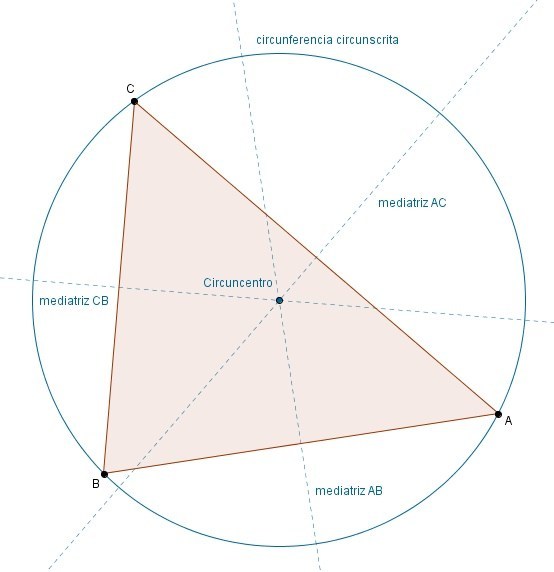
La mediatriz de un segmento cualquiera es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de los puntos extremos de dicho segmento. En el caso del lado de un triángulo es, por tanto, el lugar geométrico de los puntos que equidistan de los vértices de dicho lado.
Las tres mediatrices del triángulo (hay una por cada lado) se cortan en un punto que está, por tanto, a la misma distancia de los tres vértices del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. A esa circunferencia se la denomina circunferencia circunscrita, y al centro de la misma en el que se cortan las tres mediatrices circuncentro.
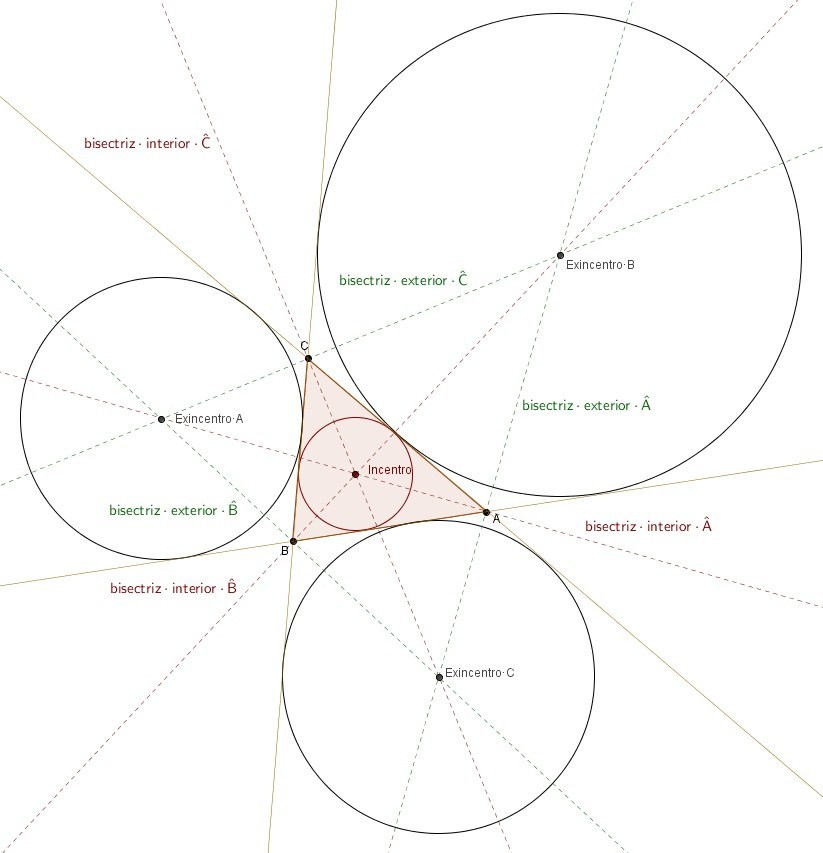
Bisectrices, incentro y exincentros
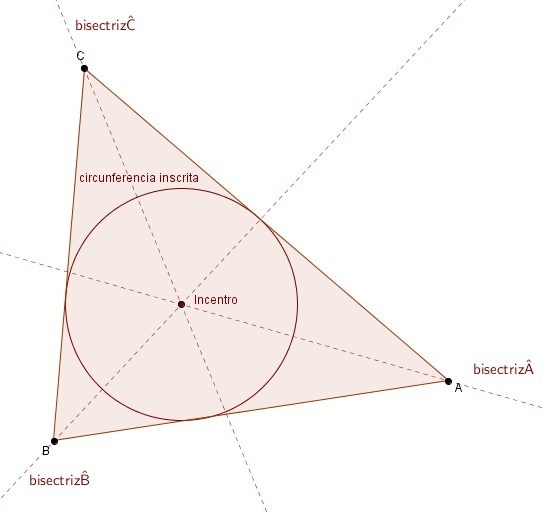
a bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.
Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.
Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.
Medianas y baricentro
Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.
Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.
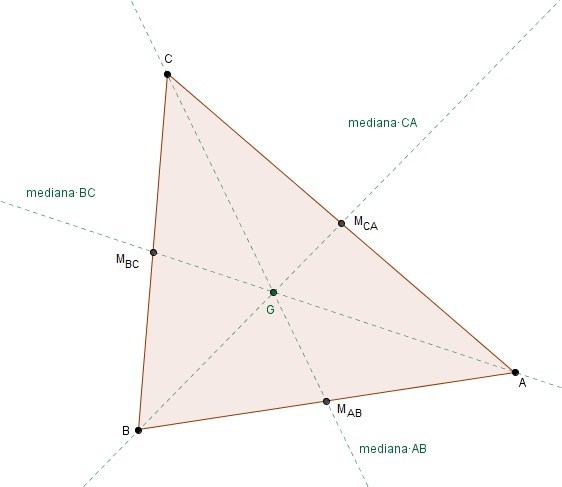
Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.
![]()
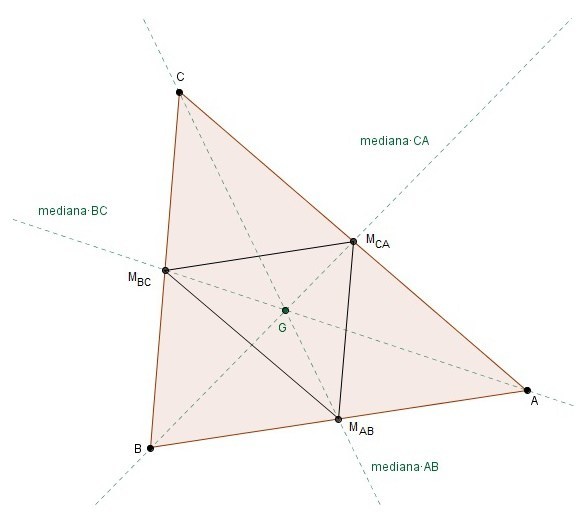
Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.
También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.
En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.
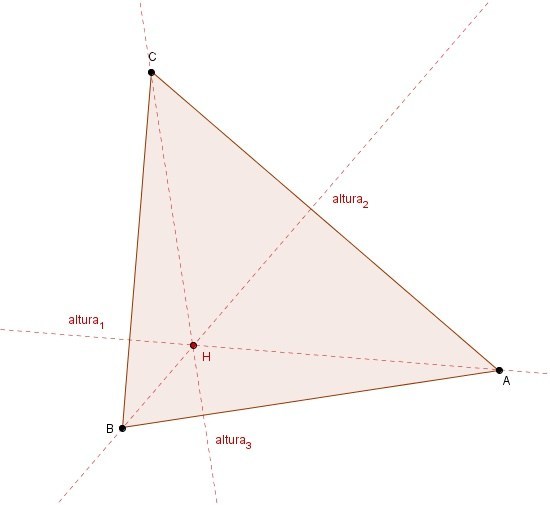
Alturas y ortocentro
Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.
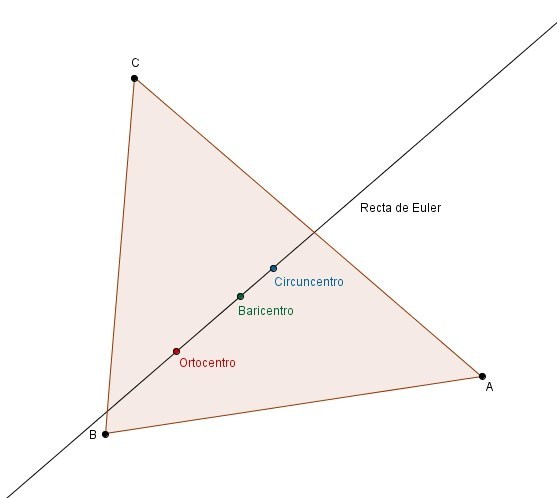
Recta de Euler
La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).
Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.
4.2. Rectas notables de un triángulo | Bisectriz, mediana, mediatriz y altura
4.3. Alturas de un triangulo y ortocentro | Todo tipo de triángulo
4.4. Bisectrices de un triangulo | Incentro
5. Teorema de Pitágoras en las culturas ancestrales.
Mucho antes de que Pitágoras (o alguno de sus discípulos) demostrara su famoso teorema, los babilonios, los indios y los egipcios conocían -y utilizaban eficazmente- las propiedades del triángulo de lados 3, 4 y 5, que se consideraba sagrado. Lo más notable de este triángulo es que el ángulo opuesto al lado mayor es recto, y no hace falta señalar la importancia del ángulo recto en todo tipo de mediciones y construcciones.

En el antiguo Egipto, el triángulo de proporciones 3-4-5 más utilizado en arquitectura y agrimensura era el de lados iguales a 15, 20 y 25 codos respectivamente (unos 7.5, 10 y 12.5 metros), llamado “triángulo isíaco” en honor a la diosa Isis, que ya se utilizó en la construcción de la pirámide de Kefrén, en el siglo XXVI a. C. Pero fueron los pitagóricos quienes, dos mil años después, demostraron el teorema y le dieron su conocida expresión canónica:
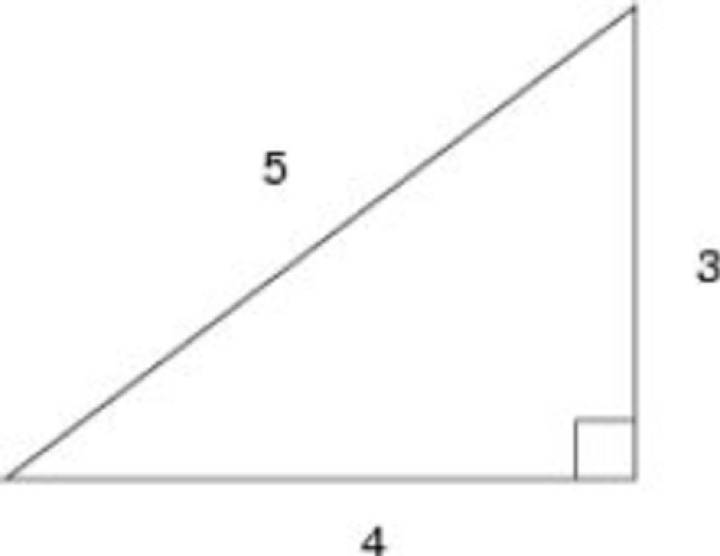
“En todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”.
El ángulo recto es un elemento fundamental de nuestro entorno físico, hasta el punto de que el gran arquitecto Le Corbusier lo denominó “nuestro pacto de solidaridad con la naturaleza” y le dedicó un extenso -e intenso- poema; he aquí un fragmento:
Erguido sobre el plano terrestre / de las cosas comprensibles, / contraes con la naturaleza un pacto / de solidaridad: es el ángulo recto. / De pie vertical ante la mar, / hete ahí sobre tus piernas
Desde el momento en que se irguieron sobre sus patas traseras, los primeros homínidos debieron cobrar plena conciencia del binomio horizontal-vertical, o lo que es lo mismo, de la perpendicularidad.
Es probable que las primeras demostraciones del teorema de Pitágoras fueran geométricas, ya que los pitagóricos lo veían como una relación de los cuadrados construidos sobre los tres lados del triángulo rectángulo más que como una ecuación algebraica. Una de las demostraciones más elegantes es la que ilustra la figura (que también se encuentra representada en algunos documentos chinos muy antiguos).
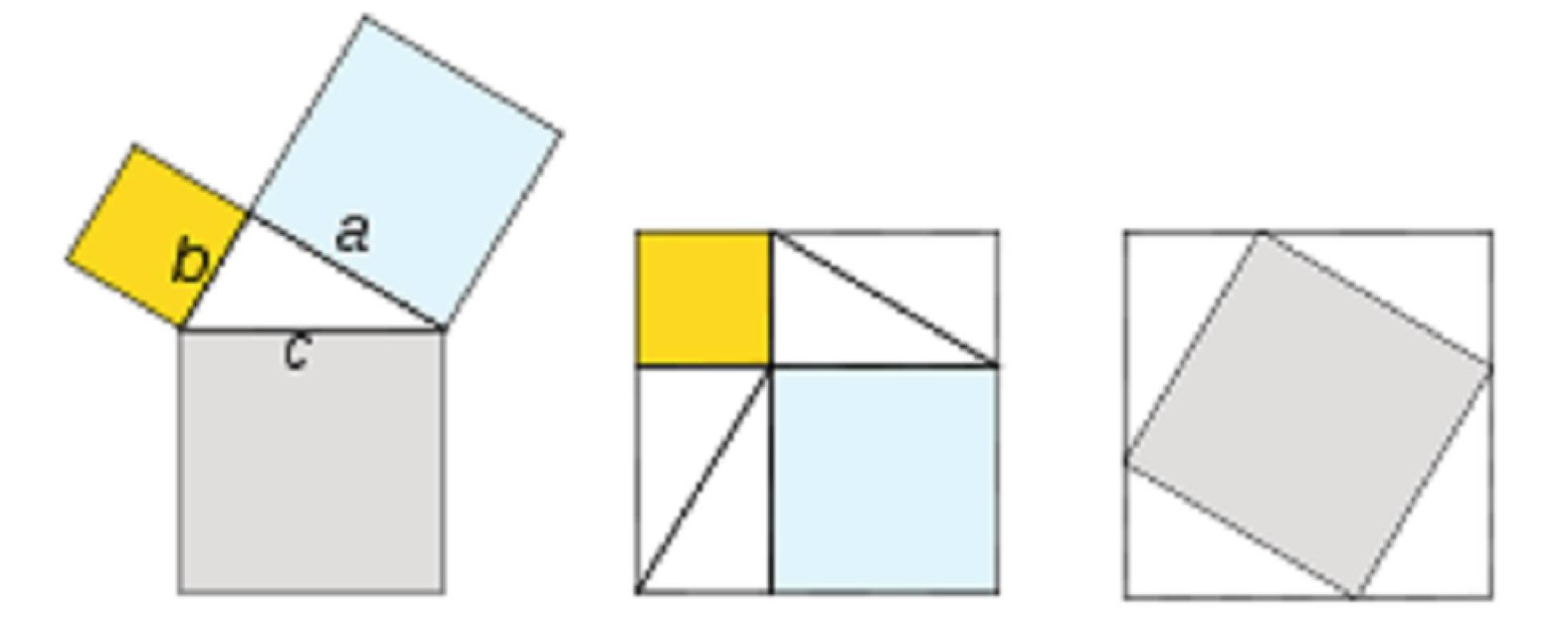
El cuadrado del centro y el de la derecha son iguales. El de la derecha está formado por el cuadrado de lado igual a la hipotenusa y cuatro triángulos iguales al original; el del centro, por dos cuadrados de lados iguales, respectivamente, a ambos catetos y cuatro triángulos iguales al original; por lo tanto, el área del cuadrado mayor es igual a la suma de las áreas de los dos menores, o lo que es lo mismo, a2 + b2 = c2.
La demostración que encontramos con frecuencia en los libros de geometría actuales (atribuida al propio Pitágoras) se basa en la semejanza de triángulos.
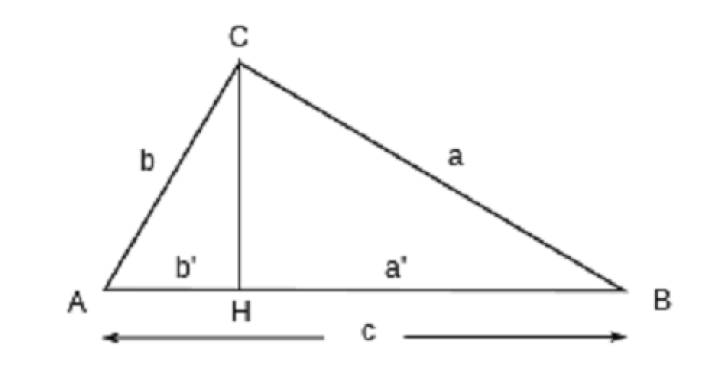
Los triángulos ABC y ACH son semejantes porque ambos son rectángulos y tienen en común el ángulo A, y por tanto sus lados son proporcionales, luego b’/b = b/c, de donde b2 = cb’. También son semejantes ABC y BCH, pues tienen en común el ángulo B, luego a’/a = a/c, de donde a2 = ca’. Sumando ambas igualdades: a2 + b2 = ca’ + cb’ = c(a’ + b’) = c2.
5.1. Teorema de Pitágoras (Biblioteca de KUAA)
NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (LIBRO PROPORCIONADO POR LA BIBLIOTECA DE KUAA)
ESCUELA DE MATEMÁTICAS UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN
La trigonometría se inició con el estudio de las relaciones entre los lados y ángulos de un triángulo rectángulo. Una de las relaciones ya conocidas es la que existe entre la
longitud de los catetos y la de la hipotenusa. Recordemos el teorema que describe dicha relación.
Teorema de Pitágoras.
En todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos.
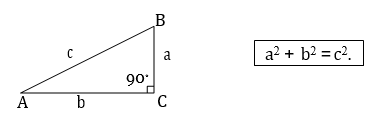
Ejemplo
En un triángulo rectángulo uno de sus catetos mide 5 cm y la hipotenusa 13 cm. Encontremos la longitud del otro cateto.
Solución
Aplicamos el teorema de Pitágoras. Representemos por c la longitud de la hipotenusa y las longitudes de los catetos por a y b.
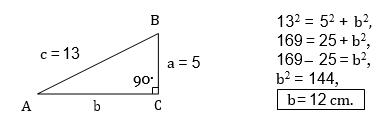
5.2. Demostración gráfica y analítica del Teorema de Pitágoras
El teorema de Pitágoras
En primer lugar deberíamos recordar un par de ideas:
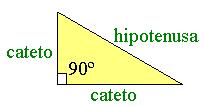
- Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
- En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos
¿Qué es el teorema de Pitágoras?
Tenemos una página que explica el Teorema de Pitágoras, pero aquí tienes un breve resumen:
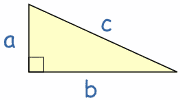
El teorema de Pitágoras dice que en un triángulo rectángulo, el cuadrado de a (a²) más el cuadrado de b (b²) es igual el cuadrado de c (c²):
a2 + b2 = c2
Demostración del teorema de Pitágoras usando álgebra
Podemos ver que a2 + b2 = c2 usando el Álgebra
Mira este diagrama... tiene dentro un triángulo "abc" (en realidad tiene cuatro):
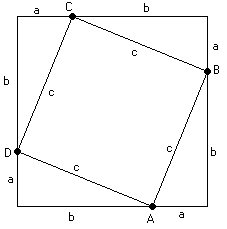
Es un gran cuadrado, cada lado mide a+b, así que el área es:
A = (a+b)(a+b)
Ahora sumamos las áreas de los trozos más pequeños:
Y hay cuatro triángulos, cada uno con área A =½ab
Así que los cuatro juntos son A = 4(½ab) = 2ab
Si sumamos el cuadrado inclinado y los 4 triángulos da: A = c²+2ab
El área del cuadrado grande es igual al área del cuadrado inclinado y los 4 triángulos. Esto lo escribimos así:
(a+b)(a+b) = c²+2ab
Ahora, vamos a operar a ver si nos sale el teorema de Pitágoras:
Empezamos con: (a+b)(a+b) = c²+2ab
Desarrollamos (a+b)(a+b): a²+2ab+b² = c²+2ab
Restamos "2ab" de los dos lados: a²+b² = c²

5.3. Teorema de pitágoras │ demostración
5.4. Teorema de Pitágoras Fórmula, Demostración y Ejemplos
6. Elementos de la Circunferencia y el Círculo: Radio, Diámetro, Cuerda, Arco circunferencial, Sector circular y Segmento circular.
La circunferencia
Una circunferencia es una línea curva, cerrada y plana cuyos puntos están a la misma distancia de un punto interior llamado centro.
La circunferencia es plana porque todos sus puntos están en un mismo plano.
Elementos de la circunferencia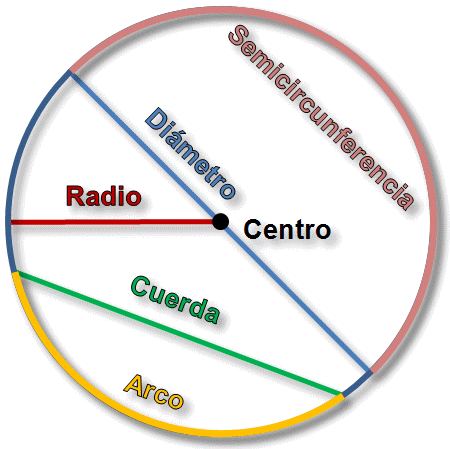
- Centro punto del interior de la circunferencia tal que la distancia desde él a cualquier punto de la circunferencia es la misma.
- Radio es el segmento que une el centro con cualquier punto de la circunferencia.
- Diámetro es el segmento que tiene por extremos dos puntos de la circunferencia y que pasa por el centro. El diámetro es el doble del radio. D = 2·R
- Cuerda es el segmento que une dos puntos cuales quiera de la circunferencia. La cuerda mayor de una circunferencia es el diámetro.
- Arco parte de la circunferencia comprendida entre dos puntos.
- Semicircunferencia es cada una de las partes en que un diámetro divide a una circunferencia, es decir, media circunferencia.
El círculo
Elementos del círculo
El círculo es la superficie del plano limitada por la circunferencia.
Es decir, está formado por todos los puntos de la circunferencia y todos los puntos del plano en su interior.
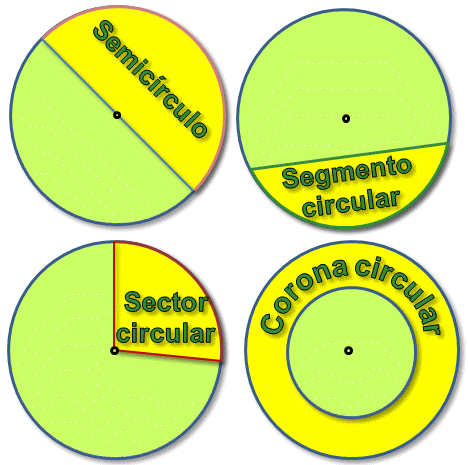
Elementos del círculo:
- Semicírculo: una de las dos partes iguales que delimita un diámetro.
- Sector circular: es la parte del círculo comprendida entre dos radios y su arco.
- Segmento circular: es la parte del limitada por un arco y su cuerda.
- Corona circular: es el espacio comprendido entre dos circunferencias con el mismo centro y distinto radio (concéntricas)
Posición de una recta con respecto a una circunferencia.
Decimos que una recta puede situarse en esta tres posiciones respecto a una circunferencia:
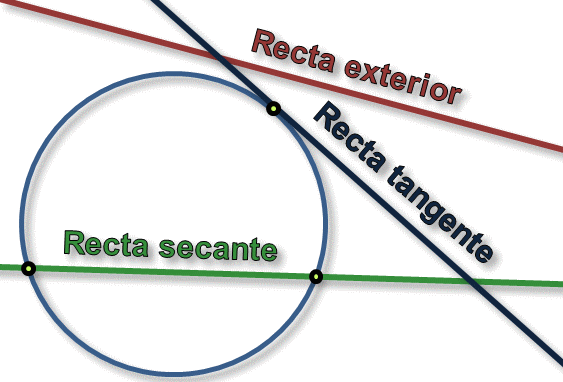
- Recta exterior: es aquella que no toca en ningún punto a la circunferencia.
- Recta tangente: es aquella que toca en un solo punto a la circunferencia.
- Recta secante: es aquella que toca en dos puntos a la circunferencia.
Posiciones relativas de dos circunferencias:
Según los puntos que comparten diferenciamos:
- Exteriores: no comparten ningún punto en común.
- Interiores: con comparten ningún punto en común pero una está dentro de la otra.
- Tangentes exteriores: comparten un punto en común pero ninguna está incluida en la otra.
- Tangentes interiores: comparten un punto en común y una está dentro de la otra.
- Secantes: cuando comparten dos puntos en común (se cortan en dos puntos)
- Concéntricas: es un caso especial de circunferencias interiores que tienen el mismo centro.
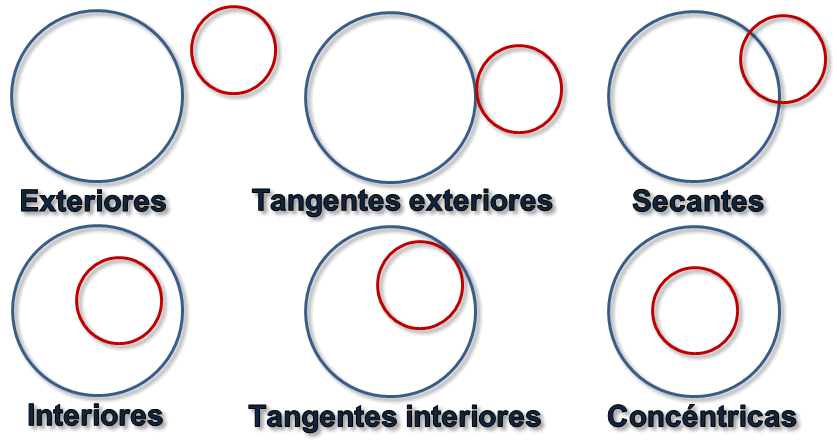
6.1. Circunferencia y círculo. Elementos
7. El valor de “π” y los saberes matemáticos ancestrales e interculturales.
El nombre actual del número es el mismo que el de la letra griega ‘π’, inicial de las palabras 'periferia' y 'perímetro', y fue usado inicialmente por William Oughtred (1574-1660), aunque lo popularizó Leonhard Euler (1707-1783), ambos matemáticos europeos. Antes, el número pi había sido conocido como 'constante de Ludolph' (en honor al matemático Ludolph Van Ceulen) o como 'constante de Arquímedes', pues fue este último el primero en encontrar su valor.

El hallazgo de Arquemedes
Fue en el siglo III antes de Cristo, cuando el físico griego logró determinar el valor de pi, utilizando polígonos para afinar el cálculo. Su aproximación tuvo un error de solo el 0.024% y el 0.040% sobre el valor real.
Pero si bien fue Arquímedes el primero en proponer un valor, a través de los años diversos matemáticos y científicos siguieron en la búsqueda del valor exacto de pi.
Así, Claudio Ptolomeo (en el siglo II) mejoró la aproximación de Arquímedes, y estableció el valor de 3,14166 para pi, empleando un polígono de 120 lados. A finales del siglo V, el matemático y astrónomo chino Zu Chongzhi dio un paso más, atribuyéndole un valor de 3,1415927, resultado que no fue mejorado hasta el siglo XV.
Tras siglos de cálculos, la llegada de la informática y las computadoras cambiaron los parámetros: el cálculo se disparó y se han ido añadiendo decimales que, hasta la fecha, ya suman hasta los 12,1 billones.
"La historia de PI refleja el más influyente, el más grave y, a veces, el tonto aspecto de las matemáticas. Una sorprendente cantidad de los más importantes matemáticos han contribuido a su evolución, directa o indirecta.
Pi es uno de los pocos conceptos en las matemáticas, cuya mención evoca una respuesta de reconocimiento y el interés en aquellos que no se traten profesionalmente con el tema. Ha sido una parte de la cultura humana y la imaginación, estudiado durante más de veinticinco siglos.
El cálculo de Pi es prácticamente el único tema de los más antiguos estratos de las matemáticas que es aún de gran interés para la investigación matemática moderna." (Traducción tomada de la introducción a "Pi: A Source Book", por L. Berggren, J. Borwein y P. Borwein.)

¿Que es el número PI?
π (pi) es la relación entre el perímetro de una circunferencia y la longitud de su diámetro, no es un número exacto, pertenece al conjunto de números irracionales, es decir, que tiene infinitos números decimales.
Definición de Pi
π (pi) es un número irracional, cociente entre la longitud de la circunferencia y la longitud de su diámetro. Se emplea frecuentemente en matemática, física e ingeniería. El valor numérico de π truncado a sus diez primeras posiciones decimales, es el siguiente: 3,14159 26535...