LA FORMA, EL NÚMERO Y LA RELACIÓN CON EL ENTORNO NATURAL Y CULTURAL
a
4. Puntos y Rectas notables de triángulos.
4.1. Rectas notables: mediatrices, medianas, alturas y bisectrices
Mediatrices y circuncentro
Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.
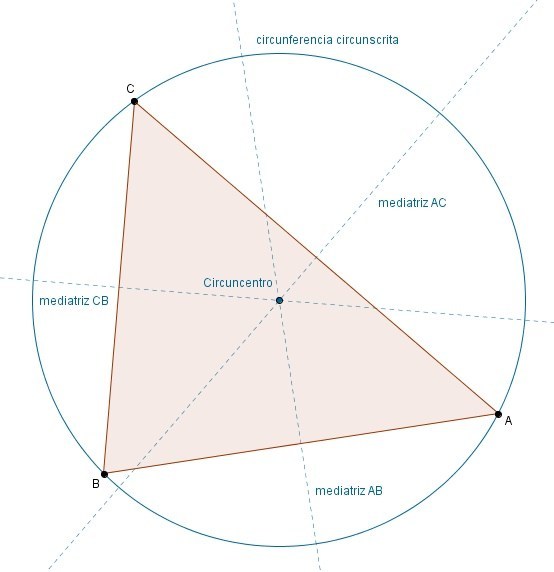
La mediatriz de un segmento cualquiera es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de los puntos extremos de dicho segmento. En el caso del lado de un triángulo es, por tanto, el lugar geométrico de los puntos que equidistan de los vértices de dicho lado.
Las tres mediatrices del triángulo (hay una por cada lado) se cortan en un punto que está, por tanto, a la misma distancia de los tres vértices del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. A esa circunferencia se la denomina circunferencia circunscrita, y al centro de la misma en el que se cortan las tres mediatrices circuncentro.
Bisectrices, incentro y exincentros
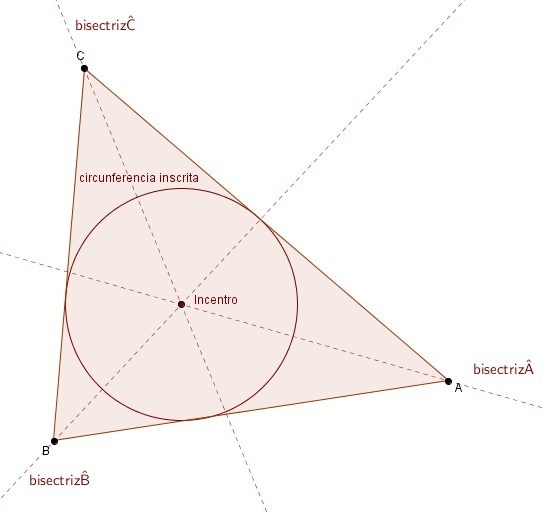
a bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.
Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.
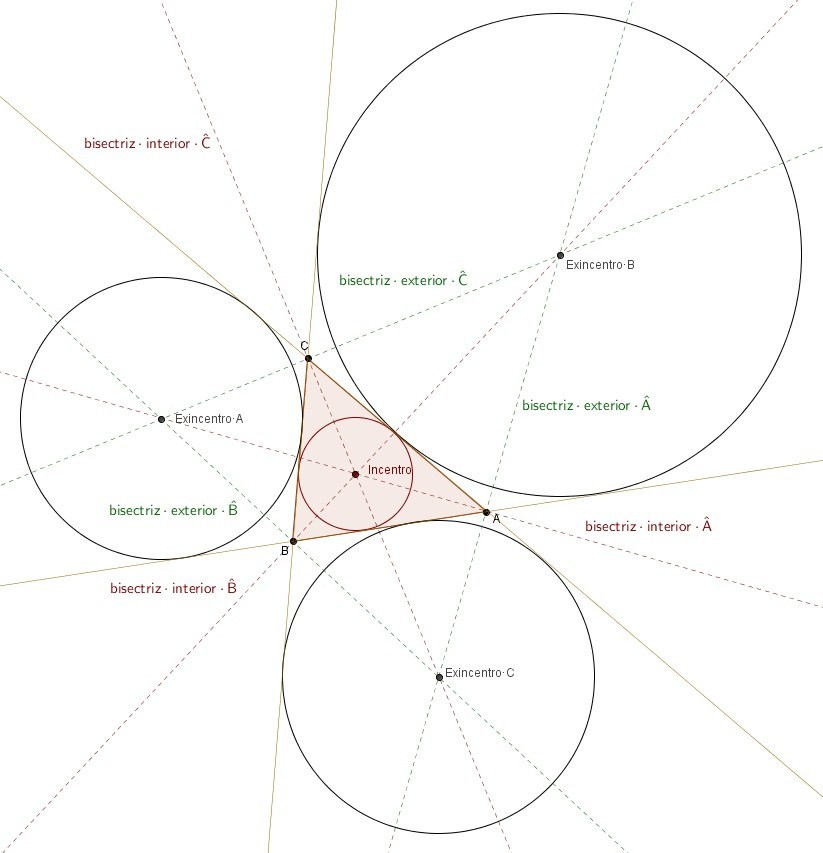
Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.
Medianas y baricentro
Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.
Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.
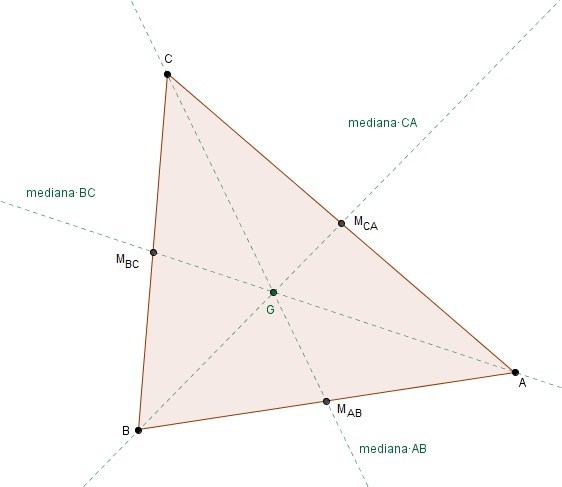
Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.
![]()
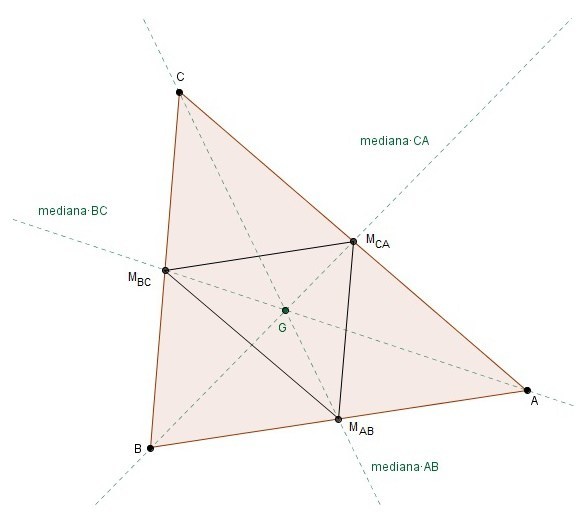
Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.
También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.
En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.
Alturas y ortocentro
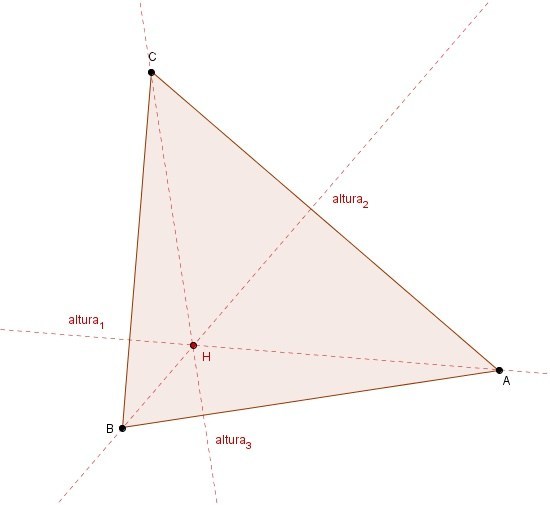
Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.
Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.
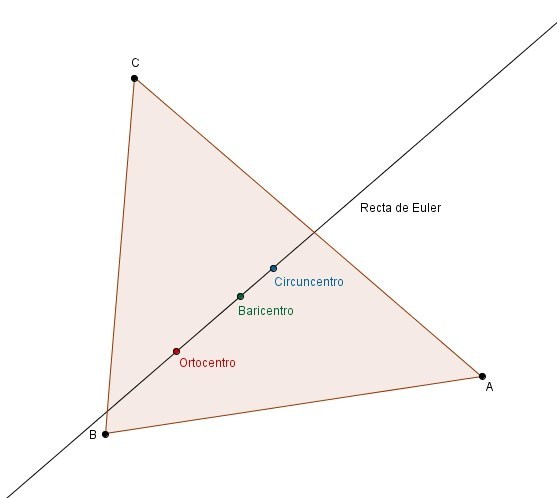
Recta de Euler
La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).
Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.