TRIGONOMETRÍA, TECNOLOGÍA Y PRODUCCIÓN
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Matemáticas |
| Libro: | TRIGONOMETRÍA, TECNOLOGÍA Y PRODUCCIÓN |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 11:15 |
Tabla de Contenidos
- 1. Nociones de trigonometría en el entorno natural y tecnológico.
- 2. Medida angular y determinación de un punto en el círculo unitario.
- 3. Funciones trigonométricas
- 4. Resolución de triángulos rectángulos y oblicuángulos (ley de senos y de los cosenos).
- 5. Calculo del área de un triángulo cualquiera en función de los lados y a través de la fórmula de Herón.
- 6. Aplicaciones de la trigonometría en actividades productivas diversas.
1. Nociones de trigonometría en el entorno natural y tecnológico.
La trigonometría es una rama de las matemáticas de antiguo
origen, cuyo significado etimológico es “la medición de los triángulos”.
La trigonometría en principio es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Para esto se vale de las razones trigonométricas, las cuales son utilizadas frecuentemente en cálculos técnicos. En términos generales, la trigonometría es el estudio de las funciones seno, coseno, tangente, cotangente, secante y cosecante.
Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.
Ver información mas detallada sobre nociones trigonométricas.....https://ue.aprendiendomas.com.bo/pluginfile.php/525/mod_book/chapter/2984/nociones%20trigonom%C3%A9tricas%20pdf.pdf
Video completo de nociones trigonométricas
2. Medida angular y determinación de un punto en el círculo unitario.
¿Qué es la definición de las funciones trigonométricas en el círculo unitario?

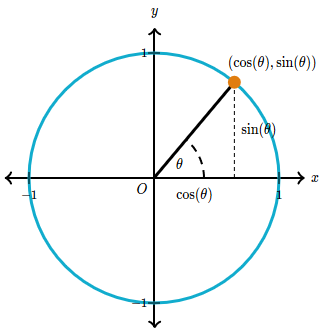
Las demás funciones trigonométricas pueden evaluarse a partir des su relación con seno y coseno.
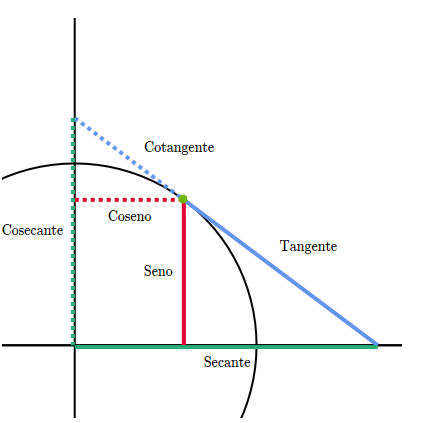
Apéndice: todas las razones trigonométricas en el círculo unitario
Utiliza el punto movible para ver cómo cambian las longitudes de las razones de acuerdo al ángulo.
3. Funciones trigonométricas
Las funciones trigonométricas son razones trigonométricas, es decir la división entre dos lados de un triángulo rectángulo respecto a sus ángulos, estas funciones surgieron al estudiar el triángulo rectángulo y observar que los cocientes entre las longitudes de dos de sus lados sólo dependen del valor de los ángulos del triángulo.
Las funciones trigonométricas tienen varias aplicaciones en astronomía, matemáticas, física, en planos y en algunos otros fenómenos.
¿Qué son las funciones trigonométricas?
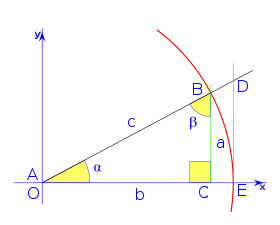
Para definir las funciones trigonométricas del ángulo:![]() del vértice A, se parte de un triángulo rectángulo. El nombre de los lados de este triángulo rectángulo son:
del vértice A, se parte de un triángulo rectángulo. El nombre de los lados de este triángulo rectángulo son:
- La hipotenusa (c) es el lado opuesto al ángulo recto, o el lado más grande.
- El cateto opuesto (a) es el lado opuesto al ángulo
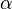
- El cateto adyacente (b) es el lado adyacente al ángulo
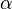
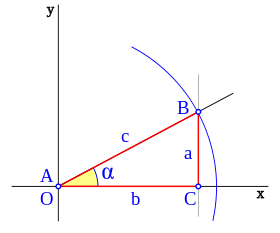

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:
sen α = opuesto/hipotenusa.
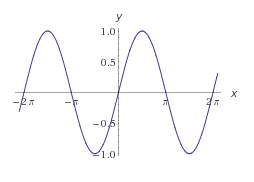
2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:
cos α = adyacente/hipotenusa
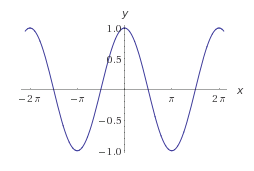
3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:
tan α = opuesto/adyacente
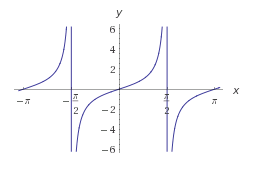
4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:
cot α = adyacente/opuesto
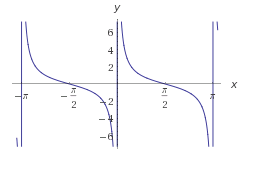
5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:
sec α = hipotenusa/adyacente
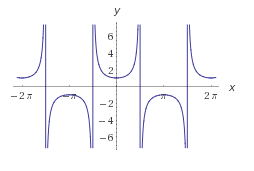
6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:
csc α = hipotenusa/opuesto
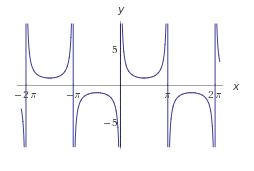
En la siguiente tabla podemos ver los valores de las funciones trigonométricas con diferentes ángulos (ind significa que no se puede calcular el valor de la función).
Ver video sobre funciones trigonométricas
3.1. Teorema de Pitágoras en la trigonometría en el plano y el espacio.
El teorema de Pitágoras
En primer lugar deberíamos recordar un par de
ideas:
- Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
- En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
Teorema de Pitágoras.- En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
DEMOSTRACIÓN
El área de este cuadrado será (b+c)2.
3.2. Razones trigonométricas y sus propiedades
Razones trigonométricas
Seno
El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa.
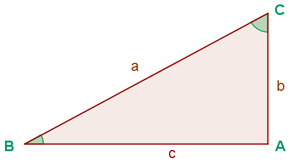
Coseno
El coseno del ángulo B es la razón entre el cateto contiguo al ángulo y la hipotenusa.
Se denota por cos B.
![]()
Tangente
La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.
Se denota por tg B.
![]()
Cosecante
La cosecante del ángulo B es la razón inversa del seno de B.
Se denota por cosec B.
Secante
La secante del ángulo B es la razón inversa del coseno de B.
Se denota por sec B.
![]()
Cotangente
La cotangente del ángulo B es la razón inversa de la tangente de B.
Se denota por cotg B.
![]()
Propiedades de las razones trigonométricas
1.- El valor del seno y del coseno siempre estará comprendido entre 0 y 1
(nunca puede ser mayor que 1, ya que se trata del cociente entre un
cateto y la hipotenusa, y el cateto nunca puede ser mayor que la
hipotenusa).
2.- La suma del cuadrado del seno y del cuadrado del coseno de un ángulo es igual a 1.
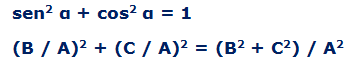
Pero sabemos por el teorema de Pitágoras que: ![]()
Luego:
![]()
3.- El seno de un ángulo es igual al coseno de su ángulo complementario
(aquel que sumado al primero da 90°), mientras que el coseno de un
ángulo es igual al seno de su complementario.
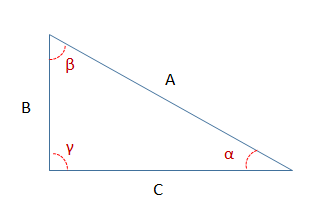
Hemos señalado en este triángulo sus 3 ángulos: el ángulo γ es el ángulo recto (90°), luego los otros dos ángulos α y β son complementarios, ya que necesariamente tienen que sumar 90° (los 3 ángulos tienen que sumar 180°).
a) Equivalencia entre el seno de α y el coseno de su complementario β:
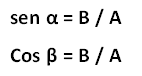
Por lo tanto: ![]()
b) Equivalencia entre el coseno de α y el seno de su complementario β:
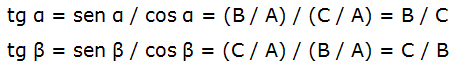
Luego:
![]()
Ver más sobre razones trigonométricas y sus propiedades
3.3. Relaciones trigonométricas fundamentales.
Relaciones Trigonométricas Fundamentales
Sigue el avance trigonométrico y hasta ahora nos hemos defendido bastante bien. Claro que hemos ido estudiando meticulosamente la materia ya que el profe Danny nos advirtió que si no captábamos el principio de la trigonometria, después daríamos la hora en las clases y, por supuesto, en las pruebas (¿cierto Cynthia?).
Hoy aprenderemos que existen relaciones trigonométricas que serán fundamentales en el desarrollo de las diversas unidades de nuestro curso. Para eso vamos a trabajar con la figura siguiente, para que basados en ella demostremos las relaciones que más abajo se indican.
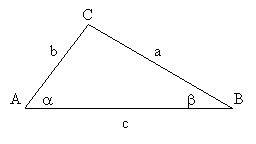
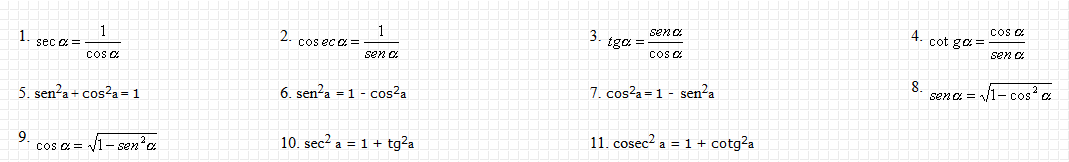
¡Apréndelas!, las tendrás que utilizar siempre, especialmente en las identidades y ecuaciones trigonométricas que estudiaremos más adelante.
Y ahora a demostrar cada una de ellas, basándote en el triángulo anteriormente dado. ¡A trabajar!
(Aquí te damos algunas demostraciones como pauta para que tú hagas todas las demás)
1. Por demostrar ![]()
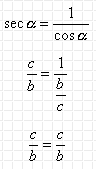
queda entonces demostrado.
2. Por demostrar ![]()
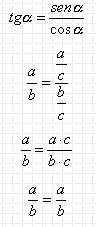

3.4. Relaciones de las funciones trigonométricas para ángulos notables de un triángulo rectángulo.
Funciones trigonométricas de ángulos notables
En la actualidad para obtener el valor de una razón trigonométrica a partir de un ángulo dado, simplemente se utiliza una calculadora en la cual se introduce el valor del ángulo dado y se evalúa en la relación trigonométrica requerida. Los valores de estas razones también se pueden obtener utilizando triángulos rectángulos, cuyos ángulos serán a los que se les quiere encontrar sus razones trigonométricas. En ocasiones este método es muy engorroso, ya que para crear los triángulos se deben realizar bastantes operaciones. Sin embargo, existen ángulos en los que es muy fácil; a estos ángulos se les conoce como ángulos notables.
En las matemáticas y específicamente en la trigonometría, la palabra “notable” se utiliza para referirnos a procesos o valores que están bien definidos o muy comunes, y por ende, se reconocen y memorizan fácilmente. En este sentido, los ángulos notables son aquellos que tienen valores que aparecen muy seguido en la vida cotidiana. Estos ángulos son los de 30°, 45° y 60° y, en segundo lugar, los ángulos de 0°, 90°, 180°, 270° y 360°. Estos últimos, aunque no están definidos como 'notables', también son muy comunes.
Para los 3 ángulos notables podemos encontrar las razones trigonométricas —seno, coseno, tangente, cotangente, secante y cosecante— sin conocer las medidas exactas de los triángulos que los contienen, pues estos ángulos están contenidos en dos triángulos muy especiales e importantes en geometría, a saber: los triángulos isósceles rectángulos y los triángulos equiláteros.
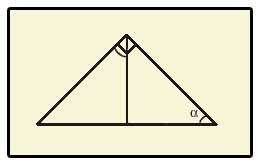
En geometría, un triángulo es un polígono de tres lados que se puede construir a partir de la unión de tres segmentos que se tocan en sus extremos. Cada uno de los puntos de unión entre dos segmentos se llama vértice y la abertura que hay entre cada par de segmentos se llama ángulo. Un triángulo tiene tres vértices y tres ángulos. Finalmente, una de las propiedades de los triángulos que nos interesa es que la suma de los ángulos de un triángulo es 180°.
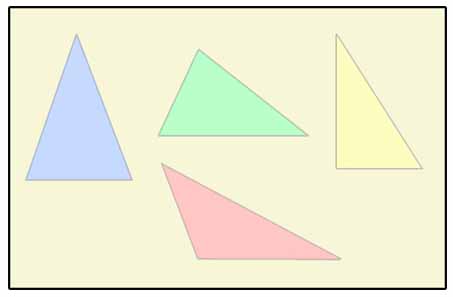
Existen varias formas para clasificar los triángulos.
- Una de ellas es a través de la amplitud de sus ángulos. Un triángulo es rectángulo cuando uno de sus ángulos es recto (es decir: mide 90°); dicho ángulo es delimitado por un par de lados que se conocen como catetos, mientras que el lado opuesto al ángulo recto recibe el nombre de hipotenusa. Un triángulo es acutángulo cuando sus tres ángulos interiores son agudos (miden menos de 90°) y obtusángulo cuando uno de sus ángulos es obtuso (mayor que 90°).
- Otra manera de clasificar los triángulos es por la longitud de sus lados. En esta clasificación, los triángulos son equiláteros cuando sus tres lados tienen la misma longitud; en este caso, los tres ángulos también son iguales. Un triángulo es isósceles cuando dos de sus lados tienen la misma longitud y de igual forma dos de sus ángulos son iguales. Finalmente se denominan escalenos aquellos triángulos cuyos tres lados tienen diferente longitud.
Obtención de las funciones trigonométricas para ángulos de 30° y 60°
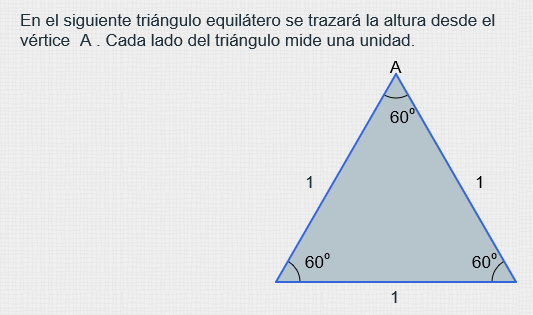
Antes de encontrar el valor para las funciones trigonométricas de los ángulos notables de 30° y 60°, vamos a originar dichos ángulos a partir de un triángulo equilátero. El triángulo equilátero que requerimos es aquel cuyos tres lados tienen una longitud de 1 unidad; además, cada uno de sus ángulos mide 60° (como siempre es el caso en un triángulo equilátero).
Ya que se tiene el triángulo equilátero, de éste se formarán dos triángulos a partir de su altura. Estos nuevos triángulos estarán compuestos por un ángulo de 30°
Y 60°. Finalmente para obtener el valor de una relación trigonométrica, ya sea para 30° o 60°
, sólo hay que utilizar sus definiciones.
En el siguiente recurso interactivo observa paso a paso la obtención de las razones trigonométricas para el ángulo de 60°. Nota además que de inmediato y de forma análoga se obtienen también las razones trigonométricas para el ángulo de 30°.
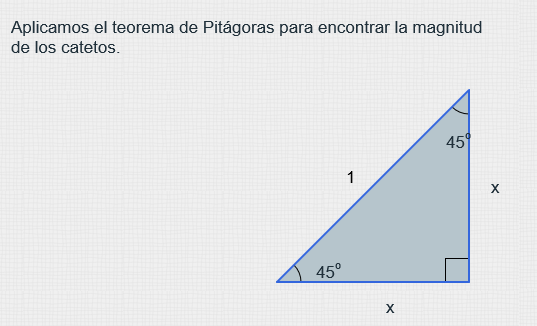
Obtención de las funciones trigonométricas para un ángulo de 45°
Para encontrar los valores de las funciones trigonométricas del ángulo notable de 45° utilizaremos un triángulo rectángulo isósceles. En dicho triángulo, se cumple que dos de sus lados tienen la misma longitud, digamos x
. Además, como el triángulo es rectángulo, uno de los ángulos es de 90°, por lo que los otros dos medirán 45° (recuerda que los triángulos isósceles siempre tienen dos ángulos idénticos).
Por conveniencia asignaremos a la hipotenusa el valor de 1
Unidad. A continuación podemos utilizar el teorema de Pitágoras para encontrar la longitud de sus catetos. Finalmente, para obtener el valor de las funciones trigonométricas solo hay que utilizar sus definiciones.
En el siguiente espacio interactivo observa paso a paso la obtención de las razones trigonométricas para el ángulo de 45°.
Múltiplos de ángulos notables
A partir de que ya obtuvimos los valores de las funciones trigonométricas de los ángulos notables de 30°, 45° y 60°, podemos obtener también los valores para funciones que representan los múltiplos de dichos ángulos. Para encontrar estas razones trigonométricas, vamos a utilizar los valores que ya hemos encontrado en un triángulo rectángulo.
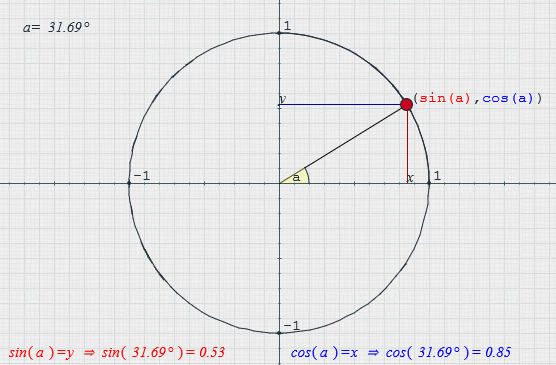
Estas definiciones las plantearemos tomando como base la circunferencia unitaria (es decir: ), una circunferencia de radio 1
Por lo que es útil recordar algunas definiciones:
El seno se define como la razón entre el valor de la coordenada Y del segmento que forma el ángulo con el eje X y la longitud de dicho segmento. En la circunferencia unitaria, el segmento es el radio y mide 1
Unidad, por lo que el seno es igual al valor de la coordenada Y:
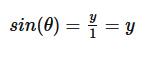
La relación inversa del seno es y se define como:
![]()
El coseno es la razón entre el valor de la coordenada X del segmento que forma el ángulo con el eje X y la longitud del segmento. De igual forma que para el seno, como es una circunferencia unitaria, el coseno equivale a la coordenada X:
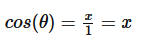
La relación inversa del coseno es y se define como:
![]()
MÁS SOBRE FUNCIONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO
4. Resolución de triángulos rectángulos y oblicuángulos (ley de senos y de los cosenos).
5. Calculo del área de un triángulo cualquiera en función de los lados y a través de la fórmula de Herón.
6. Aplicaciones de la trigonometría en actividades productivas diversas.
Las aplicaciones de la trigonometría en la ciencia y en la vida cotidiana
1- Aplicaciones en la astronomía
La trigonometría se usa en la astronomía para calcular la distancia del planeta Tierra al Sol, a la Luna, el radio de la Tierra y también para medir la distancia entre los planetas.
Para realizar esas mediciones se valen de la triangulación, la cual consiste en tomar distintos puntos de lo que se desea medir y considerar cada uno como vértices de triángulos; de ahí se saca la distancia entre un punto y otro.
Los egipcios establecieron la medida de los ángulos en grados, minutos y segundos, y lo utilizaron en la astronomía.
2- Aplicaciones en la arquitectura
La aplicación de la trigonometría en la arquitectura es algo que nunca debe faltar. De su uso depende la creación de los planos y su posterior ejecución.
La creación de una casa o de un edificio debe seguir unos parámetros específicos. Por ejemplo: se debe medir cada ángulo de todas las paredes y las columnas con el objeto de evitar alguna deformidad que con el tiempo pueda hacer que el edificio se derrumbe.
Un ejemplo claro del uso de la trigonometría en la arquitectura se observa en las pirámides egipcias y en las construcciones realizadas por las civilizaciones que habitaban el continente americano antes de la llegada de los españoles.
Debido a la aplicación de la trigonometría es que esas construcciones siguen casi intactas con el paso del tiempo.
3- Aplicaciones en la navegación
La trigonometría fue utilizada en la navegación durante muchos años y para ello crearon lo que hoy se conoce como sextante, instrumento con el que se podía medir la distancia triangulando con el Sol o las estrellas.
El sextante era utilizado de la siguiente manera: se debía determinar la altura angular del Sol (o de las estrellas o de cualquier astro que pueda servir como punto de referencia) por encima del horizonte.
Posteriormente se podrían realizar cálculos matemáticos para determinar el punto en el que se encuentra el observador, es decir, la persona que está usando el sextante.
Conociendo dos puntos de una costa o una isla, el sextante también podía ser utilizado para medir la distancia en la que se encontraban los barcos de la costa.
El sextante era el encargado de orientar a los capitanes de los barcos. En la actualidad el sextante ha sido reemplazo por los sistemas satelitales. Estos también se valen del uso de la trigonometría.
4- Aplicaciones en la geografía
En la geografía la trigonometría se usa para el cálculo de las distancias en un mapa; es decir, se vale de los paralelos y los meridianos para poder calcular la longitud.
5- Aplicaciones en los videojuegos
La trigonometría se usa para la programación de videojuegos. Por esto, todo lo que se presenta en la pantalla requiere de la trigonometría.
6- Aplicaciones en la ingeniería civil
Un ejemplo del uso de la trigonometría en la ingeniería civil se observa mediante la construcción de puentes, carretera, edificios y en el trazo de levantamiento de terrenos, entre otros.
7- Aplicaciones en la ingeniería mecánica
La trigonometría se usa en la ingeniería mecánica para el diseño y medición de piezas en series. También se usa para proyectar fuerzas.
8- Aplicaciones en la ingeniería electrónica
La trigonometría se usa en la ingeniería electrónica para identificar el comportamiento de series y de señales.
La trigonometría ayuda a establecer conexiones y ubicar posiciones que favorezcan el proceso de distribución de la energía eléctrica.
9- Aplicaciones en el billar
La trigonometría es aplicada en este juego de mesa. Con base en el choque entre las bolas, hace que cada una de vaya en una dirección en particular creando unos ángulos específicos.
Estos ángulos son usados por cada jugador para determinar cuál será su siguiente movimiento.
10- Aplicaciones en la física
Para medir la trayectoria de un objeto se usa la trigonometría. Por ejemplo: cuando en un partido de fútbol se quiere hacer un pase aéreo es necesario buscar un ángulo y tener bien definido el punto hacia donde va dirigido.
Tomando en cuenta todos estos puntos se puede calcular la trayectoria del balón. Esto también puede ser aplicado para medir la trayectoria de un proyectil, un cohete, entre otros elementos.
11- Aplicaciones en la medicina
La trigonometría se aplica en la medicina para poder leer los electrocardiogramas, examen que registra gráficamente la actividad eléctrica del corazón en función del tiempo.
En estos estudios aparecen funciones del seno y el coseno. De acuerdo a cómo van apareciendo se les va otorgando una letra que le da significada a la onda. Esto permite que los médicos lo puedan leer y dar un diagnóstico oportuno.
Más información sobre aplicación de la trigonometría en la vida real y cotidiana