LENGUAJE ALGEBRAICO Y SU VALOR EN LA DIVERSIDAD CULTURAL
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Matemáticas |
| Libro: | LENGUAJE ALGEBRAICO Y SU VALOR EN LA DIVERSIDAD CULTURAL |
| Impreso por: | Invitado |
| Fecha: | jueves, 30 de enero de 2025, 23:57 |
Tabla de Contenidos
1. Propiedades algebraicas
Propiedades algebraicas de la suma y el producto

Consecuencias:
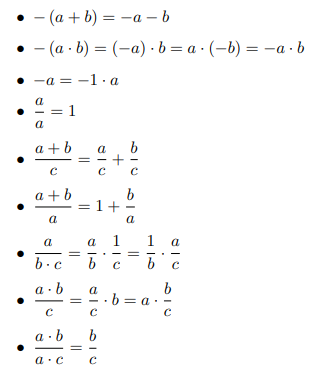
1.1. Propiedades algebraicas
1.2. Operaciones algebraicas combinadas.
OPERACIONES COMBINADAS
Las operaciones combinadas son aquellas en las que aparecen varias operaciones aritméticas para resolver.
Para obtener el resultado correcto deben seguirse las siguientes reglas:
Primero se deben separar los terminos y luego resolver cada uno de ellos.
Se resuelven las operaciones encerradas entre paréntesis, corchetes y llaves en el siguiente orden:
1) Potenciación y radicación
2) Multiplicación y división
3) Suma y resta
Se resuelven las sumas y las restas que separan los términos.

• La realización de este tipo de cálculos tiene sentido en dos casos: a) para expresar o llevar a cabo cálculos numéricos; y b) para resolver ecuaciones o problemas diversos. Un ejemplo del primer caso es el siguiente: el producto de dos binomios de la forma (x + a) (x – a) se puede expresar como:
• (x + a)(x - a) = x2 – ax + ax – a2 = x2– a2
EXPRESIONES ALGEBRAICAS
Definición.-Dentro del proceso de solución de un ejercicio, problema o exposición de una teoría, un símbolo (generalmente una letra) que se usa para representar un número real arbitrario se llama variable real.
Término algebraico
Es el producto y/o división de una o más variables (factor literal) y un coeficiente o factor numérico.
Por ejemplo:
![]() En este término algebraico, tenemos que 3 es el factor numérico y
En este término algebraico, tenemos que 3 es el factor numérico y![]() el coeficiente literal.
el coeficiente literal.
En este término algebraico, tenemos que -1 es el factor numérico y ab
el coeficiente literal.
Expresión algebraica
Es el resultado de combinar uno o más términos algebraicos mediante las operaciones de adición y/o sustracción.
Por ejemplo:
![]()
Cuando una expresión algebraica tiene un sólo termino algebraico, recibe el nombre de Monomio. Si la expresión algebraica tiene dos términos algebraicos recibe el nombre de Binomio. Si tiene tres términos algebraicos, recibe el nombre de Trinomio. Y en caso contrario si tiene más de tres términos algebraicos, se denomina Multinomio.
Además, las expresiones algebraicas con exponentes positivos se llaman polinomios.
Por ejemplo:
![]() es un monomio (polinomio), pues tiene un solo término algebraico (con exponentes positivos).
es un monomio (polinomio), pues tiene un solo término algebraico (con exponentes positivos).
USO DE PARÉNTESIS
En álgebra, al igual que en aritmética, los paréntesis nos sirven para indicar que las operaciones que ellos encierran tienen prioridad ante las demás, o bien para indicar lo que está dentro de ellos debe ser considerado como un todo.
Para suprimir los paréntesis en una expresión algebraica se siguen las siguientes reglas:
- Si un paréntesis es precedido por un signo positivo, entonces se puede suprimir sin cambiar los signos de los términos que están dentro de ellos.
- En caso contrario, esto es si un paréntesis es precedido por signo negativo, entonces al suprimir el paréntesis los términos que están dentro de él cambian de signo.
- En el caso que a un paréntesis no le preceda ningún signo, entonces se entiende que el paréntesis tiene un signo positivo.
Por ejemplo, en la siguiente expresión, suprimir los paréntesis y reducir los términos semejantes.
![]()
Para resolver este ejercicio se puede hacer de dos formas, una es eliminar inmediatamente los paréntesis y luego reducir los términos semejantes. La segunda forma es reducir los términos semejantes dentro del paréntesis y luego eliminar los paréntesis, y nuevamente reducir términos semejantes. Aplicaremos la segunda forma:
![]()
Polinomios: Un polinomio en es la suma de cualquier numero de monomios.
Definición: Un polinomio en es una suma de la forma:
Donde es un entero no negativo y cada coeficiente de es un numero real. Si es diferente de cero, se dice que el polinomio es de grado.
El coeficiente de la potencia más alta de es el coeficiente principal del polinomio.
1.3. *Planteamiento y resolución de problemas del entorno aplicando propiedades algebraicas
*2. Productos notables y su interpretación geométrica.
Productos notablesProductos notables es el nombre que reciben multiplicaciones con expresiones algebraicas cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.
Factor común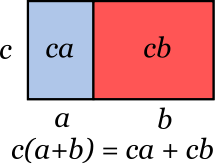
El resultado de multiplicar un binomio a+b por un término c se obtiene aplicando la propiedad distributiva:
![]()
Para esta operación existe una interpretación geométrica, ilustrada en la figura adjunta. El área del rectángulo es
- c(a+b) (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas: ca y cb.
- Ejemplo:
![]()
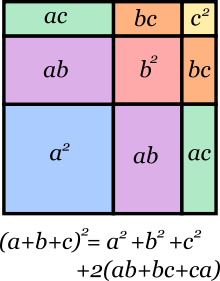
Binomio al cuadrado o cuadrado de un binomio
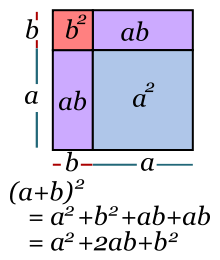
![]()
Un trinomio de la expresión siguiente: ![]() se conoce como trinomio cuadrado perfecto.
se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:
![]()
En ambos casos el signo del tercer término es siempre positivo.
Ejemplo:
![]()
Simplificando:
![]()
Producto de dos binomios con un término común
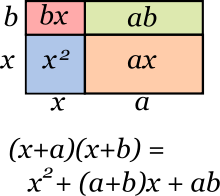
Cuando se multiplican dos binomios que tienen un término común, el cuadrado del término común se suma con el producto del término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.
![]()
Ejemplo:
![]()
Agrupando términos:
![]()
Luego:
![]()
Producto de dos binomios conjugados
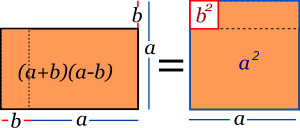
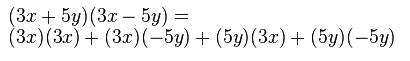
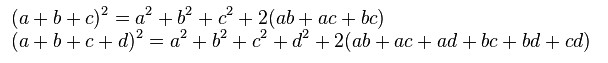
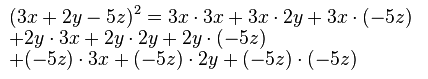
3. Cocientes notables: forma típica, casos su desarrollo y prueba
Son ciertos cocientes que cumplen reglas fijas, evitando así la división de polinomio. También se puede decir, que aquellos que resultan de divisiones exactas entre polinomios, es decir que el resto es igual a cero.Dentro de los diferentes cocientes notables tenemos: la diferencia de los cuadrados de dos cantidades divididas por la suma de estas cantidades, la diferencia de los cuadrados de dos cantidades divididas entre la diferencia de estas cantidades, la suma de los cubos de dos cantidades divididas entre la suma de estas cantidades y la diferencia del cubo de dos cantidades divididas entre la diferencia de estas cantidades.
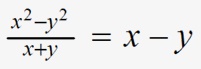
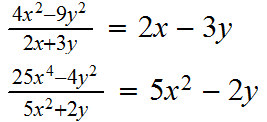
2-) Diferencia de los cuadrados de dos cantidades divididas entre la diferencia de estas cantidades: Es igual a la suma de las dos cantidades en cuestión.
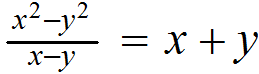
Ejemplos:
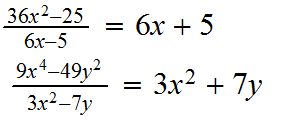
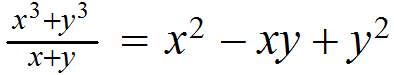
Ejemplos:
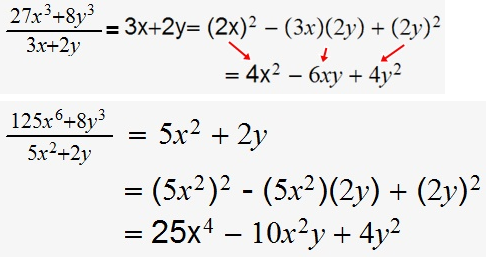
4-) Diferencia del cubo de dos cantidades divididas entre la diferencia de estas cantidades: es igual al cuadrado de la primera cantidad más la multiplicación de la primera cantidad por la segunda cantidad más el cuadrado de la segunda cantidad.
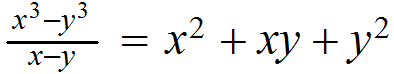
Ejemplos:
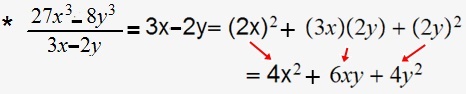
Cocientes Notables
Teoría y Ejercicios de Cocientes Notables
Fuente:https://ue.aprendiendomas.com.bo/pluginfile.php/401/mod_book/chapter/2241/Cocientes-Notables-Ejercicios-Propuestos.pdf
3.1. Formula del término general de un cociente
FORMA GENERAL DE LOS COCIENTES NOTABLES
![]()

4. Teorema del resto
El teorema del resto dice:
Si dividimos un polinomio P(x) entre el binomio (x-a), el resto de la división es igual al valor numérico del polinomio P(a).
¿Para qué nos sirve esto?
Con el teorema del resto podemos calcular el resto de una división sin tener que hacerla, siempre que dividamos un polinomio por un binomio de la forma x-a.
Es decir:
Si queremos saber el resto de la división P(x): Q(x) siendo:
P(x)= 2x2+3x-2
Q(x)= x-2
(2x2+3x-2): (x-2) =
Aplicamos el teorema:
Identificamos en primer lugar “a”, (x-2) en este caso a= 2.
Ahora calculamos el valor numérico del polinomio para a= 2
P(2)= 2.22+3.2-2=12
De este modo observamos como el resto de la división es 12.
Lo comprobamos de la manera tradicional:
Teorema del resto - ejemplo 01
4.1. Teorema del Resto
5. Análisis y estudio del teorema fundamental del álgebra
El Teorema fundamental del álgebra dice que todo polinomio de grado n impar admite o posee al menos una raíz real. Si existe una raíz compleja de un polinomio, entonces existe su raíz compleja conjugada (a-ib).
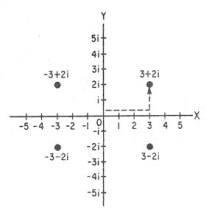
Este teorema resulta de suma importancia dentro del estudio de las ecuaciones. Encontrar la solución de una ecuación representa encontrar todos los valores de x para los cuales la ecuación y(X) = 0 es cierta, a las que comúnmente le llamamos raíces de la ecuación, generalmente las soluciones que de manera inmediata nos interesan son los valores que existan en los reales, sin que con ello las soluciones complejas no sean interesantes. La obtención de soluciones de una ecuación tiene un sentido gráfico que nos es de particular interés. En el caso particular en que las soluciones sean reales estas representan los puntos de intersección con el eje x. Observese la siguiente gráfica: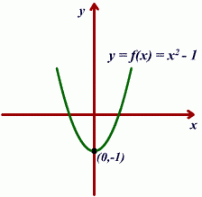
6. Factorización de polinomios y su interpretación geométrica
En matemáticas, la factorización es una técnica que consiste en la descomposición de una expresión matemática (que puede ser un número o una suma). Antes que todo, hay que decir que todo polinomio se puede factorizar utilizando números reales, si se consideran los números complejos. Existen métodos de factorización para algunos casos especiales, que son:
- Diferencia de cuadrados
- Suma o diferencia de cubos.
- Suma o diferencia de potencias impares iguales.
- Trinomio cuadrado perfecto.
- Trinomio de la forma x²+bx+c
- Trinomio de la forma ax²+bx+c.
- Factor común.
- Triángulo de Pascal como guía para factorizar.
Caso I - Factor común DG


Caso II - Factor común por agrupación de términos
Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta dos características, el poli y el nomiotérminos repetidos como variables y números sin factor común, se identifica ya que tiene un número par de términos.
ejemplos :
Factorizar el polinomio ax + ay + 4x + 4y por agrupación de términos.
Observa que los dos primeros términos del polinomio tienen por factor común a.
Los dos últimos términos del polinomio tienen por factor común " 4" y por tanto:
ax + ay + 4x + 4y =(ax + ay)+(4x + 4y)
Agrupando términos. = a(x + y) + 4(x + y)
Factorizando cada grupo por factor común. = (x + y)(a + 4)
Factorizando toda la expresión anterior por factor común.
Caso III - Trinomio cuadrado perfecto
Si se identifica por tener tres términos, de los cuales dos tienen raíces cuadradas exactas, y el restante equivale al doble producto de las raíces del primero por el segundo. Para solucionar un trinomio cuadrado perfecto debemos reordenar los términos dejando el primero y de tercero los términos que tengan raíz cuadrada, o también podemos organizarlos ascendente o descendente (tanto el primero como el tercer termino deben ser positivos); luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término; al cerrar el paréntesis elevamos todo el binomio al cuadrado.
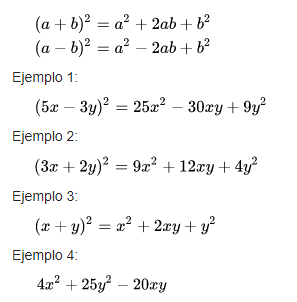
Caso IV - Diferencia de cuadrados perfectos
Se identifica por tener dos términos elevados al cuadrado, unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma (a-b),(a+b), uno negativo y otro positivo).
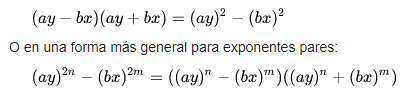
Caso V - Trinomio cuadrado perfecto por adición y sustracción
Se identifica por tener tres términos, dos de ellos son cuadrados perfectos, pero el restante hay que completarlo mediante una suma para que sea el doble producto de las dos raíces (es decir, para completar el Trinomio Cuadrado Perfecto T.C.P.), el valor que se suma es el mismo que se resta para que el ejercicio original no cambie.
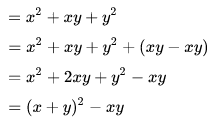
Nótese que los paréntesis en "(xy-xy)" están a modo de aclaración visual.
Caso VI - Trinomio de la forma x2 + bx + c o trinomio simple perfecto
Se identifica por tener tres términos, hay un literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.
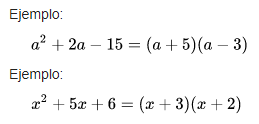
Caso VII - Trinomio de las formas ax2 + bx + c o trinomio compuesto
En este caso se tienen 3 términos: el primer término tiene un coeficiente distinto de uno, la letra del segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, o sea, sin una parte literal, así:
Para factorizar una expresión de esta forma, se multiplica la expresión por el coeficiente del primer término
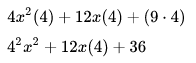
Luego debemos encontrar dos números que multiplicados entre sí den como resultado el término independiente y que su suma sea igual al coeficiente del término x :

Después procedemos a colocar de forma completa el término x2 sin ser elevado al cuadrado en paréntesis, además colocamos los 2 términos descubiertos anteriormente :
Para terminar dividimos estos términos por el coeficiente del término x2 :
Queda así terminada la factorización :
Caso VIII - Suma o diferencia de potencias impares iguales
La suma de dos números a la potencia n, an +bn se descompone en dos factores (siempre que n sea un número impar):
Quedando de la siguiente manera:
Ejemplo:
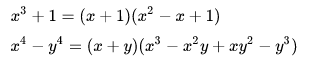
La diferencia también es factorizable y en este caso no importa si n es par o impar. Quedando de la siguiente manera: Ejemplo:
Las diferencias, ya sea de cuadrados o de cubos salen de un caso particular de esta generalización.
Caso IX - Suma o diferencia de cubos perfectos
Su proceso consiste en los siguientes pasos: Suma o diferencia de cubos: a³ ± b³
Suma de cubos
a³ + b³ = (a + b) (a² - ab + b²)
Se resuelve de la siguiente manera
El binomio de la suma de las raíces cúbicas de ambos términos (a + b)
El cuadrado del primer término, [ a² ]
[ - ] el producto de los 2 términos [ ab ]
[ + ] El cuadrado del segundo término; [ b² ]
Ejemplos:
x6 + y6
Se reescribe la ecuación, de tal manera que se pueda factorizar utilizando la suma de cubos.
(x3)2 + (y3)2
De esta manera se podra realizar utilizando la suma de cubos, estableciendo ahora que a = x2 y b = y2
(x2 + y2) ((x2)2 - x2y2 + ((y2)2)
(x2 + y2) (x4 - x2y2 + y4)
Diferencia de cubos
a³ - b³ = (a - b) (a² + ab + b²)
Se resuelve de la siguiente manera
El binomio de la resta de las raíces cubicas de ambos términos (a - b)
El cuadrado del 1er termino, [ a² ]
[ + ] el producto de los 2 términos [ ab ]
[ + ] el cuadrado del 2º término; [ b² ]
Caso X: Posibles ceros
En este primer paso los posibles ceros es el cociente de la división de los divisores del término independiente del polinomio que no está acompañado de una variable entre los divisores del coeficiente principal y se dividen uno por uno.
Nota: Para un mejor entendimiento, este método se explica con el siguiente ejemplo.
Si el enunciado es este:
Se ve que el término independiente es 6 y el coeficiente principal es 1. Para sacar los posibles ceros se procede de la siguiente manera:
Donde se puede notar que como se menciono anteriormente cada divisor de arriba fue dividido por el de abajo; es decir, que el uno se dividió entre uno; el dos se dividió entre uno; el tres se dividió entre uno y por último el seis se dividió entre uno
FACTORIZACIÓN ALGEBRAICA DE POLINOMIOS
Fuente: https://ue.aprendiendomas.com.bo/pluginfile.php/401/mod_book/chapter/2235/factorpol.pdf
6.1. Casos de Factorizacion