LA FORMA EN LA TECNOLOGÍA PROPIA Y APROPIADA
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Matemáticas |
| Libro: | LA FORMA EN LA TECNOLOGÍA PROPIA Y APROPIADA |
| Impreso por: | Invitado |
| Fecha: | jueves, 30 de enero de 2025, 23:24 |
1. Geometría de nuestros pueblos y la geometría euclidiana:
Geometría Euclidiana
La geometría euclidiana corresponde al estudio de las propiedades de los espacios geométricos donde se satisfacen los axiomas de Euclides. Si bien este término a veces es usado para abarcar geometrías que tienen dimensiones superiores con propiedades parecidas, por lo general es sinónimo de geometría clásica o de geometría plana.
En el siglo III a. C. Euclides y sus discípulos escribieron los Elementos, una obra que englobaba el saber matemático de la época dotada de una estructura lógica-deductiva. Desde entonces la geometría se volvió una ciencia, inicialmente para resolver problemas clásicos y evolucionó hasta ser una ciencia formativa que ayuda a razonar.
Historia
Para hablar de la historia de la geometría euclidiana es imprescindible comenzar con Euclides de Alejandría y los Elementos.
Al quedar Egipto en manos de Ptolomeo I, después de la muerte de Alejandro Magno, este comenzó su proyecto en una escuela de Alejandría.
Entre los sabios que enseñaban en la escuela se encontraba Euclides. Se especula que su nacimiento data aproximadamente del 325 a. C. y su muerte del 265 a. C. Podemos saber con certeza que fue a la escuela de Platón.
Durante más de treinta años Euclides enseñó en Alejandría, construyendo sus famosos elementos: comenzó a escribir una descripción exhaustiva de las matemáticas de su tiempo. Las enseñanzas de Euclides produjeron excelentes discípulos, como Arquímedes y Apolonio de Perga.
Euclides se encargó de estructurar los descubrimientos dispares de los griegos clásicos en los Elementos, pero a diferencia de sus predecesores no se limita a afirmar que un teorema es verdadero; Euclides ofrece una demostración.
Los Elementos son un compendio de trece libros. Después de la Biblia, es el libro más editado, con más de mil ediciones.
Los Elementos es la obra maestra de Euclides en el campo de la geometría, y ofrece un tratamiento definitivo de la geometría de dos dimensiones (el plano) y tres dimensiones (el espacio), siendo este el origen de lo que ahora conocemos como geometría euclidiana.
Conceptos básicos
Los elementos están conformados por definiciones, nociones comunes y postulados (o axiomas) seguidos de teoremas, construcciones y demostraciones.
– Un punto es aquello que no tiene partes.
– Una línea es una longitud que no tiene anchura.
– Una línea recta es la que yace por igual con relación a los puntos que están en esta.
– Si dos rectas se cortan de forma que los ángulos adyacentes sean iguales, los ángulos se denominan rectos y las líneas se denominan perpendiculares.
– Rectas paralelas son aquellas que, estando en un mismo plano, nunca se cortan.
Luego de estas y otras definiciones, Euclides nos presenta una lista de cinco postulados y cinco nociones.
Nociones comunes
– Dos cosas que son iguales a una tercera, son iguales entre sí.
– Si a cosas iguales se añaden cosas iguales, los resultados son iguales.
– Si a cosas iguales se le restan cosas iguales, los resultados son iguales.
– Las cosas que coinciden entre sí son iguales entre sí.
– El total es mayor que una parte.
Postulados o axiomas
– Por dos puntos distintos pasa una y solo una recta.
– Las líneas rectas pueden extenderse indefinidamente.
– Se puede dibujar un círculo con cualquier centro y cualquier radio.
– Todos los ángulos rectos son iguales.
– Si una línea recta cruza a dos líneas rectas de modo que los ángulos internos de un mismo lado suman menos que dos ángulos rectos, entonces las dos rectas se cruzarán en ese lado.
Este último postulado se conoce como el postulado de las paralelas y fue reformulado de la siguiente manera: “Por un punto exterior a una recta, se puede trazar una única paralela a la recta dada”.
Ejemplos
A continuación, algunos teoremas de los Elementos servirán para mostrar propiedades de espacios geométricos donde se cumplen los cinco postulados de Euclides; además, ilustrarán los razonamientos lógicos-deductivos de los que se valió este matemático.
Primer ejemplo
Proposición 1.4. (LAL)
Si dos triángulos tienen dos lados y el ángulo entre estos iguales, entonces los otros lados y los otros ángulos son iguales.
Demostración
Sean ABC y A’B’C’ dos triángulos con AB=A’B’, AC=A’C’ y los ángulos BAC y B’A’C’ iguales. Desplacemos al triangulo A’B’C’ de modo que A’B’ coincida con AB y que el ángulo B’A’C’ coincida con el ángulo BAC.
Entonces, la línea A’C’ coincide con la línea AC, de modo que C’ coincide con C. Luego, por el postulado 1, la línea BC debe coincidir con la línea B’C’. Por lo tanto los dos triángulos coinciden y, en consecuencia, sus ángulos y sus lados son iguales.
Segundo ejemplo
Proposición 1.5. (Pons Asinorum)
Si un triángulo tiene dos lados iguales, entonces los ángulos opuestos a esos lados son iguales.
Demostración
Supongamos que el triángulo ABC tiene lados AB y AC iguales.
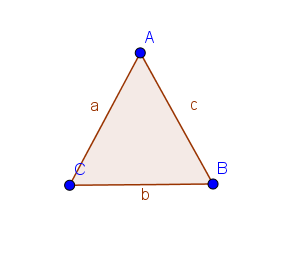
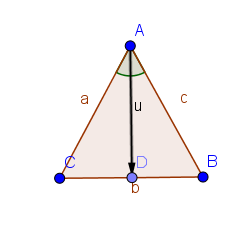
Entonces, los triángulos ABD y ACD tienen dos lados iguales y los ángulos entre estos son iguales. Así, por la proposición 1.4, los ángulos ABD y ACD son iguales.
Tercer ejemplo
Proposición 1.31
Se puede construir una recta paralela a una recta dada por un punto dado.
Construcción
Dada una recta L y un punto P, se traza una recta M que pase por P y corte a L. Luego se traza por P una recta N que corte a L. Ahora, se traza por P una recta N que corte a M, formando un ángulo igual al que L forma con M.
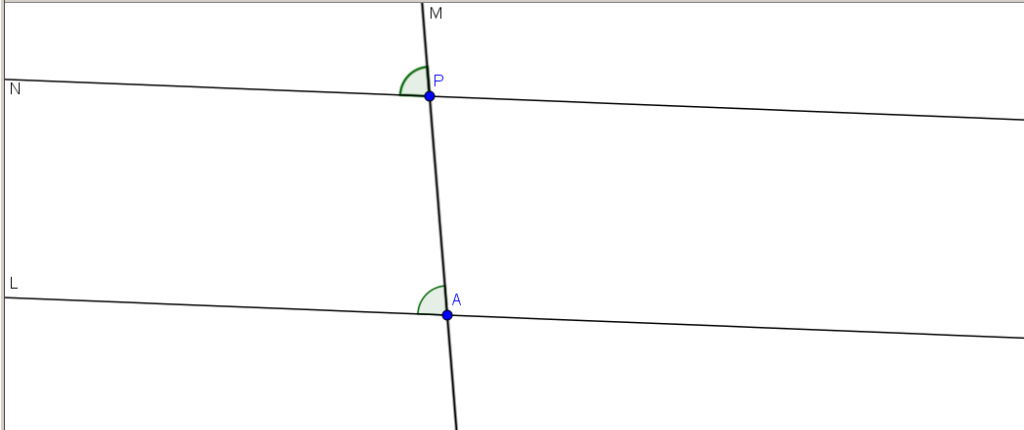
Afirmación
N es paralela a L.
Demostración
Supongamos que L y N no son paralelas y se cortan en un punto A. Sea B un punto en L más allá de A. Consideremos la recta O que pasa por B y P. Entonces, O corta a M formando ángulos que suman menos que dos rectos.
Luego, por 1.5 la recta O debe cortar a la recta L del otro lado de M, así que L y O se cruzan en dos puntos, lo que contradice al postulado 1. Por lo tanto, L y N deben ser paralelas.
Geometría Euclidiana
Fuente: https://ue.aprendiendomas.com.bo/pluginfile.php/400/mod_book/chapter/2224/geometria%20euclidiana.pdf
1.1. Qué es la Geometría Plana o Euclidiana
1.2. Demostración de las propiedades fundamentales de las formas (líneas, triángulos, circunferencias, círculos, etc.).
LAS DEMOSTRACIONES GEOMETRICAS
2. Congruencia y semejanza de figuras planas
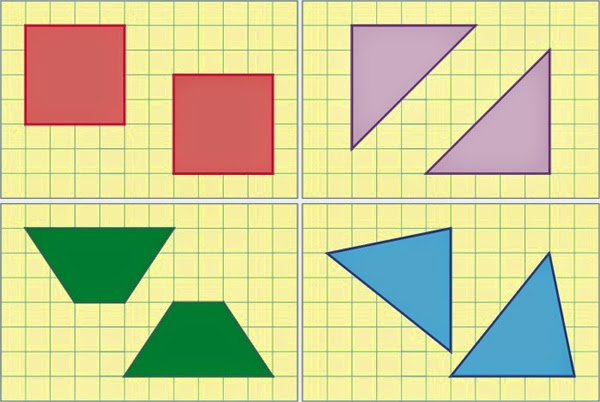
- Todos sus ángulos interiores correspondientes sean iguales.
- Todos sus lados correspondientes tengan la misma medida.
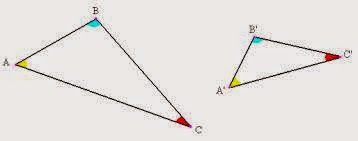
- Sus ángulos correspondientes (homólogos) son iguales.
- Sus lados correspondientes son proporcionales.
2.1. Criterios de congruencia y semejanza
- NO. 1. CRITERIO LLL (LADO,LADO,LADO) Los lados correspondientes son iguales. (Congruentes).
- No. 2.- CRITERIO LAL (Lado,ángulo, lado). Los 2 lados correspondientes y elángulo que forman son iguales.
- No. 3.- CRITERIO ALA (Ángulo, lado, ángulo). Dos ángulos correspondientes y el lado común son iguales.

Para que dos triángulos sean semejantes basta que se cumpla cualquiera de los siguientes criterios:
Sus
- No. 1.-CRITERIO LLL (Lado,lado,lado). Sus lados correspondientes sonproporcionales.
- No. 2.- CRITERIO LAL (Lado,ángulo, lado). Un ángulo correspondiente es igual y los lados que lo forman son proporcionales.
- No. 3.- CRITERIO AA (Ángulo, ángulo). Dos ángulos correspondientes soniguales. (Recuerda que la suma de ángulos interiores de un triángulo suman 180 grados, por lo tanto conociendo dos lados, podemos obtener la medida del tercer ángulo faltante).
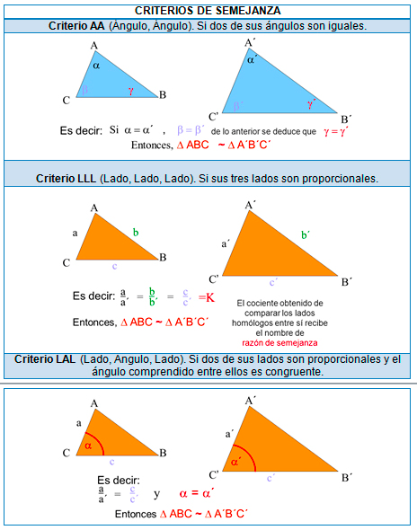
2.2. Interpolación de triángulos semejantes para determinar la medida de un lado.
Métodos de interpolaciónFuente: https://ue.aprendiendomas.com.bo/pluginfile.php/400/mod_book/chapter/2229/metodos%20de%20interpolacion.pdf
3. Razón y proporción entre segmentos.
La razón de dos segmentos AB y CD es la medida del primero respecto del segundo que estaríamos tomando como unidad.
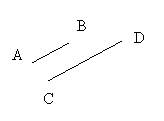
En esta figura la razón entre los segmentos AB y CD sería 1/2. Esta relación se expresa así:
![]()
Si calculamos la razón de dos segmentos, conociendo la medida de cada uno de ellos con respecto a un segmento unidad, el resultado es siempre el mismo independiente de la unidad de medida elegida , aunque ha de ser siempre la misma para medir ambos segmentos.
4. El teorema de Tales
Teorema de Tales
Éste es el teorema básico de las semejanzas.
El Teorema de Tales dice: Si dos rectas, no necesariamente paralelas, son cortadas por un sistema de rectas paralelas, entonces los segmentos que resultan sobre una de las dos rectas son proporcionales a los correspondientes segmentos obtenidos sobre la otra.
A continuación, damos una figura para ejemplificar el enunciado anterior:
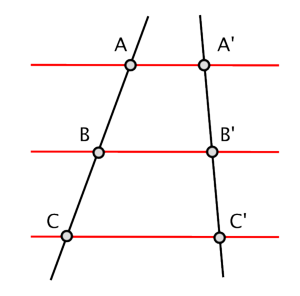
dónde se cumple que 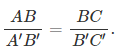
Ejemplo
Por ejemplo, dada la figura siguiente, decidir si son o no semejantes los segmentos resultantes.
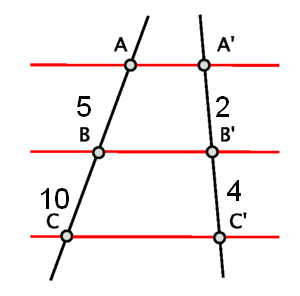
Como observamos en la figura, las longitudes de los segmentos son los siguientes: ![]() Por el Teorema de Tales, se ve que los segmentos de una recta y otra son semejantes gracias a que las razones son iguales:
Por el Teorema de Tales, se ve que los segmentos de una recta y otra son semejantes gracias a que las razones son iguales:
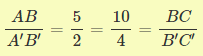
Para terminar, vamos a dar una aplicación que puede resultar muy útil para la resolución de determinados ejercicios. Gracias al Teorema de Tales, podemos calcular la altura de un objeto, por ejemplo, un árbol, mediante el siguiente mecanismo.
- Sea C
- Sea B
- Sea A
Entonces, se cumple que la altura del árbol, llamada H, se obtiene mediante la siguiente igualdad:
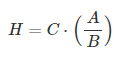
4.1. Teorema de Tales | Introducción
4.2. Teorema de Tales
5. Fractales y su relación con la naturaleza.
Una hoja de helecho, un copo de nieve, un pulmón o un riñón humano; una nube, la costa de Inglaterra… ¿qué tienen en común? “Fueron hechos perfectos y bellos por el creador de todas las cosas”, diría posiblemente un escolástico medieval. Un matemático moderno dice: “Son fractales”.
Los fractales son estructuras geométricas que tienen la propiedad de repetir un mismo elemento geométrico o espacial en cada plano, una y otra vez. Un buen ejemplo de ello, en la naturaleza, es el helecho, cuyas hojas producen copias cada vez más pequeñas de si mismas. Otro ejemplo de fractal lo presentó Apolonio de Perge -discípulo de Euclides, aprox. en el 200 a.C.- creando una figura compuesta de esferas cada vez más pequeñas (imagen arriba).
Los fractales despiertan hoy un interés de carácter variadísimo. Se da entre artistas, periodistas, músicos y científicos. ¿Por qué? Desde luego, no porque los fractales posean -como de hecho es- tanta belleza y aún cuando su estética sea realmente innegable. Y desde luego, tampoco porque los fractales se cuenten entre los conceptos más modernos de la matemática, que tienen aplicación en muchos campos de la vida diaria y la tecnología. Más bien pensamos que los fractales atraen a todos porque reflejan arquetipos universales que se expresan en todos los niveles de la creación. Se los encuentra en la naturaleza, en la evolución del cosmos y en los diferentes campos de la sociedad. En estas estructuras omnipresentes, el hombre también puede reconocerse a sí mismo y ver reflejado su propio camino. Quiera este viaje por el mundo de los fractales hacernos avanzar un paso más en el camino del conocimiento.
Comenzaremos por una explicación matemática que, en caso de una lectura rápida, se podría obviar. Luego seguiremos con la descripción de diferentes facetas de los fractales en la naturaleza, el arte, la música, la literatura y la ciencia, que demuestran la presencia universal de estas estructuras arquetípicas. Finalmente, cerraremos con deducciones filosóficas referentes a las reflexiones fractales en el hombre mismo y lo que se puede aprender de ellas.

2. Aspectos matemáticos de los fractales
Fractales son el concepto general para una clase bastante amplia de objetos geométricos (conjuntos) que tienen la propiedad de ser autosemejantes. Autosemejante significa que, estas estructuras, se componen de copias cada vez más pequeñas de sí mismas. El ejemplo más conocido es la llamada “alfombra de Sierpinski”, que se compone de una copia óctuple de si misma, en factor 3 de reducción. La análoga, en tres dimensiones, es la esponja de Menger, llamada así según el matemático Karl Menger (1902-1985).

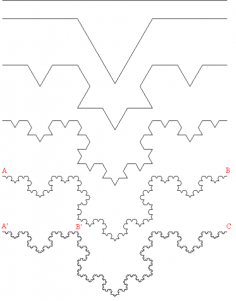
Un conjunto autosemejante también muy conocido es la curva de Koch, con cuya ayuda se puede crear un maravilloso copo de nieve. Este copo de nieve es un fractal, pero no autosemejante en sentido estricto, porque no se compone de copias de si mismo, sino que sólo los bordes se reproducen a sí mismos.
Muchos fractales autosemejantes se construyen “borrando” ciertas partes de un conjunto base (en el caso de la alfombra de Sierpinski, un cuadrado) dentro de una cantidad infinita de repeticiones. Se van borrando partes cada vez más pequeñas, formándose una estructura fractal.
Una construcción alternativa (que lleva el nombre del matemático australiano Michael Barnlsey) se forma reduciendo el tamaño del conjunto base, y luego copiándolo y ordenándolo correctamente (por medio de giros y desplazamientos), repitiendo el proceso infinitamente. Así se forma, por ejemplo, el famoso fractal de la hoja de helecho (primera ilustración).
Un patrón de medida para el “tamaño” de un conjunto fractal y su distribución uniforme es la dimensión autosemejante, que se define como la relación entre el logaritmo natural (ln) de la cantidad de copias del conjunto, en cada paso de la construcción, y el logaritmo del factor de reducción. Así, por ejemplo, la dimensión autosemejante de la alfombra de Sierpinski (8 copias de si misma por paso de construcción, factor de reducción 3) es igual a ln 8 : ln 3 = 1,8927. Este concepto conceptualiza la bien conocida dimensión del espacio. De esta manera, la dimensión de muchos fractales reproducibles en un plano se sitúa entre 1 (dimensión de la línea recta) y 2 (dimensión de un plano).
La palabra fractal fue propuesta en el año 1975 por el padre de la geometría fractal, el matemático polaco de adopción francesa Benoit Mandelbrot. Significa “quebrado, fraccionado, roto” y se refiere, entre otras cosas, a aquella dimensión que a menudo es claramente un número no-entero.
A través de las relaciones numéricas que se dan en los logaritmos (en el caso anterior sería 8:3) los fractales autosemejantes se pueden relacionar con la doctrina de los números y proporciones pitagóricas y, por lo tanto, con la partición de la cuerda (del monocordio), con la doctrina de la armonía musical y de los movimientos de los planetas. Nos podríamos preguntar por ejemplo, qué fractales surgen a través de relaciones numéricas “armónicas” 1:2, 2:3, 3:4, etc. o sea de una relación (musical) de cuarta. De la misma manera, las relaciones de los semiejes de órbitas planetarias en el sistema solar corresponden a proporciones armónicas (doctrina de la armonía cósmica de Johannes Kepler). Con la misma combinación numérica, se puede asociar a fractales la mística pitagórica de los números. Así por ejemplo, el número 3 se puede asignar a la Tríada espiritual, el 4 a la materia y el número 5 al hombre (microcosmos), y con ello llegar a los correspondientes significados para los conjuntos fractales. Simbólicamente, la curva de Koch (y por lo mismo el copo de nieve) podría representar una relación entre los números 3 y 4, o sea entre espíritu y materia, cielo y tierra.
Otra clase importante de fractales son los fractales aleatorios, como por ej. las líneas de un movimiento browniano que representen el movimiento termodinámico caótico de una pequeña partícula en el agua. Tales fractales son conjuntos aleatorios que sólo son “autosemejantes” en un sentido muy irregular. Esto significa que las leyes de la casualidad que los rigen son independientes de la escala y no cambian cuando “aumentamos con el zoom” el conjunto.
3. Autosemejanza en la naturaleza
Los fractales, sean de origen natural o creados matemáticamente, ofrecen un alto grado de autosemejanza. Autosemejanza significa aquí que se repiten formaciones a diferentes niveles de tamaño. Este es el caso por ejemplo, de cuando un objeto se compone de copias reducidas de si mismo (ver por ej. la esponja de Menger o la curva de Koch del punto anterior). Esta propiedad reproduce hasta el infinito en los fractales ideales construidos por cálculo matemático. Al contrario de las formas geométricas, que cuanto más se aumenta la visión más planas y por lo mismo más sencillas aparecen (por ej. una circunferencia), en los fractales aparecen cada vez más detalles y más complejos.

La autosemejanza en este caso no tiene por qué ser perfecta. En los fractales naturales, la cantidad de niveles autosemejantes de estructuras es limitada y a menudo se sitúa entre 3-5. Ejemplos de esto pueden ser árboles, plantas, nubes, líneas costeras, rocas, arena, copos de nieve e incluso nuestro universo como conjunto, que muestra estructuras fractales de súper-galaxias. Estas formaciones están estructuradas en menor o mayor medida en algunos niveles. Una rama, por ejemplo, tiene más o menos la apariencia de un pequeño árbol. La propiedad de la autosemejanza lleva también a que –por lo menos a determinados niveles aumento- no se pueda decir qué tamaño tenga una sección que estemos contemplando por ejemplo en una foto. El mismo Benoit Mandelbrot habla de la „geometría fractal de la naturaleza“.
4. Distintas facetas de los fractales
4.1 Arte y arquitectura
Por su dimensión, los fractales están relacionados estrechamente con las proporciones (del arte). Como sabemos, el arquetipo de belleza se expresa entre otras cosas a través de proporciones idóneas. Se pueden encontrar en todos los apartados del arte: en la música con la llamada escala natural (o de tonos concomitantes) y sus intervalos armónicos como la quinta o la cuarta; en monumentos egipcios, estatuas griegas o jardines Zen, todos ellos basados en el número áurico u otras proporciones, por mencionar sólo unos ejemplos.
Los fractales, descubiertos y propuestos por Mandelbrot durante el siglo XX son uno de los grandes hallazgos matemáticos recientes. Aunque dar una definición exacta de qué es un fractal es complejo, tienen dos características clave: son autosimilares y siguen un algoritmo recursivo.
Que sean autosimilares quiere decir que su forma es hecha a partir de copias más pequeñas de la misma figura. Hasta el infinito. Se relacionan por tanto estrechamente con el número de Fibonacci y están presentes por todas partes en la naturaleza, desde la rama de un árbol a como cae el agua en las cascadas. Aquí tienes 10 maravillosos ejemplos de como la naturaleza es, en el fondo, pura matemática.
Romanescu

Copos de nieve

Helechos

Grietas por la sequía

Las plumas de un pavo real

Rayos

Una hoja

5.1. Fractales en la naturaleza