MEDIDA DE LAS FORMAS Y LA REPRESENTACIÓN GRÁFICA DE LOS PROCESOS DE PRODUCCIÓN
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 2° - Matemáticas |
| Libro: | MEDIDA DE LAS FORMAS Y LA REPRESENTACIÓN GRÁFICA DE LOS PROCESOS DE PRODUCCIÓN |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 08:46 |
Tabla de Contenidos
- 1. Instrumentos de medición: flexómetro, escuadra, transportador, distanciómetro, eclímetro etc.
- 2. Ángulos: Sistemas de medidas de ángulos
- 2.1. Ángulos (Biblioteca de KUAA)
- 2.2. Sistema Radial
- 2.3. Qué es un Radián
- 2.4. Sistema sexagesimal
- 2.5. Expresión de ángulos en el sistema sexagesimal
- 2.6. Sistema centesimal
- 2.7. Sistema centesimal video explicado
- 2.8. Métodos de conversión entre los sistemas de medida de ángulo
- 2.9. Convertir grados a radianes y viceversa
- 2.10. Conversiones de radianes a grados y de grados a radianes
- 3. Clasificación de los ángulos
- 4. Relaciones entre Ángulos
- 5. Ángulos entre rectas paralelas cortadas por una secante
- 6. Elementos de la Circunferencia y del círculo.
- 7. Líneas notables, arco, perímetro y área aplicadas a actividades técnicas y tecnológicas del nuestro entorno
- 8. NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (BIBLIOTECA KUAA)
1. Instrumentos de medición: flexómetro, escuadra, transportador, distanciómetro, eclímetro etc.
Cinta Métrica
Una cinta métrica o un flexómetro es un instrumento de medida que consiste en una cinta flexible graduada y se puede enrollar, haciendo que el transporte sea más fácil. También se pueden medir líneas y superficies curvas.

Transportador
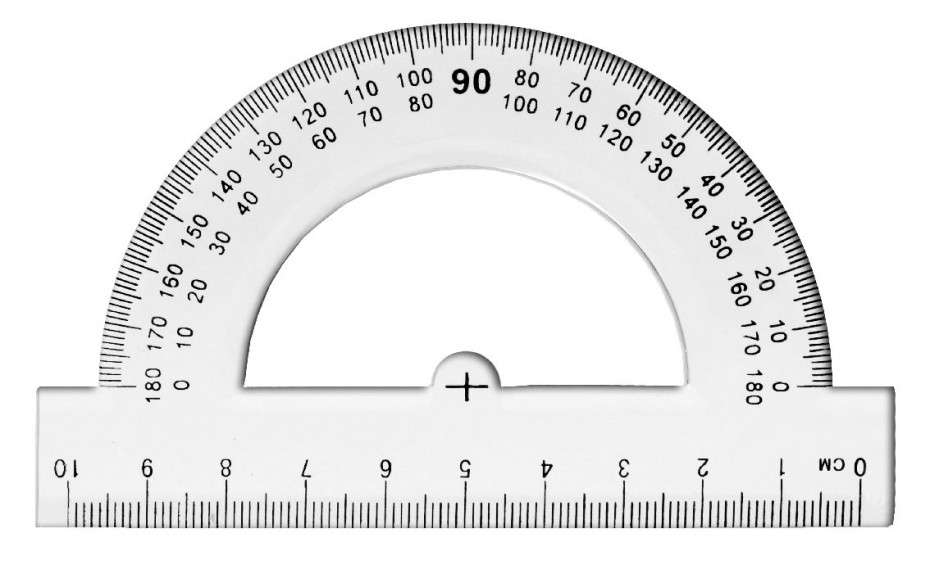
•Un transportador es un instrumento de medición de ángulos en grados que viene en dos presentaciones básicas:
•Transportador con forma semicircular graduado en 180° (grados sexagesimales) o 200g (grados centesimales). Es más común que el circular, pero tiene la limitación de que al medir ángulos cóncavos (de más de 180° y menos de 360°), se tiene que realizar una doble medición.
•Transportador con forma circular graduado en 360°, o 400g.
Escuadra
•La escuadra de comprobación es una herramienta para el trabajo en carpintería o metalistería, usada para marcar y medir una pieza de material.
•Consta de una paleta ancha, fabricada de acero o bronce y remachada a un mango de madera. El interior del mango se encuentra generalmente fijado con un listón metálico, para asegurar que la paleta quede inmóvil debidamente a 90 grados.

Distanciómetro

El Eclímetro
El eclímetro es un instrumento topográfico, está formado por un tubo alargado de sección cuadrada (en nuestro caso era metálico), también posee un trasportador el cual se encuentra atornillado al tubo.
Cuenta con un brazo indicador, el cual nos señalará la magnitud del ángulo. Posee un hilo metálico, el cual haremos coincidir con algún objeto para poder medir los ángulos.
El eclímetro lleva un nivel de aire, y en uno de los extremos posee un visor, debemos resaltar que este visor no tiene ningún dispositivo de aumento, por este visor observaremos el hilo metálico y la burbuja de aire del nivel, podemos observar dicha burbuja gracias a que el eclímetro posee una ventanilla con un espejo, es por este espejo por el cual podremos observar el nivel de aire. Compás Tubo cuadrado Brazo indicador.

2. Ángulos: Sistemas de medidas de ángulos
En la medida de ángulos, y por tanto en trigonometría, se emplean cuatro unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.
Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes.
Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
Horario: su unidad de medida es el ángulo de 1 hora, que equivale a la sexta parte del ángulo recto.
2.1. Ángulos (Biblioteca de KUAA)
NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (LIBRO PROPORCIONADO POR LA BIBLIOTECA DE KUAA)
ESCUELA DE MATEMÁTICAS UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN
Ángulos
En esta lección presentaremos muy brevemente los conceptos básicos de la geometría necesarios para la mejor comprensión del curso. También iniciaremos el estudio de la trigonometría a partir del teorema de Pitágoras y definiremos las relaciones trigonométri- cas de los ángulos agudos de un triángulo rectángulo y sus relaciones recíprocas.
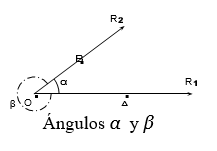
Ángulo es la abertura formada por dos rayos (o semirrectas) que tienen un origen común, llamado vértice del ángulo . Cada uno de los rayos R1 y R2 se denomina lado del ángulo. Se utilizan varias notaciones para los ángulos. Las más comunes son:
- ∠AOB, en términos de las semirrectas OA y OB. También puede utilizarse ∠BOA.
- Con frecuencia se utiliza una única letra, la cual puede ser una letra minúscula a, b, c, . . . o también una letra griega como α (alfa), β (beta), γ (gamma), δ (delta), ϕ (fi),. . . , para representar el ángulo y para representar su medida.
- También se utilizará el vértice O para denotar el ángulo.
Dos rayos R1 y R2 que tienen un origen común O dan lugar a dos ángulos (α y β) como se puede ver en la figura. El ángulo queda plenamente identificado a partir de condiciones adicionales.
Medida de ángulos
Medir un ángulo es compararlo con otro que se toma como unidad. Utilizaremos dos unidades de medida: el grado sexagesimal y el radián.
Sistema sexagesimal
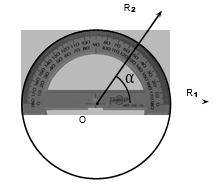
Consideramos una circunferencia de centro O dividida en 360 partes iguales. Si unimos cada una de estas 360 divisiones con el centro O, se forman 360 ángulos. Un ángulo mide un grado, escrito 1◦, si tiene su vértice en el centro O y sus lados cortan dos divisiones sucesivas de la circunferencia. De acuerdo con esta definición el ángulo que corresponde a una rotación completa alrededor del vértice O mide 360◦.
Para medir ángulos se utiliza el transportador. En el transportador, que se presenta en la figura se aprecian las 180 divisiones de una semicircunferencia. el ángulo α que forman los rayos R1 y R2 es un ángulo de 55◦.
Sistema circular
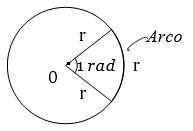
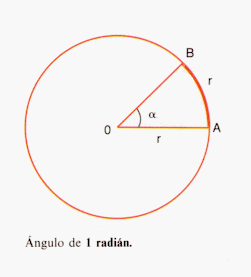
En este sistema para medir ángulos, se utiliza como unidad de medida el radián, denotado 1 rad. Consideremos una circunferencia con centro en el punto O y radio r. Un radián es un ángulo con vértice en O y cuyos lados son dos radios de la circunferencia que determinan un arco cuya longitud es igual al radio r de la circunferencia.
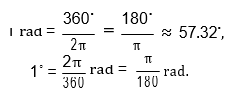
2.2. Sistema Radial
Este sistema tiene como unidad de medida el RADIÁN, que es el ángulo que encierra entre sus lados un arco de circunferencia con centro en su vértice, de longitud igual al radio de la misma.
Teniendo en cuenta que la longitud de la circunferencia es:
![]()
La medida de una circunferencia en radianes es:
2.3. Qué es un Radián
2.4. Sistema sexagesimal
El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo.
La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.
A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).
• Medidas de ángulos: 1 grado (º) → 60 minutos (´) → 60 segundos (´´)
• Medidas de tiempo: 1 hora → 60 minutos (´) → 60 segundos (´´)
Por tanto, en general, un ángulo en el sistema sexagesimal vendrá expresado en grados, minutos y segundos, de la forma, por ejemplo: 38º 50´ 35´´ (38 grados, 50 minutos y 35 segundos). Si se omiten los minutos y segundos, por ejemplo, 45º, es porque se entiende que es 45º 0´ 0´´.
Cuando un ángulo se mide en grados, minutos y segundos, se dice que está expresado con medida compleja, mientras que si se expresa con una sola clase de unidades, se dice que es una medida incompleja o simple, por ejemplo:
32º → medida simple
11´´ → medida simple
52º 17´ 45´´ → medida compleja
4º 22´ → medida compleja
2.5. Expresión de ángulos en el sistema sexagesimal
2.6. Sistema centesimal
El grado centesimal, grado centígrado o gradián (plural: gradianes), originalmente denominado gon, grade o centígrado —nombres aún en uso en otros idiomas, por ejemplo en portugués se escribe grado— resulta de dividir un ángulo recto en cien unidades. La circunferencia se divide, así, en 400 grados centesimales. Un grado centesimal equivale a nueve décimos de grado sexagesimal. En las calculadoras suele usarse la abreviatura grad. Se representa como una "g" minúscula en superíndice colocada tras la cifra. Por ejemplo: 12,4574g- 1 grado centesimal = 100 minutos centesimales (100m o 100c)
- 1 minuto centesimal = 100 segundos centesimales (100s o 100cc)
2.7. Sistema centesimal video explicado
2.8. Métodos de conversión entre los sistemas de medida de ángulo
Métodos de conversión entre los sistemas de medida de ángulo
Pasar de radianes a grados sexagesimales
Para pasar de radianes a grados sexagesimales hay que recordar la relación para un ángulo que describe una circunferencia completa expresado en grados y radianes, como:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados y radianes es la siguiente:
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular los grados sexagesimales a partir de radianes, se despeja G de la expresión anterior, quedando:
| R |
|
G = | · 360º | |
| 2·π |
|
- EJEMPLO 1: Pasar 1 radián a grados sexagesimales
Sustituyendo el valor de 1 radián en la expresión anterior resulta:
| 1 |
|
G = | · 360º = 57,29578º | |
| 2·π |
|
Por tanto, 1 rad = 57,29578º
También se puede expresar la medida de ángulo obtenida en forma compleja (grados minutos y segundos) de la siguiente forma:
Grados: 57,29578º = 57º + 0,29578º
Minutos: 0,29578º → 0,29578 · 60 = 17,7468´ → 17,7468´ = 17´+ 0,7468´
Segundos: 0,7468´ · 60 = 44,81´´
Por tanto, 1 rad = 57,29578º = 57º 17´ 44,81´´ (57 grados 17 minutos 44,81 segundos)
- EJEMPLO 2: Pasar π/4 radianes a grados sexagesimales
Sustituyendo π/4 en la expresión anterior se obtiene:
| π/4 |
|
G = | · 360º = 45º | |
| 2·π |
|
Por tanto, π/4 rad = 45º. O también:
π/4 rad = 45º = 45º 0´ 0´´ (45 grados 0 minutos 0 segundos)
Pasar de radianes a grados centesimales
Para pasar de radianes a grados centesimales se parte de la relación que hay para un ángulo que describe una circunferencia completa expresado en grados centesimales y radianes:
400 g = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados centesimales y radianes es la siguiente:
| C | = | R |
| 400g | 2 · π |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se pide es calcular los grados centesimales a partir de radianes, se despeja C de la expresión anterior, quedando:
| R |
|
C = | · 400 g | |
| 2·π |
|
- EJEMPLO: Pasar 2 radianes a grados centesimales
Sustituyendo el valor de 2 radianes en la expresión anterior resulta:
| 2 |
|
C = | · 400 g = 127,3240 g | |
| 2·π |
|
Por tanto, 2 rad = 127,3240 g
El resultado anterior del ángulo se puede expresar también en forma compleja (grados minutos y segundos) de la siguiente forma:
Grados Centesimales: 127,3240g = 127g + 0,3240g
Minutos: 0,3240g → 0,3240 · 100 = 34,40m → 32,40m = 32m + 0,40m
Segundos: 0,40 · 100 = 40s
Por tanto, 2 rad = 127,3240 g = 127g 32m 40s (127 grados centesimales 32 minutos 40 segundos)
Pasar de grados sexagesimales a radianes
Para pasar de grados sexagesimales a radianes se parte de nuevo de la relación de un ángulo completo expresado en grados sexagesimales y radianes:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y radianes es la ya conocida:
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular el valor en radianes de un ángulo expresado en grados sexagesimales, se despeja R de la expresión anterior, quedando:
| G |
|
R = | · 2 · π | |
| 360º |
|
- EJEMPLO 1: Pasar un ángulo de 45º a radianes
Sustituyendo el valor de 45º en la expresión anterior resulta:
| 45º |
|
R = | · 2 · π = π/4 | |
| 360º |
|
Por tanto, 45º = π/4 radianes.
Pasar de grados sexagesimales a grados centesimales
Para pasar de grados sexagesimales a centesimales se parte de la relación del ángulo que describe una circunferencia completa expresado en grados sexagesimales y centesimales:
1 vuelta completa = 360º = 400 g
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y centesimales sería:
| G | = | C |
| 360º | 400 g |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
C es la medida del ángulo expresada en grados centesimales (g)
Si lo que se pide es calcular los grados centesimales a partir de grados sexagesimales, se despeja C de la expresión anterior, quedando:
| G |
|
C = | · 400 g | |
| 360º |
|
- EJEMPLO 1: Pasar 90º sexagesimales a centesimales
Sustituyendo el valor de 90º en la expresión anterior resulta:
| 90º |
|
C = | · 400 g = 100 g | |
| 360º |
|
Por tanto, 90º = 100 g
- EJEMPLO 2: : Pasar un ángulo expresado en el sistema sexagesimal de 23º 37´ 45´´ a grados centesimales
En primer lugar, habrá que pasar el ángulo expresado en grados minutos y segundos (forma compleja) a simple (sólo en grados). Para pasar 23º 37´ 45´´ a forma simple (º) se opera de la siguiente forma:
1º) Los grados se dejan en grados: 23º → 23º
2º) Los minutos se pasan a grados: 37´ → 37´/60 = 0,6167º
3º) Los segundos se pasan a minutos, y éstos a grados: 45´´ → 45´´/60 = 0,75´ → 0,75´/60 = 0,0125º
4º) Se suman todos los grados obtenidos: 23º + 0,6167º + 0,0125º = 23,6292º
Por tanto, 23º 37´ 45´´ = 23,6292º
Ahora se aplica la expresión anterior para pasar de grados sexagesimales a centesimales:
| 23,6292º |
|
C = | · 400 g = 26,2547 g | |
| 360º |
|
Por tanto, 23,6292º = 26,2547 g
Por último, sólo faltará expresar los grados centesimales obtenidos en forma simple a forma compleja (grados, minutos y segundos centesimales):
Grados Centesimales: 26,2547g = 26g + 0,2547g
Minutos: 0,2547g → 0,2547·100 = 25,47m → 25,47m = 25m+ 0,47m
Segundos: 0,47m·100 = 47s
Por tanto, finalmente se tiene que: 23,6292º = 26,2547g = 26g 25m 47s
Pasar de grados centesimales a grados sexagesimales
Para pasar de grados centesimales a sexagesimales se parte, como en el apartado anterior, de la relación del ángulo que describe una circunferencia completa expresado en grados centesimales y sexagesimales:
1 vuelta completa = 400 g = 360º
Por tanto, de nuevo la expresión general que permite relacionar las medidas de un ángulo expresado en grados centesimales y sexagesimales sería:
| C | = | G |
| 400 g | 360º |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
G es la medida del ángulo expresada en grados sexagesimales (º)
Si lo que se pide es calcular los grados sexagesimales a partir del ángulo expresado en grados centesimales, se despeja G de la expresión anterior, quedando:
| C |
|
G = | · 360º | |
| 400 g |
|
- EJEMPLO 1: Pasar 90 g centesimales a grados sexagesimales
Sustituyendo el valor de 90 g en la expresión anterior resulta:
| 90 g |
|
G = | · 360º = 81º | |
| 400 g |
|
Por tanto, 90 g = 81º
- EJEMPLO 2: : Pasar un ángulo expresado en el sistema centesimal 43g 21m 58s a grados sexagesimales (expresando también el resultado en grados minutos segundos sexagesimales)
En primer lugar, habrá que pasar el ángulo expresado en grados minutos y segundos centesimales (forma compleja) a la forma simple (sólo grados). Para pasar 43g 21m 58s a forma simple (sólo grados) se opera de la siguiente forma:
1º) Los grados centesimales se dejan en grados centesimales: 43g → 43g
2º) Los minutos centesimales se pasan a grados centesimales: 21´ → 21´/100 = 0,21g
3º) Los segundos centesimales se pasan a minutos centesimales, y éstos a grados centesimales: 58´´ → 58´´/100 = 0,58´ → 0,58´/100 = 0,0058g
4º) Se suman todos los grados centesimales obtenidos: 43g + 0,21g + 0,0058g = 43,2158 g
Por tanto, 43g 21m 58s = 43,2158 g
Ahora se aplica la expresión anterior para pasar de grados centesimales a grados sexagesimales:
| 43,2158 g |
|
G = | · 360º = 38,8942º | |
| 400 g |
|
Por último, sólo faltará expresar los grados sexagesimales obtenidos a la forma compleja (grados, minutos y segundos), de la siguiente forma:
Grados: 38,8942º = 38º + 0,8942º
Para obtener los minutos: 0,8942º → 0,8942 · 60 = 53,6520´ → 53,6520´ = 53´+ 0,6520´
Para obtener los segundos: 0,6520´ · 60 = 39,12´´
Por tanto, 43 g 21 m 58 s = 38,8942º = 38º 53´ 39,12´´ (38 grados 53 minutos 39,12 segundos sexagesimales)
2.9. Convertir grados a radianes y viceversa
2.10. Conversiones de radianes a grados y de grados a radianes
3. Clasificación de los ángulos
Clasificación de ángulos según su medida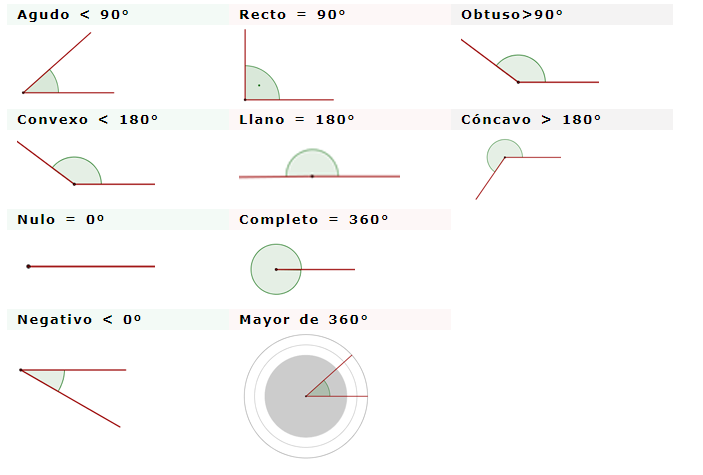
Ángulos consecutivos
Ángulos consecutivos son aquellos que tienen el vértice y un lado común.
Ángulos adyacentes
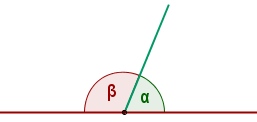
Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.
Forman un ángulo llano.
Ángulos opuestos por el vértice
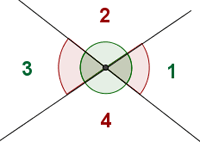
Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.
Los ángulos 1 y 3 son iguales.
Los ángulos 2 y 4 son iguales.
Clasificación de ángulos según su sumaÁngulos complementarios
Dos ángulos son complementarios si suman 90°.
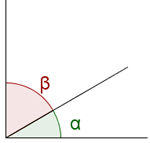
Dos ángulos son suplementarios si suman 180°.
Ángulos resultantes del corte entre dos rectas paralelas y perpendiculares entre sí
Ángulos correspondientes
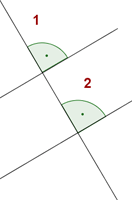
Los ángulos 1 y 2 son iguales.
Ángulos alternos internos
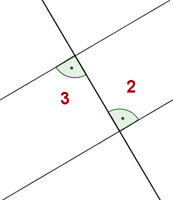
Los ángulos 2 y 3 son iguales.
Ángulos alternos externos
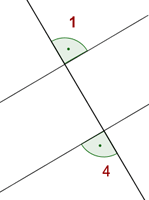
Los ángulos 1 y 4 son iguales.
3.1. Clasiftcación de los ángulos según su medida (Biblioteca de KUAA)
NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (LIBRO PROPORCIONADO POR LA BIBLIOTECA DE KUAA)
ESCUELA DE MATEMÁTICAS UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN
Clasiftcación de los ángulos según su medida• Ángulo nulo. Es el ángulo que mide 0◦.
• Ángulo agudo. Es el ángulo que mide más de 0◦ y menos de 90◦.
• Ángulo recto. Es el ángulo que mide exactamente 90◦.
• Ángulo obtuso. Es el ángulo que mide más de 90◦ y menos de 180◦.
• Ángulo llano. Es el ángulo que mide 180◦.

Relaciones entre ángulos
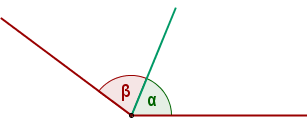
- Ángulos congruentes: decimos que dos ángulos son congruentes si tienen la misma medida. Si los ángulos α y β son congruentes escribimos α ∼= β.
- Ángulos complementarios: dos ángulos son complementarios si la suma de sus medidas es 90◦.
- Ángulos suplementarios: dos ángulos son suplementarios si la suma de sus medidas es 180◦.
Si dos ángulos α y β son complementarios, decimos que α es el ángulo complementario de β. Similarmente si dos ángulos α y β son suplementarios decimos que α es el ángulo suplementario de β.
Ejemplo
Los ángulos a y b que aparecen en la figura son congruentes; los ángulos c y d son complementarios y los ángulos e y f son suplementarios.
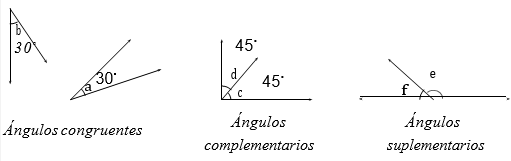
Notación. Con el propósito de simplificar la escritura utilizaremos la misma notación para representar tanto el ángulo como su medida. El texto completo nos va a permitir interpretar correctamente en que sentido se utilizan los símbolos. Por ejemplo escribimos a = b para significar que la medida del ángulo a es igual a la medida del ángulo b. También podremos escribir a + b = 180◦, para indicar que la suma de las medidas de los ángulos a y b en grados es 180◦. La afirmación c + d = \pi / 2 rad, indica que la suma de las medidas de los ángulos c y d en radianes es \pi / 2 radianes

3.2. Clasificación de ángulos
4. Relaciones entre Ángulos
- Ángulos complementarios: Son los que suma 90º.
- Ángulos suplementarios: Son los que suman 180º.
- Ángulos consecutivos o contigüos: Tienen un lado común.
- Ángulos adyacentes: Ángulos que tienen una lado en común y el otro lado sobre una misma recta. Tiene la propiedad de ser suplementarios.
- Ángulos opuestos por el vértice: Dos ángulos son opuestos por el vértice, cuando al prolongar los lados de un ángulo se forman los lados del otro ángulo
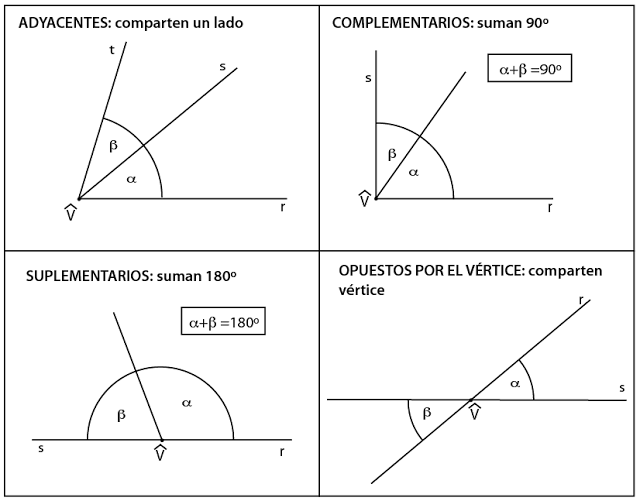
4.1. Clasificación de ángulos │según su relación
5. Ángulos entre rectas paralelas cortadas por una secante
Si una recta transversal corta a dos rectas paralelas:
- Ángulos alternos internos: son los ángulos que están entre las paralelas y a distinto lado de la transversal.
- Ángulos alternos externos: son los ángulos que están en la parte exterior de las paralelas y a distinto lado de la transversal.
- Ángulos correspondientes: son los que están del mismo lado de la transversal y en la misma posición respecto de cada paralela, pero uno es interno y el otro externo a las paralelas.
- Ángulos conjugados internos: son dos ángulos internos a las dos rectas paralelas y del mismo lado de la transversal.
- Ángulos conjugados externos: son dos ángulos externos a las dos rectas paralelas y del mismo lado de la transversal.
- Ángulos adyacentes: son dos ángulos que tienen el vértice común, un lado común que los separa y los otros dos lados en línea recta.
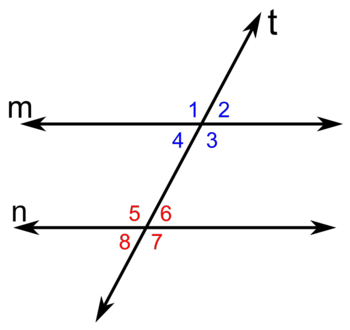
5.1. Ángulos entre paralelas y una secante
6. Elementos de la Circunferencia y del círculo.
Elementos de la circunferencia y el círculo
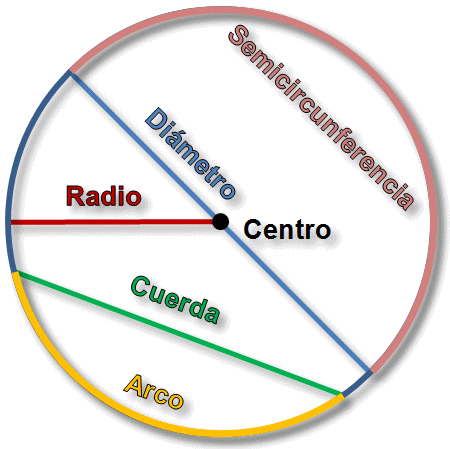
Los elementos del círculo son los siguientes:
1) Centro: es un punto interior equidistante de todos los puntos de la circunferencia.
2) Radio: es un segmento que une el centro con un punto de la circunferencia.
3) Diámetro: es el mayor segmento que une dos puntos de la circunferencia. Corresponde al doble del radio.
4) Arco: es un segmento curvilíneo de puntos que pertenecen a la circunferencia.
5) Cuerda: es un segmento que une dos puntos de la circunferencia. Las cuerdas con mayor longitud que podemos encontrar son los diámetros.
6) Secante: es una recta que corta la circunferencia en dos puntos.
7) Tangente: es una recta que toca la circunferencia en un solo punto.
7. Líneas notables, arco, perímetro y área aplicadas a actividades técnicas y tecnológicas del nuestro entorno
Perímetro de la circunferencia
El perímetro de la circunferencia es la medida de su longitud. Se puede obtener de dos maneras:
1).- Multiplicando “pi” (π) por diámetro
P = π x d
2.- Multiplicando dos veces “pi” por el radio
P = 2π x r
Cuando nos referimos al perímetro hablamos de unidades simples, ya que se mide sólo una dimensión: la longitud.
Área del circulo
El área del círculo es la medida de su superficie, como se trata de dos dimensiones, el resultado se da siempre en unidades cuadráticas o cuadradas.
El área del círculo se obtiene con la fórmula: pi por radio al cuadrado.
A = π x r²
8. NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (BIBLIOTECA KUAA)
NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA
ESCUELA DE MATEMÁTICAS UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN (LIBRO PROPORCIONADO POR LA BIBLIOTECA DE KUAA) https://ue.aprendiendomas.com.bo/pluginfile.php/290/mod_book/chapter/1533/%28%29%20-%20%28%29.pdf