EL MOVIMIENTO BIDIMENSIONAL EN EL ENTORNO DIARIO

Movimiento Parabólico o de Proyectiles

Conceptos básicos:

Es el movimiento de una partícula llamada proyectil, que describe como trayectoria una PARABOLA en el aire, cuando se la impulsa con una velocidad inicial a un ángulo de elevación.

Los tiros parabólicos son el caso más común de movimiento en dos dimensiones y combina dos tipos de movimiento en un solo:

El movimiento HORIZONTAL del tipo parabólico es rectilíneo uniforme continuo (MRU) ya que avanza espacios iguales en tiempos iguales.

El movimiento VERTICAL del tiro parabólico es uniforme acelerado (MUA) debido a la presencia de la aceleración gravitacional, formando una trayectoria de subida y otra de bajada.

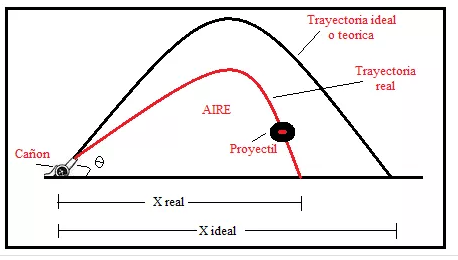
NOTA: En el estudio de los tiros parabólicos se considera el lanzamiento del objeto sin la resistencia del aire (como si fuera en el vacío).Aunque este es un factor muy importante que afecta la trayectoria real de vuelo, se complicaría demasiado el análisis el análisis de su movimiento  para efectos prácticos (su estudio corresponde a la balística física).

Formación de la trayectoria parabólica:

Sin gravedad, el proyectil seguiría una trayectoria rectilínea. Sin embargo, a causa de la gravedad, cae por debajo de esta línea la misma distancia vertical que caería si se le soltara desde el reposo.

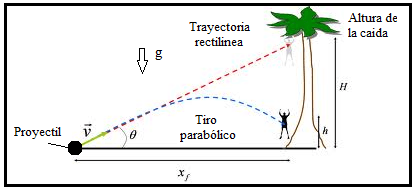
Efecto de la resistencia del aire en la trayectoria de un proyectil.

Elementos notables del tiro parabólico:

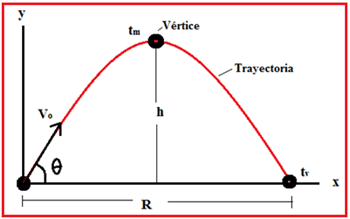
Partes

Vo = velocidad inicial del proyectil

θ  = ángulo de elevación

R = rango o alcance horizontal

H = altura máxima de elevación

tv = tiempo total de vuelo

tm = tiempo medio para llegar al punto más alto (vértice)

Características:

• La velocidad inicial (Vo) se la puede indicar en sus componentes vertical (Voy) horizontal (Vox).
• La velocidad horizontal (Vx) es constante para todo el recorrido, y en el punto más alto (vértice) toda la velocidad de la partícula  equivale a su velocidad horizontal:  Vo = Vox;  Voy = 0

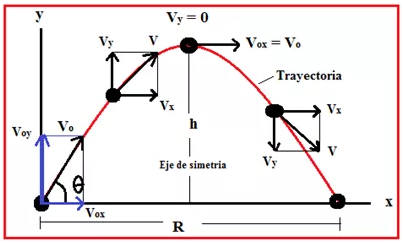
Descomposición de la velocidad inicial del proyectil, en sus componentes horizontal y vertical.

Si el punto de llegada está al mismo nivel de altura que el de partida, entonces:

• Los ángulos de elevación y de llegada son iguales. La rapidez inicial (V_o) es igual a la rapidez  final (V_f).
• El tiempo de subida t_m es igual al de bajada.

Todo esto se debe a que:

La parábola formada es simétrica respecto al eje vertical de su altura máxima .

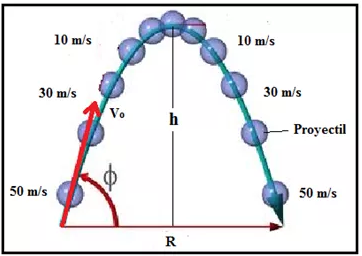
Simetría de la rapidez del proyectil, tanto en la subida como en la bajada.

Cuando se resuelva un caso de tiros parabólicos, se recomienda dividir los movimientos en horizontales y verticales, aplicando en cada uno las diferentes fórmulas del movimiento uniforme (MRU) y movimiento Acelerado (MUA), respectivamente:

Ecuación cartesiana

y = – (g /2. v_o².  Cos² θ ).x² + (tan θ).x

Nota: esta fórmula posee la forma y = -ax² + bx, que representa una gráfica en el plano cartesiano de la trayectoria teórica del tiro en  unidades de longitud. El signo (-) indica que la parábola se abre hacia abajo (como es obvio), ya que todos los tiros parabólicos tienen esa forma. El valor g = +9.8 m/s², si es el MKS. El ángulo θ no puede ser 90⁰ o múltiplo impar del mismo.

Ver más sobre movimiento parabólico