EL MOVIMIENTO BIDIMENSIONAL EN EL ENTORNO DIARIO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Ciencias Naturales: Física |
| Libro: | EL MOVIMIENTO BIDIMENSIONAL EN EL ENTORNO DIARIO |
| Impreso por: | Invitado |
| Fecha: | viernes, 7 de marzo de 2025, 03:28 |
1. Principio de independencia de los movimientos simultáneos.
En tu vida ordinaria observas gran cantidad de movimientos y muchos de ellos se producen en un plano. El salto de un niño, el lanzamiento de un objeto, una barca en un río, un avión en el aire, cualquier balón o pelota que se lanza para alcanzar un objetivo y un proyectil, son ejemplos de movimientos en dos dimensiones (el plano).
El movimiento más importante que vas a estudiar es el movimiento parabólico, que se produce cuando un objeto se mueve en las proximidades de la superficie terrestre con la aceleración de la gravedad. Grandes pensadores y científicos, como Aristóteles o Galileo Galilei, se ocuparon de este movimiento y escribieron tratados sobre los problemas de caída y tiro.
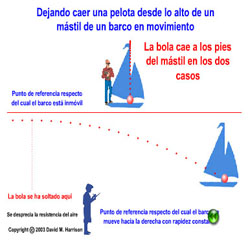
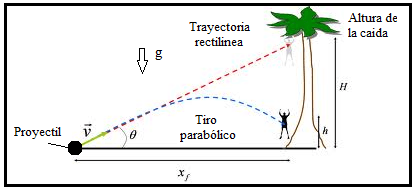
Ya has visto que la posición de un móvil depende del sistema de referencia elegido. El caso estudiado es la caída de una pelota desde lo alto de un mástil de un barco que avanza con movimiento uniforme y que impacta en la base del mástil: según el sistema de referencia la trayectoria es rectilínea o parabólica.
Galileo(1564-1642) explicó, mediante el estudio del movimiento de proyectiles, por qué la pelota cae en la base del mástil y no se queda atrás, como se creía hasta entonces: el movimiento de la pelota para el observador que se mueve con el velero es de caída libre, sin embargo para la observadora que está en la orilla es un movimiento parabólico (la trayectoria es una parábola), que puede considerarse como la superposición de un movimiento rectilíneo uniforme sobre la horizontal y de un movimiento de caída libre en la dirección vertical.
Ecuaciones vectoriales del movimiento
La posición, la velocidad y la aceleración del movimiento resultante es la suma de las posiciones, velocidades y aceleraciones de cada uno de los movimientos independientes.
En dos dimensiones son dos las coordenadas de posición que
varían, ya que la posición del móvil queda definida por el vector:
![]()
donde pueden variar las posiciones en los dos ejes, x e y.
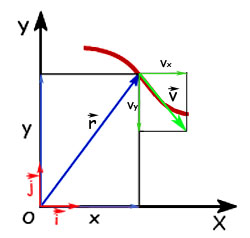
La posición, la velocidad y la aceleración están representadas por vectores y las componentes de cada vector en una dirección dada ( x o y), cumplen las ecuaciones estudiadas en el caso del movimiento rectilíneo, uniforme o acelerado
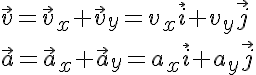
Más información sobre principio de independencia de movimientos
2. Movimiento semiparabolico
Movimiento semiparabólico
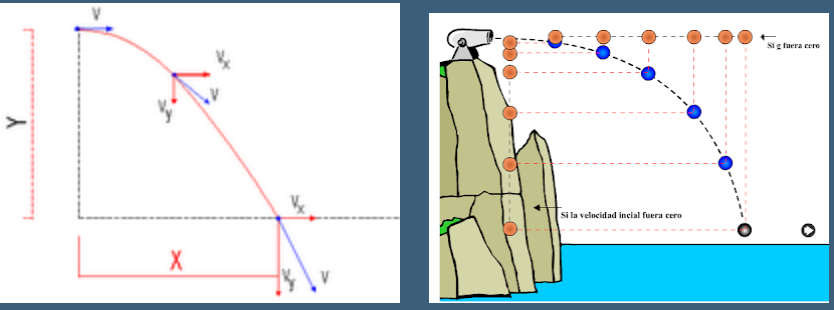
Es importante considerar durante todo el recorrido la aceleración debido a que la gravedad permanece constante y que el movimiento solo es de traslación.
- El movimiento horizontal del objeto es rectilíneo y uniforme ya que en esa dirección la acción de la gravedad es nula y consecuente, la aceleración también.
- En la dirección vertical sobre el objeto actúa la fuerza de gravedad que hace que el movimiento sea rectilíneo uniformemente acelerado, con la aceleración constante.
- Los cuerpos se lanzan horizontalmente desde cierta altura y con una velocidad inicial (Vi)
- El movimiento en "x" es independiente del movimiento en y.
- El tiempo de caída es variable que relaciona a los dos movimientos (MU y MUA)
3. Movimiento parabólico de proyectiles
Movimiento Parabólico o de Proyectiles
Conceptos básicos:
Es el movimiento de una partícula llamada proyectil, que describe como trayectoria una PARABOLA en el aire, cuando se la impulsa con una velocidad inicial a un ángulo de elevación.
Los tiros parabólicos son el caso más común de movimiento en dos dimensiones y combina dos tipos de movimiento en un solo:
El movimiento HORIZONTAL del tipo parabólico es rectilíneo uniforme continuo (MRU) ya que avanza espacios iguales en tiempos iguales.
El movimiento VERTICAL del tiro parabólico es uniforme acelerado (MUA) debido a la presencia de la aceleración gravitacional, formando una trayectoria de subida y otra de bajada.
NOTA: En el estudio de los tiros parabólicos se considera el lanzamiento del objeto sin la resistencia del aire (como si fuera en el vacío).Aunque este es un factor muy importante que afecta la trayectoria real de vuelo, se complicaría demasiado el análisis el análisis de su movimiento para efectos prácticos (su estudio corresponde a la balística física).
Formación de la trayectoria parabólica:
Sin gravedad, el proyectil seguiría una trayectoria rectilínea. Sin embargo, a causa de la gravedad, cae por debajo de esta línea la misma distancia vertical que caería si se le soltara desde el reposo.
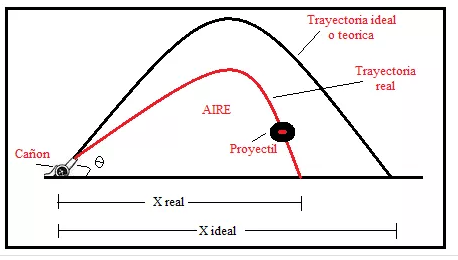
Efecto de la resistencia del aire en la trayectoria de un proyectil.
Elementos notables del tiro parabólico:
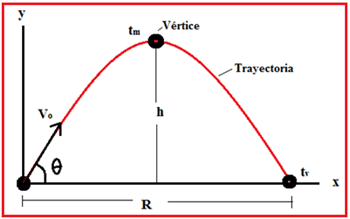
Partes
Vo = velocidad inicial del proyectil
θ = ángulo de elevación
R = rango o alcance horizontal
H = altura máxima de elevación
tv = tiempo total de vuelo
tm = tiempo medio para llegar al punto más alto (vértice)
Características:
- La velocidad inicial (Vo) se la puede indicar en sus componentes vertical (Voy) horizontal (Vox).
- La velocidad horizontal (Vx) es constante para todo el recorrido, y en el punto más alto (vértice) toda la velocidad de la partícula equivale a su velocidad horizontal: Vo = Vox; Voy = 0
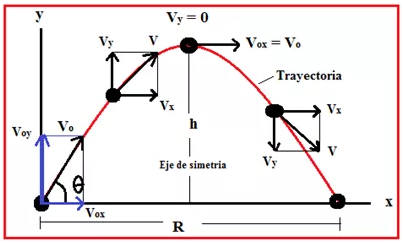
Descomposición de la velocidad inicial del proyectil, en sus componentes horizontal y vertical.
Si el punto de llegada está al mismo nivel de altura que el de partida, entonces:
- Los ángulos de elevación y de llegada son iguales. La rapidez inicial (Vo) es igual a la rapidez final (Vf).
- El tiempo de subida tm es igual al de bajada.
Todo esto se debe a que:
La parábola formada es simétrica respecto al eje vertical de su altura máxima .
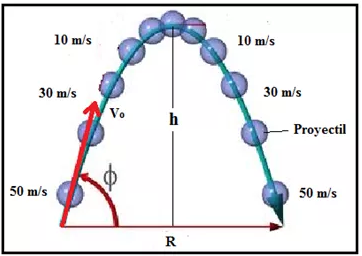
Simetría de la rapidez del proyectil, tanto en la subida como en la bajada.
Cuando se resuelva un caso de tiros parabólicos, se recomienda dividir los movimientos en horizontales y verticales, aplicando en cada uno las diferentes fórmulas del movimiento uniforme (MRU) y movimiento Acelerado (MUA), respectivamente:

Ecuación cartesiana
y = – (g /2. vo2. Cos2 θ ).x2 + (tan θ).x
Nota: esta fórmula posee la forma y = -ax2 + bx, que representa una gráfica en el plano cartesiano de la trayectoria teórica del tiro en unidades de longitud. El signo (-) indica que la parábola se abre hacia abajo (como es obvio), ya que todos los tiros parabólicos tienen esa forma. El valor g = +9.8 m/s2, si es el MKS. El ángulo θ no puede ser 900 o múltiplo impar del mismo.
Ver más sobre movimiento parabólico
4. Análisis de la velocidad, alcance máximo y altura máxima.
Información detallada de velocidad.alcance máximo y altura máxima