PROGRESIONES Y ANÁLISIS COMBINATORIO APLICADOS EN DIFERENTES CONTEXTOS
x
6. Combinaciones: sin repetición y con repetición
6.2. Triángulo de Pascal y número combinatorio.
El triángulo de Pascal o Tartaglia
El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito.
HISTORIA
El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy anterior al de estos dos matemáticos . Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII).
El que se le asocie el nombre del filósofo, matemático Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. Lo deTartaglia (1500-1557) viene porque el italiano fue de los primeros que lo publicaron en Europa.
Triángulo de Pascal y números Combinatorios
Los números del triángulo de Pascal coinciden con
los números combinatorios.
El número combinatorio Cm n
(n sobre m) se encuentra en el triángulo en la fila n+1,
en el lugar m+1.
El número combinatorio Cm
n (n sobre m) que representa
el número de grupos de m elementos que pueden hacerse de entre
un conjunto de n (por ejemplo, (4 sobre 2) nos da el número
de parejas distintas que podrían hacerse en un grupo de cuatro
personas), se encuentra en el triángulo en la fila n+1,
en el lugar m+1.
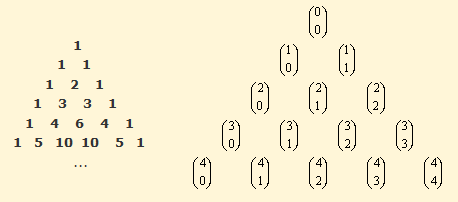
Podemos saber que el número de parejas posibles que decíamos
antes es 6 si miramos el tercer número de la quinta fila.
Esto hace que el triángulo sea útil como representación de estos
números, y proporciona una buena forma de intuir sus propiedades.
Por el contrario, a la fórmula de los números combinatorios
se le puede dar el carácter de fórmula general del triángulo
para saber, sin necesidad de construir todas las filas anteriores,
cuál es el número que ocupa un lugar determinado,:
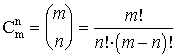
Más información de Triángulo de pascal y número combinatorios