PROGRESIONES Y ANÁLISIS COMBINATORIO APLICADOS EN DIFERENTES CONTEXTOS
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Matemáticas |
| Libro: | PROGRESIONES Y ANÁLISIS COMBINATORIO APLICADOS EN DIFERENTES CONTEXTOS |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 09:31 |
Descripción
x
Tabla de Contenidos
- 1. Progresiones Aritméticas, Geométricas y sus propiedades.
- 2. Principio fundamental del conteo.
- 3. Factorial de un número
- 4. Permutaciones: sin repetición, con repetición y circulares.
- 5. Variaciones y con repetición
- 6. Combinaciones: sin repetición y con repetición
- 7. Aplicación de la permutación, variación y repetición en actividades del contexto
1. Progresiones Aritméticas, Geométricas y sus propiedades.
Progresiones aritméticas y geométricas
Toda secuencia ordenada de números reales recibe el nombre de sucesión. Dentro del grupo de sucesiones existen dos particularmente interesantes por el principio de regularidad que permite sistematizar la definición de sus propiedades: las progresiones aritméticas y geométricas.
- Progresiones aritméticas
Una progresión aritmética es una clase de sucesión de números reales en la que cada término se obtiene sumando al anterior una cantidad fija predeterminada denominada diferencia. Llamando d a esta diferencia, el término general de la progresión an , que ocupa el número de orden n en la misma, se puede determinar a partir del valor del primero de los términos, a1.
an = a1 + (n - 1) d.
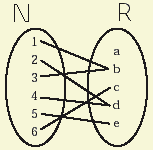
Las sucesiones (por ejemplo, las progresiones aritméticas y geométricas)
pueden verse como correspondencias unívocas entre el conjunto de los
números naturales N y el de los reales R.
Suma de los términos de una progresión aritmética
Para determinar la suma de un número finito de términos de una progresión aritmética, denotada por a1, a2, a3, ..., an-2, an-1, an, basta con considerar el principio de que los pares de términos a1 y an, a2 y an-1, a3 y an-2, etcétera, son equidistantes, de manera que todos estos pares suman una misma cantidad.
Generalizando esta consideración, se tiene que la suma de todos los términos de una progresión aritmética es igual a:
![]()
Interpolación de términos en una progresión aritmética
Entre cada dos términos a y b de una progresión aritmética es posible interpolar otros m términos, llamados medios diferenciales, de manera que todos ellos integren una nueva progresión aritmética (con m + 2 términos) donde a y b sean los extremos.
La diferencia de esta progresión se determinará con arreglo a la siguiente fórmula:
- Progresiones geométricas
Otra forma común de sucesión es la constituida por las llamadas progresiones geométricas. Estas progresiones se definen como aquellas en las que cada término se obtiene multiplicando el anterior por un valor fijo predefinido que se conoce como razón.
El término general an de una progresión geométrica puede escribirse como:
an = a1 ×
rn-1
Suma y producto de los términos de una progresión geométrica
La suma de n términos consecutivos de una progresión geométrica puede
calcularse a partir de cualquiera de las siguientes expresiones:
![]()
Esta fórmula sólo es válida si r ¹ 1, ya que si r = 1 todos los términos de la progresión serían iguales, y la suma sería Sn = a1 × n.
Cuando r > 1, la progresión crece indefinidamente y la suma de sus términos tiende a infinito. En cambio, si r < 1, cada término será menor que el anterior, y la progresión se irá acercando a 0 conforme aumente el número de sus términos. Cuando | r | < 1, puede demostrarse que la suma se convierte en:
![]()
Por otra parte, es fácil obtener que el producto de los n primeros términos de una progresión geométrica es igual a:
![]()
Interpolación de términos en una progresión geométrica
Entre dos términos a y b de una progresión geométrica es
posible intercalar m términos, denominados medios geométricos o proporcionales,
tales que todos ellos (los m + 2 términos resultantes) constituyan una nueva
progresión geométrica de razón r determinada como:
![]()
Ver más sobre progresión aritmetica
Ver más sobre progresión Geométrica
2. Principio fundamental del conteo.
Principio Fundamental de Conteo
TECNICAS DE CONTEO
El principio fundamental en el proceso de contar ofrece un método general para contar el número de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento B puede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a n1 x n2.
26 x 25 x 10 x 9 x 8 = 468000
Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades. Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc.
* La tecnica de la suma o Adicion
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de. El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro. Si un evento E1 puede suceder de n1 maneras diferentes, el evento E2 puede ocurrir de n2 maneras diferentes, y así sucesivamente hasta el evento Ep el cual puede ocurrir de np maneras diferentes, entonces el total de maneras distintas en que puede suceder el evento “ocurren E1 y E2…..y Ep” es igual a producto.
Se dispone de 3 vías para viajar de C1 a C2 y de 4 vías para viajar de C2 a C1. ¿De cuántas formas se puede organizar el viaje de ida y vuelta de C1 a C2.Respuesta: (3)(4)=12
M = 2 x 4 x 2 = 16 maneras
N = 3 x 2 x 2 = 12 maneras
W = 1 x 2 x 1 = 2 maneras
M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora
Si una primera operación puede realizarse de m maneras y una segunda operación de n maneras, entonces una operación o la otra pueden efectuarse de:
PRINCIPIO DE PERMUTACION:
A
diferencia de la formula de la multiplicación, se la utiliza para
determinar el numero de posibles arreglos cuando solo hay un solo grupo
de objetos. Permutación: un arreglos o posición de r objetos
seleccionados de un solo grupo de n objetos posibles. Si nos damos
cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la
formula que se utiliza para contar el numero total de permutaciones
distintas es:
Ejemplo: ¿Como se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
Donde: n= número total de objetos r= número de objetos seleccionados!= factorial, producto de los números naturales entre 1 y n.
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador. !
PRINCIPIO DE COMBINACION:
En una permutación, el orden de los objetos de cada posible resultado es diferente.
Si el orden de los objetos no es importante, cada uno de estos resultados se
denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo
formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el
equipo hay dos funciones diferentes, entonces si importa el orden, los
resultados serán permutaciones. Por el contrario si en el equipo no hay
funciones definidas, entonces no importa el orden y los resultados serán
combinaciones. Los resultados en ambos casos son los siguientes:
Permutaciones: AB, AC, BA, CA, BC, CB
Combinaciones: AB, AC, BC
Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n
objetos sin importar el orden.
La fórmula de combinaciones es:
n C r = n! r! (n – r)!
Ejemplo: En una
compañía se quiere establecer un código de colores para identificar cada
una de las 42 partes de un producto. Se quiere marcar con 3 colores de
un total de 7 cada una de las partes, de tal suerte que cada una tenga
una combinación de 3 colores diferentes. ¿Será adecuado este código de
colores para identificar las 42 partes del producto?
Usando la fórmula de combinaciones:
3. Factorial de un número
¿Qué es la función factorial?
La función factorial se representa con un signo de exclamación “!” detrás de un número. Esta exclamación quiere decir que hay que multiplicar todos los números enteros positivos que hay entre ese número y el 1.
Por ejemplo:
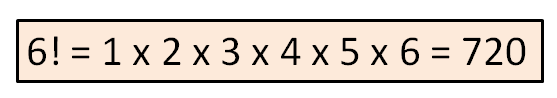
A este número, 6! le llamamos generalmente “6 factorial”, aunque también es correcto decir “factorial de 6”.
En tu calculadora podrás ver una tecla con “n!” o “x!”. Esta tecla te servirá para calcular directamente la factorial del número que quieras.
Algunos ejemplos de factoriales
Vamos a ver algunos ejemplos más de factoriales:
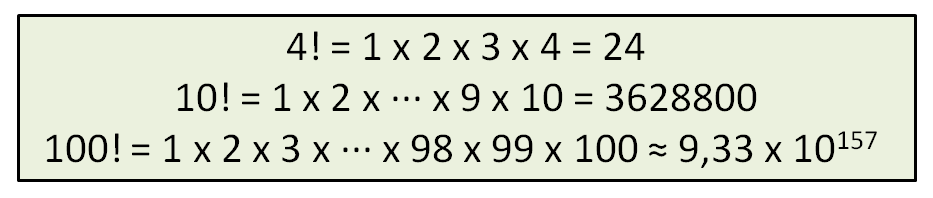
Como ves, 100! es enorme…
Y, ¿qué hacemos con los números más pequeños? 1 factorial es, lógicamente, 1, ya que multiplicamos 1 x 1:
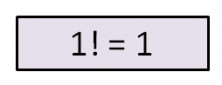
Pero, ¿cómo podemos calcular el 0 factorial? Bueno, esto no tiene sentido cuando aplicamos la norma de que hay que multiplicar todos los números enteros positivos entre el 0 y el 1, ya que 0 x 1 es 0.
Al final, por convenio se ha acordado que lo más útil es que el 0 factorial sea igual a 1. Así que recuerda:
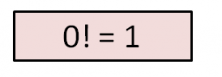
¿Para qué podemos utilizar los factoriales?
Los números factoriales se utilizan sobre todo en combinatoria, para calcular combinaciones y permutaciones. A través de la combinatoria, los factoriales también se suelen utilizar para calcular probabilidades.
Vamos a ver un ejemplo sencillo de problema en el que podemos aplicar los factoriales:

En este problema nos están pidiendo lo que se llama una permutación, es decir, que averigüemos todas las maneras posibles en las que estas 4 cartas se pueden combinar teniendo en cuenta el orden en el que las colocamos.
Si comenzamos haciendo todas las filas posibles comenzando con el as de diamantes, podemos hacer 6 combinaciones:
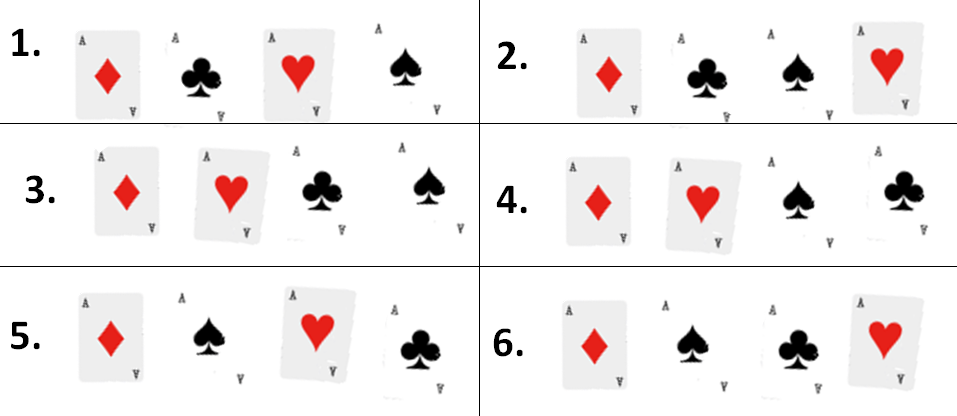
También tendremos 6 combinaciones posibles con el de tréboles, con el de corazones y con el de picas, es decir, 6 combinaciones empezando con cada una de las 4 cartas: 4 x 6 = 24

Utilizando la función factorial, podríamos haber resuelto el problema de forma mucho más sencilla:
Pensamos en una sola combinación de los 4 ases:
– Cuando hemos elegido el primero, ya solo nos quedan 3 para elegir
– Cuando hemos elegido el segundo, ya solo nos quedan 2 para elegir
– Cuando hemos elegido el tercero, ya solo nos queda 1 para elegir
Por lo tanto, todas las combinaciones posibles serán 4 x 3 x 2 x 1.
O lo que es lo mismo, 4! = 24
Más información sobre factorial de un número
3.1. Propiedades de los factoriales.
Propiedades de los factoriales

Ver más....
3.2. Doble factorial.
Explicación sencilla y completa de doble factorial
4. Permutaciones: sin repetición, con repetición y circulares.
¿Cómo se forman?. Para construir las permutaciones sin repetición de un conjunto de n elementos, tenemos que construir grupos de n elementos sin que se puedan repetir. Se trata entonces de hacer lo mismo que se ha hecho con las variaciones sin repetición de orden n a partir de un conjunto de n elementos.
De dos elementos. A = {1,2}. V2,2 = 2. Las dos permutaciones son: 12 y 21.
De tres elementos. A = {1,2,3}. V3,3 = 6. Las seis permutaciones son: 123 , 132 , 213 , 231 , 312 y 321.
De cuatro elementos. A = {1,2,3,4}. V4,4 = 24. Las veinticuatro permutaciones son: 1234 , 1243 , 1324 , 1342 , 1423 , 1432 , 2134 , 2143 , 2314 , 2341 , 2413 , 2431 , 3124 , 3142 , 3214 , 3241 , 3412 , 3421 , 4123 , 4132 , 4213 , 4231 , 4312 , 4321.
¿Cuántas hay?. Dada la relación existente entre permutaciones y variaciones sin repetición, se puede deducir que:
Pn = Vn,n = n • (n-1) • • • (n-n+1) = n!.
¿Cómo se forman?. Vamos a hacerlo con un ejemplo. Construir todos los números de seis cifras posibles utilizando dos veces el número uno y cuatro veces el número dos.
Para hacerlo de una forma ordenada vamos a utilizar el diagrama de árbol como se hace en la siguiente escena.
¿Cuántas hay?. Hemos calculado el número de permutaciones con repetición de seis elementos en las que el primer elemento se repite dos veces y el segundo se repite cuatro veces: P62,4 . Si el elemento que se repite dos veces fuera distinto, obtendríamos a partir de cada permutación, 2! permutaciones distintas. De la misma forma si el elemento que se repite cuatro veces fuera distinto, obtendríamos también 4! permutaciones distintas, obteniendo de esta forma todas las permutaciones posibles con seis elementos distintos, por tanto:
Con esta otra escena se pueden construir las permutaciones con repetición hasta de cinco elementos en todos los casos posibles de repeticiones.
Permutaciones circulares
Las permutaciones circulares son un caso particular de las permutaciones.
Se utilizan cuando los elementos se han de ordenar "en círculo", (por ejemplo, los comensales en una mesa), de modo que el primer elemento que "se sitúe" en la muestra determina el principio y el final de muestra.
![]()
Ejemplos
1. Calcular las permutaciones circulares de 7 elementos.
PC7= (7 − 1)! = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
2. ¿De cuántas formas distintas pueden sentarse ocho personas alrededor de una mesa redonda?
![]()
Más sobre permutaciones sin repetición
Más sobre permutaciones con repetición
Más sobre permutaciones circulares
5. Variaciones y con repetición
Se llaman variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que:
No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Sí importa el orden.
Sí se repiten los elementos
Ejemplos
1. ¿Cuántos números de tres cifras se puede formar con los dígitos: 1, 2, 3, 4, 5 ?
m = 5 n = 3
No entran todos los elementos. De 5 dígitos entran sólo 3
Sí importa el orden. Son números distintos el 123, 231, 321
Sí se repiten los elementos
![]()
2. ¿Cuántos números de tres cifras se puede formar con los dígitos: 0, 1, 2, 3, 4, 5?
m = 6 n = 3
Tenemos que separar el número en dos bloques:
El primer bloque, de un número, lo puede ocupar sólo uno de 5 dígitos porque un número no comienza por cero (excepto los de las matriculas, los de la lotería y otros casos particulares).
m = 5 n = 1
El segundo bloque, de dos números, lo puede ocupar cualquier dígito.
m = 6 n = 2
3. ¿Cuántas quinielas de una columna han de rellenarse para asegurarse el acierto de los 15 resultados?
m = 3 n = 15 m < n
Sí entran todos los elementos. En este caso el número de orden es mayor que el número de elementos
Sí importa el orden
Sí se repiten los elementos
![]()
6. Combinaciones: sin repetición y con repetición
Combinaciones sin repetición





Más sobre combinaciones sin repetición
Combinaciones con repetición

ver más sobre combinaciones con repetición
6.1. Número combinatorio
Números combinatorios
Las agrupaciones combinatorias que sólo consideran la esencia de los grupos formados y no su orden, llamadas combinaciones, han constituido una rama específica dentro de la especialidad del análisis combinatorio, con múltiples usos en diversos campos. La expresión numérica de tales combinaciones recibe el nombre de número combinatorio o coeficiente binómico.
Coeficientes binómicos
Se define número combinatorio o coeficiente binómico como el valor numérico de las combinaciones ordinarias (sin repetición) de un conjunto de n elementos tomados en grupos de r, siendo n y r dos números enteros y positivos tales que n ³ r. Matemáticamente, un número combinatorio se expresa como:
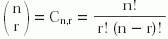
Propiedades de los números combinatorios
Los números combinatorios presentan algunas propiedades muy interesantes que justifican el amplio uso que se hace de ellos en algunas ramas científicas:
- Primera propiedad de los números combinatorios:
- Segunda propiedad de los números combinatorios.
Otras propiedades generales de los números combinatorios son las siguientes:
- Cualquier número sobre 0 es igual a 1.
- Todo número sobre sí mismo es igual a 1.
- Un número sobre 1 es siempre igual al número.
Más información sobre números combinatorios
6.2. Triángulo de Pascal y número combinatorio.
El triángulo de Pascal o Tartaglia
El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un 1 en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. Se supone que los lugares fuera del triángulo contienen ceros, de forma que los bordes del triángulo están formados por unos. Aquí sólo se ve una parte; el triángulo continúa por debajo y es infinito.
HISTORIA
El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy anterior al de estos dos matemáticos . Se tienen referencias que datan del siglo XII en China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático chino Yang Hui (siglo XIII), así como el poeta persa Omar Khayyam (siglo XII).
El que se le asocie el nombre del filósofo, matemático Pascal (1623-1662) se debe a que el francés escribió el primer tratado sobre el triángulo. Lo deTartaglia (1500-1557) viene porque el italiano fue de los primeros que lo publicaron en Europa.
Triángulo de Pascal y números Combinatorios
Los números del triángulo de Pascal coinciden con
los números combinatorios.
El número combinatorio Cm n
(n sobre m) se encuentra en el triángulo en la fila n+1,
en el lugar m+1.
El número combinatorio Cm
n (n sobre m) que representa
el número de grupos de m elementos que pueden hacerse de entre
un conjunto de n (por ejemplo, (4 sobre 2) nos da el número
de parejas distintas que podrían hacerse en un grupo de cuatro
personas), se encuentra en el triángulo en la fila n+1,
en el lugar m+1.
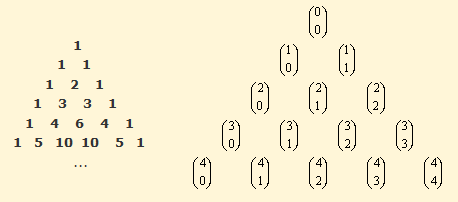
Podemos saber que el número de parejas posibles que decíamos
antes es 6 si miramos el tercer número de la quinta fila.
Esto hace que el triángulo sea útil como representación de estos
números, y proporciona una buena forma de intuir sus propiedades.
Por el contrario, a la fórmula de los números combinatorios
se le puede dar el carácter de fórmula general del triángulo
para saber, sin necesidad de construir todas las filas anteriores,
cuál es el número que ocupa un lugar determinado,:
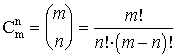
Más información de Triángulo de pascal y número combinatorios
6.3. Binomio de Newton
BINOMIO DE NEWTON
Vamos a deducir la fórmula que
nos permitirá elevar a cualquier potencia de exponente natural, n, un binomio.
Esto es la forma de obtener![]() Para ello veamos como se van
desarrollando las potencias de (a+b)
Para ello veamos como se van
desarrollando las potencias de (a+b)
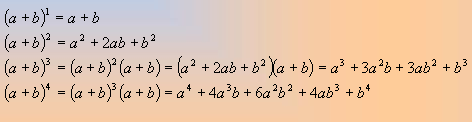
Observando los coeficientes de cada polinomio resultante vemos que siguen esta secuencia

Esto es el triángulo de Tartaglia que se obtiene escribiendo en filas los números combinatorios desde los de numerador 1.
O sea que cada uno de esos números corresponde al valor de un número combinatorio así:

Podemos observar que cada fila empieza y termina por 1, que los números que aparecen forman una fila simétrica, o sea el primero es igual al último, el segundo igual al penúltimo, etc., y cada número es la suma de los dos que tiene encima.
Por otra parte en cualquier momento podemos hallar el valor de un número combinatorio cualquiera recordando que se calculan por la siguiente fórmula:
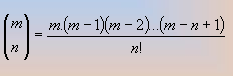

Por otra parte, observando las potencias de (a+b) de nuevo vemos que las potencias de a empiezan elevadas a n, va disminuyendo uno a uno hasta llegar a cero. A los exponentes de b les ocurre lo contrario.
Con lo que ya tenemos podemos calcular directamente la siguiente potencia de (a+b), sus coeficientes serán la fila quinta del triángulo de Tartaglia.
![]()
Y ya podemos escribir la fórmula general del llamado binomio de Newton
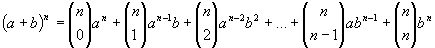
que también se puede escribir de forma abreviada así
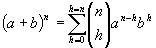
Más sobre Binomio de Nweton
7. Aplicación de la permutación, variación y repetición en actividades del contexto
Cómo saber aplicar una permutación, variación y repeteción