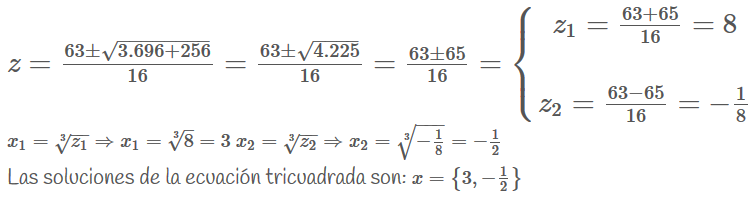FUNCIONES Y ECUACIONES EN LA PRODUCTIVIDAD.
4. Ecuaciones de 2do grado y grado superior de una variable.
ECUACIONES DE GRADO SUPERIOR A DOS
Las ecuaciones de grado superior a dos son ecuaciones de tercer, cuarto o grado superior sólo pueden resolverse en algunos casos con los conocimientos elementales.
Supongamos que la ecuación está dada en la forma P(x) = 0.
La resolución se basa en la descomposición del polinomio P(x) en factores. Esto lo haremos generalmente utilizando la regla de Ruffini. Hecho esto, basta igualar a cero cada uno de los factores y resolver las ecuaciones de primer grado y de segundo grado resultantes.
Para que las ecuaciones de tercer grado (o grado superior) se puedan resolver a nivel elemental deben tener alguna raíz entera, que se encuentra entre los divisores del término independiente.
Ejemplo:
Después igualamos cada factor a cero y despejamos la x. De ahí obtenemos todas las soluciones:
Por lo tanto las soluciones son: x = {-1, 1, 2}
Casos especiales de ecuaciones de grado superior a 2:
Existen casos especiales de ecuaciones de grado superior a 2:
-Ecuaciones bicuadradas
-Ecuaciones tricuadradas
Este tipo de ecuaciones son ecuaciones que se pueden reducir a una ecuación de segundo grado.
Ecuaciones bicuadradas
Se llaman ecuaciones bicuadradas a las ecuaciones de la forma
Es decir, las ecuaciones bicuadradas son ecuaciones de cuarto grado que carecen de términos de grado impar.
Las ecuaciones bicuadradas también se pueden escribir así:
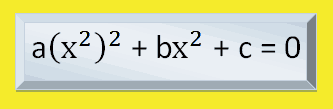
ecuación bicuadrada
Una ecuación bicuadrada se puede reducir a una ecuación de segundo grado mediante las sustituciones:
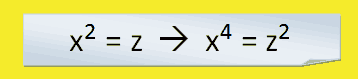
Sustituciones para reducir una ecuación bicuadrada a una ecuación de segundo grado
Entonces la ecuación de segundo grado resultante es esta:
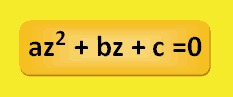
Ecuación de segundo grado obtenida a partir de una ecuación bicuadrada
Si llamamos z1 y z2 a las soluciones de esta última ecuación, las soluciones de la ecuación bicuadrada serán:
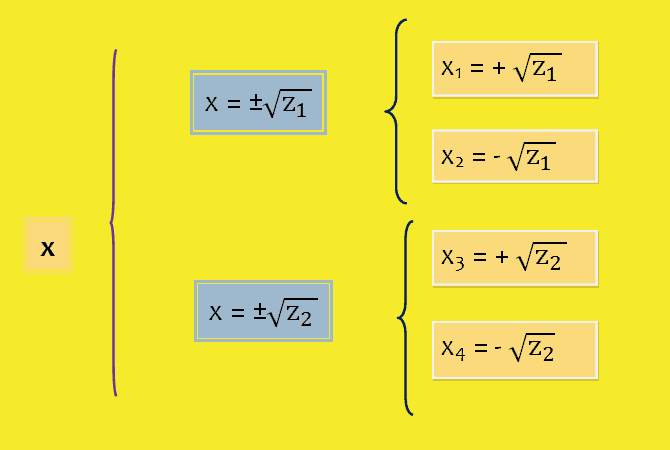
Soluciones de una ecuación bicuadrada
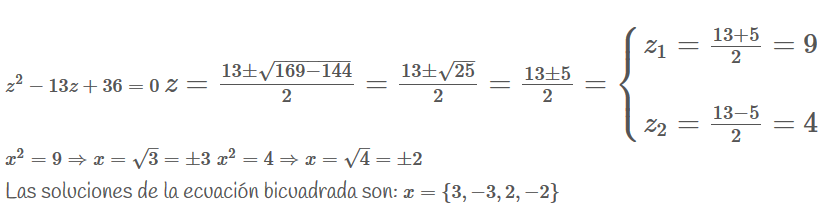
Ecuaciones tricuadradas
Se llaman ecuaciones tricuadradas a las ecuaciones de la forma ![]()
Es decir, las ecuaciones tricuadradas son ecuaciones de sexto grado que carecen de términos de grado quinto, cuarto y segundo.
Las ecuaciones tricuadradas también se pueden escribir así:
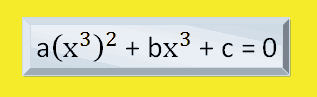

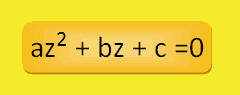
Ejemplo:
Transformamos esta ecuación bicuadrada en una ecuación de segundo grado: