FUNCIONES Y ECUACIONES EN LA PRODUCTIVIDAD.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Matemáticas |
| Libro: | FUNCIONES Y ECUACIONES EN LA PRODUCTIVIDAD. |
| Impreso por: | Invitado |
| Fecha: | jueves, 3 de abril de 2025, 05:21 |
Tabla de Contenidos
- 1. Funciones y ecuaciones lineales de dos incógnitas.
- 2. Estudio, análisis y resolución de matrices y determinantes y el método de Cramer.
- 3. Funciones cuadráticas y su representación gráfica a través del programa GeoGebra.
- 4. Ecuaciones de 2do grado y grado superior de una variable.
- 5. Ecuaciones de segundo grado o grado superior con valor absoluto
1. Funciones y ecuaciones lineales de dos incógnitas.
Un sistema lineal de dos ecuaciones con dos incógnitas es un sistema lineal de ecuaciones formado por sólo dos ecuaciones que admite un tratamiento particularmente simple, junto con el caso trivial de una ecuación lineal con una única incógnita, es el caso más sencillo posible de sistemas de ecuaciones, y que permiten su resolución empleando técnicas básicas del álgebra cuando los coeficientes de la ecuación se encuentran sobre un cuerpo (sobre un anillo la solución no es tan sencilla).
Una infinidad de problemas pueden ser resueltos con un sistema de dos ecuaciones. Veamos las distintas formas en las que se pueden encontrar sus soluciones.
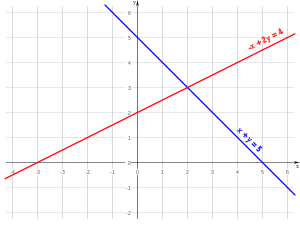
Tipos de solución
Consideremos un sistema como el siguiente:
En un sistema de ecuaciones se pueden dar los siguientes casos:
Sí admite soluciones.
La compatibilidad de un sistema se determina a partir del determinante de la matriz 2x2 que constituye el sistema o equivalentemente de los cocientes de la primera ecuación y la segunda.
Sistema compatible determinado
Sí admite un número finito de soluciones; en el caso de dos ecuaciones lineales con dos incógnitas, si el sistema es determinado solo tendrá una solución. Su representación gráfica son dos rectas que se cortan en un punto; los valores de x e y de ese punto son la solución al sistema.
Un sistema lineal de dos ecuaciones con dos incógnitas es compatible determinado cuando:
En el ejemplo de la figura, dado el sistema:
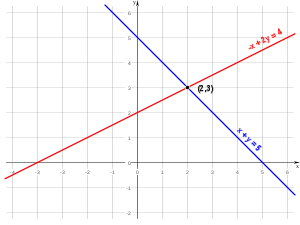
Podemos ver, que:
Lo que da lugar a que las dos rectas se corten en un punto, de valores
Sistema compatible indeterminado
El sistema admite un número infinito de soluciones; su representación gráfica son dos rectas coincidentes. Las dos ecuaciones son equivalentes y una de ellas se puede considerar como redundante: cualquier punto de la recta es solución del sistema.
Un sistema lineal de dos ecuaciones con dos incógnitas es indeterminado si:
Por ejemplo con el sistema:
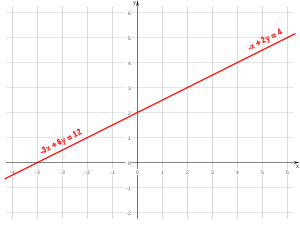
Se puede ver:
Con lo que podemos decir que la primera ecuación multiplicada por tres da la segunda ecuación, por lo tanto no son dos ecuaciones independientes, sino dos formas de expresar la misma ecuación.
Tomando una de las ecuaciones, por ejemplo la primera, tenemos:
Tomando la x como variable independiente, y la y como variable dependiente, según la expresión anterior, asignando valores a x obtendremos el correspondiente de y, cada par (x, y), así calculado será una solución del sistema, pudiendo asignar a x cualquier valor real.
Sistema incompatible
El sistema no admite ninguna solución. En este caso, su representación gráfica son dos rectas paralelas y no tienen ningún punto en común porque no se cortan. El cumplimiento de una de las ecuaciones significa el incumplimiento de la otra y por lo tanto no tienen ninguna solución en común.
Un sistema lineal de dos ecuaciones con dos incógnitas es incompatible si
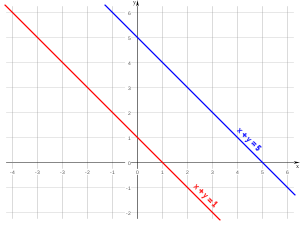
Por ejemplo, dado el sistema:
La igualdad:
Determina la proporcionalidad entre las incógnitas, dos rectas paralelas, pero la diferente proporcionalidad con los términos independientes determina un corte con el eje y disiento, y dos rectas paralelas no se cortan en ningún punto. Dando lugar a la incompatibilidad de las soluciones.
Análisis de tipos
Para poder determinar si, un sistema de dos ecuaciones con dos incógnitas, corresponde a uno de esos casos, podemos ver, según lo visto anteriormente, el siguiente criterio, partiendo del sistema:
Podemos aplicar el siguiente árbol de decisión, para determinar el tipo de sistema que es:
Para ello, comparamos en primer lugar la relación entre los coeficientes de las incógnitas, si la relación entre los coeficientes de la x y la y es el mismo, el sistema es compatible indeterminado o incompatible, si este coeficiente también es igual a la relacione entre los términos independientes el sistema es compatible indeterminado, y si es distinto en incompatible. Si la relación entre los coeficientes de la x y la y son distintos el sistema es compatible determinado.
Este criterio es equivalente al análisis de los determinantes de las ecuaciones, aplicado a un sistema de dos ecuaciones.
1.1. Sistemas de ecuaciones lineales y no lineales.
Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.


Pero no siempre existe solución, o bien, pueden existir infinitas soluciones. Si hay una única solución (un valor para cada incógnita, como en el ejemplo anterior) se dice que el sistema es compatible determinado. No hablaremos de los otros tipos ya que en esta página sólo se estudian los sistemas determinados.
Para resolver un sistema (compatible determinado) necesitamos tener al menos tantas ecuaciones como incógnitas.
En esta página resolvemos sistemas de dos ecuaciones (lineales) con dos incógnitas mediante
los métodos que describimos a continuación, que se basan en la obtención de una ecuación de primer grado.
Métodos de resolución
Método de sustitución: consiste en despejar o aislar una de las incógnitas (por ejemplo, ) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, . Una vez resuelta, calculamos el valor de sustituyendo el valor de que ya conocemos
Método de reducción: consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita.
Método de igualación: consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una ecuación con una sola incógnita.
No olvidemos que si multiplicamos una ecuación por un número distinto de
0, la ecuación inicial y la obtenida son equivalentes. Esto quiere
decir que ambas ecuaciones tienen las mismas soluciones y, por tanto,
podemos trabajar con una u otra.
Usaremos esta propiedad con frecuencia en el método de reducción.
Más información sobre ecuaciones lineales y no lineales
1.2. Sistema de ecuaciones de tres ecuaciones lineales con tres incógnitas.
Se pueden interpretar estos sistemas como un conjunto de tres planos en el espacio real tridimensional![]()
En algunos casos no habrá solución, en otros habrá infinitas (una línea de puntos solución) y en otros habrá una única solución
Para resolver este tipo de sistemas se aplicará reducción, de forma que cada ecuación tenga una incógnita menos que la anterior. Por ello, se utilizará el método de Gauss.
Ejemplo
Resolver:
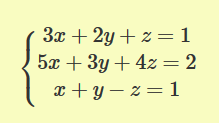
1) Se coloca como primera ecuación la que tenga 1
Si no hubiera ninguna se pone como primera ecuación la que
tenga
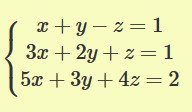
2) Se utiliza el método de reducción para las ecuaciones
3) Se repite el mismo procedimiento con
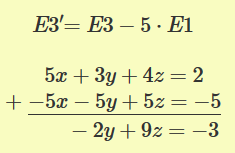
4) Con las nuevas ecuaciones
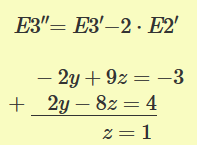
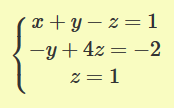

Nota: Es habitual el uso de notación matricial para la resolución de este tipo de problemas. El enunciado del ejemplo anterior se escribiría:
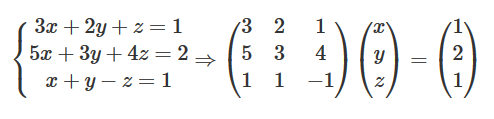
Además, dicha notación ofrece ciertas ventajas para el análisis del sistema, ya que el cálculo del determinante puede ser útil para tener una idea de las soluciones que se obtendrán.
- Si el determinante no es nulo, el sistema es compatible determinado, es decir, tiene una única solución.
- Si el determinante es nulo, el sistema puede ser:
- Compatible indeterminado: si tiene ecuaciones proporcionales y, por lo tanto, infinitas soluciones.
Incompatible: No tiene soluciones.
1.3. Gráfica de Sistema de Ecuaciones en el plano cartesiano.
Graficando sistemas de ecuaciones lineales
Recuerda que una ecuación lineal se grafica como una recta, que indica que todos los puntos de una recta son soluciones de la ecuación lineal. Existe un número infinito de soluciones. Si tenemos un sistema de ecuaciones lineales, la solución del sistema es el valor que hace válidas todas las ecuaciones. Para dos variables y dos ecuaciones, este es el punto donde las gráficas se intersectan. Las coordenadas de este punto serán la solución para las dos variables en las dos ecuaciones.
Sistemas de Ecuaciones
La solución de un sistema de ecuaciones es el valor o valores que hacen válidas a todas las ecuaciones en el sistema. Las gráficas de las ecuaciones del sistema te dicen cuántas soluciones existen para ese sistema. Observa las imágenes siguientes. Cada una muestra dos rectas que forman el sistema de ecuaciones.
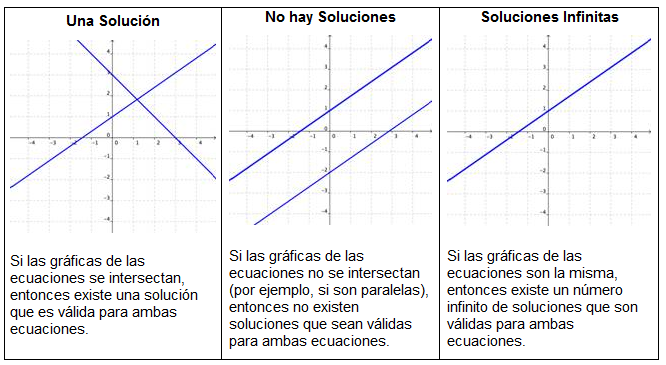
Cuando las rectas se intersectan, el punto de intersección es el único punto que las dos gráficas tienen en común, Entonces las coordenadas de ese punto son la solución de las dos variables usadas en las ecuaciones. Cuando las rectas son paralelas, no hay soluciones y a veces las dos ecuaciones se grafican como la misma recta, en tal caso tenemos un número infinito de soluciones.
Algunos términos especiales son usados a veces para describir tipos de sistemas.
Los siguientes términos se refieren a cuántas soluciones tiene el sistema.
- Cuando un sistema tiene una solución (las gráficas de las ecuaciones se intersectan), es un sistema consistente de ecuaciones lineales y las ecuaciones son independientes.
- Cuando el sistema no tiene solución (las gráficas de las ecuaciones no se intersectan), es un sistema inconsistente de ecuaciones lineales y las ecuaciones son independientes.
- Si las rectas son la misma (las gráficas se intersectan en todos los puntos), es un sistema consistente de ecuaciones lineales y las ecuaciones son dependientes. Esto es, cualquier solución de una ecuación debe ser también una solución de la otra, por lo que las ecuaciones dependen una de la otra.
Los siguientes términos se refieren a si un sistema tiene soluciones.
- El sistema es un sistema consistente de ecuaciones lineales cuando tiene soluciones.
- El sistema es un sistema inconsistente de ecuaciones lineales cuando no tiene soluciones.

2. Estudio, análisis y resolución de matrices y determinantes y el método de Cramer.
Método Cramer
El método Cramer es una manera de resolver un sistema lineal, pero sólo se puede utilizar en sistemas de resolución que el número de ecuaciones y el número de incógnitas son iguales.

Por lo tanto, para resolver un sistema lineal de n incógnitas en las ecuaciones para su resolución debe calcular el determinante (D) de la ecuación del sistema incompleto y luego vuelva a colocar los términos constantes en cada columna y calcular sus respectivos determinantes y así aplicar la regla de Cramer que dice: los valores de las incógnitas se calculan de la siguiente manera:
x 1 = D1 D x 2 = D2 D x 3 = D3 … x n = Dn D D
Véase el siguiente ejemplo de cómo al aplicar la regla de Cramer este:
Dado el sistema lineal de resolverlo podemos utilizar la regla de Cramer como tiene tres ecuaciones y tres incógnitas, es decir, el número de incógnitas es igual al número de ecuaciones.
Podemos encontrar matriz incompleta de este sistema lineal que se denominará A. Ahora calcular su determinante de ser representado por D. D = 1 + 6 + 2 + 3 – 1 + 4 D = 15.
Ahora tenemos independiente reemplazar la primera columna de la matriz a, formando de este modo una segunda matriz que está representado por Ax .
Ahora calcular su determinante representado por Dx Dx = 8 + 4 + 3 + de 2 – 8 + 6 Dx = 15 . Nosotros sustituimos los términos constantes en la segunda columna de la matriz incompleta que forman la matriz Ay
Ahora calcular su determinante dy. dy = -3 + 24 + 4 – 9 – 16 de 2 + dy = 30 Sustitución del sistema de términos independientes en la tercera columna de la matriz incompleta formará la matriz Az. Ahora calculamos su determinante representado por Dz.
3. Funciones cuadráticas y su representación gráfica a través del programa GeoGebra.
Como Graficar Funciones en Geogebra
4. Ecuaciones de 2do grado y grado superior de una variable.
ECUACIONES DE GRADO SUPERIOR A DOS
Las ecuaciones de grado superior a dos son ecuaciones de tercer, cuarto o grado superior sólo pueden resolverse en algunos casos con los conocimientos elementales.
Supongamos que la ecuación está dada en la forma P(x) = 0.
La resolución se basa en la descomposición del polinomio P(x) en factores. Esto lo haremos generalmente utilizando la regla de Ruffini. Hecho esto, basta igualar a cero cada uno de los factores y resolver las ecuaciones de primer grado y de segundo grado resultantes.
Para que las ecuaciones de tercer grado (o grado superior) se puedan resolver a nivel elemental deben tener alguna raíz entera, que se encuentra entre los divisores del término independiente.
Ejemplo:
Después igualamos cada factor a cero y despejamos la x. De ahí obtenemos todas las soluciones:
Por lo tanto las soluciones son: x = {-1, 1, 2}
Casos especiales de ecuaciones de grado superior a 2:
Existen casos especiales de ecuaciones de grado superior a 2:
-Ecuaciones bicuadradas
-Ecuaciones tricuadradas
Este tipo de ecuaciones son ecuaciones que se pueden reducir a una ecuación de segundo grado.
Ecuaciones bicuadradas
Se llaman ecuaciones bicuadradas a las ecuaciones de la forma
Es decir, las ecuaciones bicuadradas son ecuaciones de cuarto grado que carecen de términos de grado impar.
Las ecuaciones bicuadradas también se pueden escribir así:
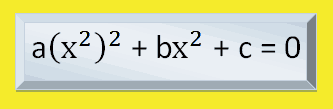
ecuación bicuadrada
Una ecuación bicuadrada se puede reducir a una ecuación de segundo grado mediante las sustituciones:
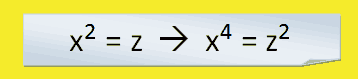
Sustituciones para reducir una ecuación bicuadrada a una ecuación de segundo grado
Entonces la ecuación de segundo grado resultante es esta:
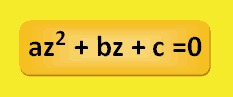
Ecuación de segundo grado obtenida a partir de una ecuación bicuadrada
Si llamamos z1 y z2 a las soluciones de esta última ecuación, las soluciones de la ecuación bicuadrada serán:
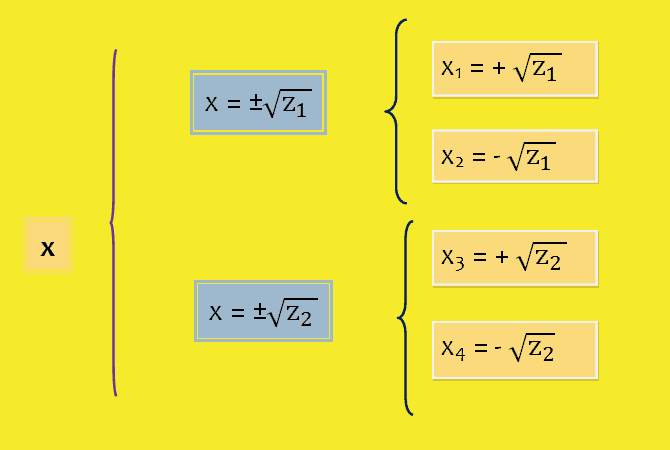
Soluciones de una ecuación bicuadrada
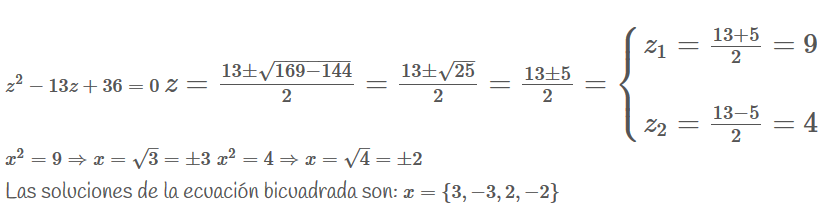
Ecuaciones tricuadradas
Se llaman ecuaciones tricuadradas a las ecuaciones de la forma ![]()
Es decir, las ecuaciones tricuadradas son ecuaciones de sexto grado que carecen de términos de grado quinto, cuarto y segundo.
Las ecuaciones tricuadradas también se pueden escribir así:
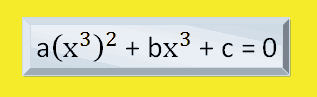

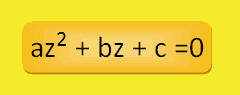
Ejemplo:
Transformamos esta ecuación bicuadrada en una ecuación de segundo grado:
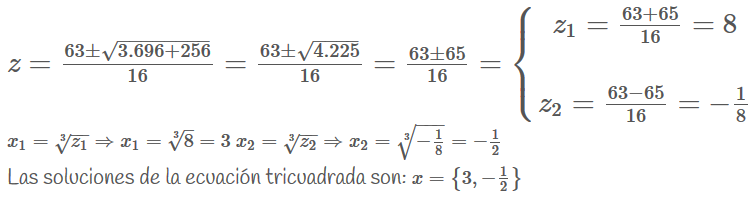
5. Ecuaciones de segundo grado o grado superior con valor absoluto
Ecuaciones con valor absoluto
El conjunto de soluciones de una ecuación con valor absoluto viene dado por la siguiente relación:
|x| = a ⇔ x = a o x = - a
dados x , a ∈ R y a > 0 :
Ejemplos de ecuaciones con valor absoluto
1) |2x + 6| = 0
De acuerdo con lo expuesto anteriormente, tenemos que:
|2x + 6| = 0 ⇔ 2x + 6 = 0 ⇔ 2x = - 6 ⇔ x = - 3
2) |2x - 5| = 4
De acuerdo con definición, tenemos dos posibilidades:
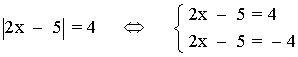
• |2x - 5| = 4 ⇔ 2x - 5 = 4 ⇔ 2x = 9 ⇔ x = 9/2
• |2x - 5| = 4 ⇔ 2x - 5 = - 4 ⇔ 2x = 1 ⇔ x = 1/2
Por tanto, el conjunto solución es:
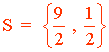
3) |x2 - 2| = 2 - 3x
Por otro lado, tenemos dos posibilidades para la igualdad:
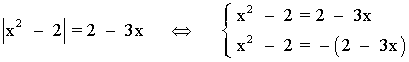
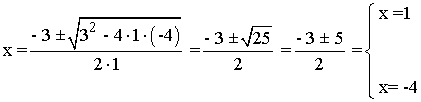
• x2 - 2 = - (2 - 3x) = - 2 + 3x ⇔ x2 - 3x = 0 ⇔ x ( x - 3) = 0
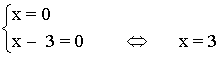
Comprobamos si las soluciones cumplen la ecuación:
x = 1: |12 - 2| = 2 - 3·1 ⇔ 1 ≠ -1 x = 1 no es solución
Hacemos lo mismo para el resto de soluciones.
x = - 4 es solución
x = 0 es solución
x = 3 no es solución
Por tanto, el conjunto solución es:
S = { -4 , 0 }
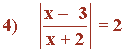

ecuaciones con valor absoluto
ejemplo
5.1. Aplicación de las ecuaciones en problemas planteados a partir de actividades en general.
Problema Aplicación Ecuaciones de Primer Grado
Problema con ECUACIONES CUADRÁTICAS