FUNCIONES Y ECUACIONES EN LA PRODUCTIVIDAD.
5. Ecuaciones de segundo grado o grado superior con valor absoluto
Ecuaciones con valor absoluto
El conjunto de soluciones de una ecuación con valor absoluto viene dado por la siguiente relación:
|x| = a ⇔ x = a o x = - a
dados x , a ∈ R y a > 0 :
Ejemplos de ecuaciones con valor absoluto
1) |2x + 6| = 0
De acuerdo con lo expuesto anteriormente, tenemos que:
|2x + 6| = 0 ⇔ 2x + 6 = 0 ⇔ 2x = - 6 ⇔ x = - 3
2) |2x - 5| = 4
De acuerdo con definición, tenemos dos posibilidades:
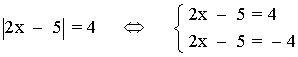
• |2x - 5| = 4 ⇔ 2x - 5 = 4 ⇔ 2x = 9 ⇔ x = 9/2
• |2x - 5| = 4 ⇔ 2x - 5 = - 4 ⇔ 2x = 1 ⇔ x = 1/2
Por tanto, el conjunto solución es:
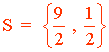
3) |x2 - 2| = 2 - 3x
Por otro lado, tenemos dos posibilidades para la igualdad:
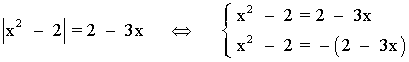
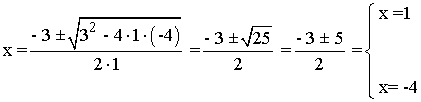
• x2 - 2 = - (2 - 3x) = - 2 + 3x ⇔ x2 - 3x = 0 ⇔ x ( x - 3) = 0
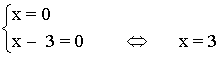
Comprobamos si las soluciones cumplen la ecuación:
x = 1: |12 - 2| = 2 - 3·1 ⇔ 1 ≠ -1 x = 1 no es solución
Hacemos lo mismo para el resto de soluciones.
x = - 4 es solución
x = 0 es solución
x = 3 no es solución
Por tanto, el conjunto solución es:
S = { -4 , 0 }
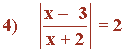

ecuaciones con valor absoluto
ejemplo