MATEMÁTICA FINANCIERA Y SOFTWARE Y LENGUAJES DE PROGRAMACIÓN

En esta sección se revisarán los elementos básicos que se van a utilizar para escribir programas. Esto supone que los alumnos ya saben programar, y es sólo un resumen y una ordenación de conceptos. La notación utilizada es la del lenguaje Java, pero los conceptos son más generales y se aplican a muchos otros lenguajes similares.

Datos

Los programas representan la información que manejan mediante valores llamados "constantes", y dichos valores se almacenan en "variables".

Variables

Nótese que la secuencia "//" indica el comienzo de un comentario, el cual se extiende hasta el final de la línea.

Constantes

Instrucciones Elementales

Asignación

Esta es la instrucción más simple, que permite modificar el valor de una variable:

Ejemplos:

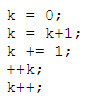
Las tres últimas son abreviaturas. La notación "+=" permite evitar repetir el lado izquierdo de la asignación. Las dos últimas incrementan el valor de la variable en 1, pero difieren respecto del valor retornado. En el primer caso (preincremento) se incrementa primero y luego se retorna el valor resultante. El el segundo caso (postincremento) se incrementa después, y se retorna el valor previo de la variable.

Salida

Instrucciones Compuestas

Estas instrucciones se forman agrupando a otras instrucciones, ya sean elementales o compuestas, usando las reglas de secuencia, alternación (if) e iteración (while).

Secuencia de instrucciones

Un grupo de instrucciones escritas una a continuación de la otra se ejecutan en ese mismo orden:

También es posible agrupar las instrucciones entre llaves para que sean equivalentes a una sola instrucción:

Ejemplo:

Instrucciones condicionales

Nota: No existe el "endif". Si lo que se desea ejecutar en cada caso es más de una instrucción, hay que escribirlas encerradas entre llaves.

Ejemplo:

La línea destacada no es una instrucción real del lenguaje, es sólo una forma de dejar pendiente esa parte del programa. Más adelante se podrá "refinar" esa seudo-instrucción definiendo:

La línea destacada no es una instrucción real del lenguaje, es sólo una forma de dejar pendiente esa parte del programa. Más adelante se podrá "refinar" esa seudo-instrucción definiendo:

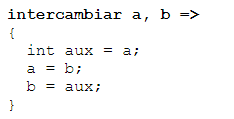
Si se efectúa la sustitución del texto refinado en lugar del que se había escrito originalmente, resulta un texto de programa refinado que cumple con las reglas del lenguaje. Para ayudar a la auto-documentación del programa, se puede conservar la seudo-instrucción como comentario:

Ejemplo: Encontrar el máximo entre un conjunto de variables

Realizando las sustituciones respectivas, se obtiene la siguiente versión "refinada":

Nota: En este caso, las llaves no son realmente necesarias, pero pueden utiizarse si ayudan a la claridad del programa.

Este enfoque de solución tiene la desventaja que es difícil de generalizar. Por ejemplo, el programa que encuentra el máximo de cuatro variables tiene aproximadamente el doble de líneas que éste, y por lo tanto el tamaño del programa va creciendo exponencialmente. Además no hay forma de escribir un programa para un número de variables que no sea conocido a priori.

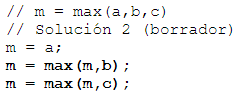
Sustituyendo las seudo-instrucciones, resulta:

Con cada instrucción que se ejecuta, el estado del proceso cambia. Para entender lo que está sucediendo en el programa, puede resultar útil intercalar comentarios que describan lo que sabemos que se cumple después de cada instrucción:

Ese tipo de comentarios se llaman afirmaciones (assertions), y en casos más complejos son fundamentales para entender lo que está sucediendo en un proceso.

La generalización para encontrar el máximo de cuatro o más variables es directa, y en cada caso requiere sólo agregar dos líneas al programa. Más adelante se verá una versión para un número variable de datos.

Instrucción iterativa

La forma general es:

La instrucción se ejecuta en forma reiterada mientras la condición sea verdadera.

Cada vez que se intenta iniciar una nueva iteración (incluyendo la primera vez que ello ocurre) el programa se encuentra en un estado I llamado el invariante del ciclo.

En general, al escribir un ciclo, se debe establecer la validez inicial del invariante, a través de una inicialización. El objetivo del ciclo es llegar a un estado final F. En cada iteración se debe, además, preservar la validez del invariante.

Ejemplo:

Considere el problema de encontrar el máximo de un número variable de datos, almacenados en un arreglo a[1], ..., a[n]. Para verlo en forma iterativa, imagine un proceso en que los datos se van examinando uno a uno, comparándolos con el máximo encontrado hasta el momento. De esta manera, si en un instante dado ya se han examinado los datos hasta a[k], entonces se conoce el máximo hasta esa variable.

Esta última afirmación se deduce del hecho que al terminar el ciclo se sabe que el invariante sigue siendo verdadero, pero la condición del ciclo es falsa. En estricto rigor, la afirmación que podríamos hacer ahí es

de la cual se deduce la señalada al final del programa.

¿Cómo escribir un ciclo?

1. Encontrar un invariante adecuado. Para esto, a menudo es conveniente "relajar" la meta (estado final) al que se desea llegar. Por ejemplo, si se desea obtener:

se puede re-escribir esta condición separándola en dos condiciones que se puedan satisfacer independientemente:


Esto, que puede parecer ocioso, es muy útil, porque a continuación se relaja la exigencia de esta condición, haciendo que se cumpla la primera parte, pero dejando que la segunda se satisfaga con "k<=n".

2. Escribir la inicialización, la cual debe asegurar que el invariante se cumpla antes de empezar a iterar.

3. Encontrar la condición de término. Esto se obtiene de comparar "qué le falta" al invariante para ser igual al estado final.

4. Escribir el cuerpo del ciclo, el cual debe:
          - conseguir que el proceso avance, de modo que termine algún día, y
          - preservar el invariante.
Estos dos últimos objetivos suelen ser contrapuestos. Al efectuar un avance en el proceso, los valores de las variables cambian, con el resultado que a menudo se deja de satisfacer el invariante. Por lo tanto, el resto del cuerpo del ciclo se suele dedicar a tratar de recuperar la validez del invariante.