MATEMÁTICA FINANCIERA Y SOFTWARE Y LENGUAJES DE PROGRAMACIÓN
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Matemáticas |
| Libro: | MATEMÁTICA FINANCIERA Y SOFTWARE Y LENGUAJES DE PROGRAMACIÓN |
| Impreso por: | Invitado |
| Fecha: | jueves, 30 de enero de 2025, 23:37 |
1. Matemática financiera básica
Matemáticas financieras, se entiende por ello, una rama de las matemáticas que estudia las variaciones cuantificables que se producen en los capitales (aportes en dinero) financieros durante el transcurso del tiempo.

Clasificaciones de las matemáticas financieras
Dentro de las matemáticas se estudian las operaciones financieras simples y las complejas, la definición es la siguiente:
- Simple: Analiza los dineros que provienen de un solo capital (Denominados intereses).
- Complejas: Analiza los dineros que provienen de más de un capital (Denominadas Rentas).
Otra clasificación es la aplicación de las operaciones de la aplicación, donde dependiendo la temporalidad, pueden existir dos grandes principios:
- Principio de Capitalización: Cuando tengo flujos al día de hoy y quiero saber cuánto tendré a futuro
- Principio de Descuento: Cuanto flujo tendré a futuro y quisiera saber cuánto vale el día de hoy.
El propósito de poder analizar esta corriente, se repunta por el principio que el dinero pierde valor en el tiempo, ¿Se ha dado cuenta que comprar un paquete de papas fritas antes valía $200 y ahora vale $500?, alguna gente lo considera como “Inflación”, pero no necesariamente es solo eso. También existe otro factor que se denomina “Costo de Oportunidad”, donde este dice que es lo que yo sacrifico por disponer de los flujos en un concepto y no otro. Ejemplo: “Usted posee $100.000 el día de hoy, de lo cual los puede gastar en hacer una fiesta, o sino invertir y en dos meses más, recibir $105.000”, si usted elige la primera opción, el costo de oportunidad sería dejar de ganar $5.000, si elige la segunda opción, el costo de oportunidad consiste en no hacer la celebración. Por lo cual las matemáticas financieras nacen para analizar flujos y dependiendo la decisión que quiera tomar, poder añadir o quitar este concepto que denominaremos momentáneamente como “Suma de la inflación y costo de oportunidad”.
Todo lo anteriormente señalado, se denomina “Pérdida de valor en el tiempo”, y cumple con ciertos principios elementales:
- Ante dos capitales de igual monto en distintos momentos, se preferirá el que sea de tiempo más cercano.
- Ante dos capitales de distinto importe pero en un mismo momento, se preferirá el de monto más alto.
Todos estos principios y bases, se utilizan para comparar flujos que por defecto del tiempo no pueden ser comparables. Si usted tuviera $100.000 el día de hoy y $100.000 en 2 años más, nominalmente siguen siendo $100.000, pero el valor es más alto hoy, dado que lo que puede adquirir hoy es más de lo que podrá con el mismo valor nominal a futuro. Por ende las matemáticas financieras cumplen ese rol.
Introduccion matematicas financieras
1.1. Interés simple
Se denomina interés simple a aquella tasa aplicada sobre un capital origen que permanece constante en el tiempo y no se añade a periodos sucesivos.
En otras palabras, el interés simple se calcula para pagos o cobros sobre el capital dispuesto inicialmente en todos los periodos considerados, mientras que el interés compuesto va sumando los intereses al capital para producir nuevos intereses.
El interés puede ser pagado o cobrado, sobre un préstamo que paguemos o sobre un depósito que cobremos. La condición que diferencia al interés compuesto del interés simple, es que mientras en una situación de interés compuesto los intereses devengados se van sumando y produciendo nueva rentabilidad junto al capital inicial, en un modelo de interés simple solo se calculan los intereses sobre el capital inicial prestado o depositado.
Así pues, puesto que los intereses no se van incorporando al capital, estos quedan devengados y se reciben al final del periodo.
Fórmula para calcular el interés simple
La fórmula que utilizaremos para calcular el interés simple será la siguiente:
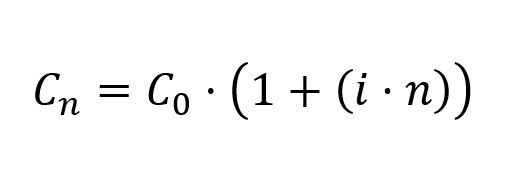
Siendo C0 el capital inicial prestado, i la tasa de interés, n el periodo de tiempo considerado y Cn el capital final resultante.
Ejemplo de interés simple
Un ejemplo práctico para determinar el interés simple con un capital inicial de 1.000€ y una tasa de interés del 5% en un periodo de 5 años:
| Período | Cantidad al inicio del período | Intereses del período | Cantidad que se adeuda al final del período |
|---|---|---|---|
| 1 | 1.000 € | (1.000 *5%)= 50 € | 1.000 + 50 €= 1.050 € |
| 2 | 1.000 € | (1.000 *5%)= 50 € | 1.000 + 50 €= 1.050 € |
| 3 | 1.000 € | (1.000 *5%)= 50 € | 1.000 + 50 €= 1.050 € |
| 4 | 1.000 € | (1.000 *5%)= 50 € | 1.000 + 50 €= 1.050 € |
| 5 | 1.000 € | (1.000 *5%)= 50 € | 1.000 + 50 €= 1.050 € |
Interés simple con ejemplos resueltos
1.2. Monto, capital, tasa de interés y tiempo
Interés Simple: Es el que proporciona un capital sin agregar rédito vencido, dicho de otra manera es el que devenga un capital sin tener en cuenta los intereses anteriores.
Monto Simple (M): Se define como el valor acumulado del capital. Es la suma del capital más el interés, su ecuación es: M = C + I
Capital (C): También se le denomina valor actual o presente del dinero, inversión inicial, hacienda.
Tipo de interés: Interés simple y compuesto
Plazo o tiempo: Es el que normalmente se especifica en el documento o contrato puede ser cualquier unidad de tiempo; días, meses, años, etc.
Descuento: Es la disminución que se hace a una cantidad por pagarse antes de su vencimiento. Es el cobro anticipado de un valor que se vence en el futuro.
Tipos de descuento:
- Descuento simple a una tasa de interés: El valor presente C de una cantidad M con vencimiento en una fecha posterior, puede ser interpretado como el valor descontado de M. A este tipo de descuento se le conoce como descuento racional. Dr = M – C
- Descuento simple a una tasa de descuento: La tasa de descuento se define como la razón del descuento dado en la unidad se tiempo (en este caso un año) al capital sobre el cual esta dado el descuento. La tasa de descuento anual se expresa como un porcentaje. Conocido también como descuento bancario. Fórmula: D = M d t
Fecha focal: Es la fecha que se elige para hacer coincidir el valor de las diferentes operaciones, dicho de otra manera es la fecha que se escoge para la equivalencia
Ecuaciones equivalentes: Es aquel que nos sirve para conocer el monto del capital, invertido en un tiempo especifico y con una cierta tasa de interés. El valor total de las operaciones de adeudo debe ser igual a las operaciones de pago. De las cuales tres de las operaciones serán las que se conocerán su valor y uno permanecerá en incógnita la cual será despejada, después de esto se conocerá su valor y se equilibrará la ecuación.
1.3. Tipos de interés simple (clasificación)
Interés Simple: Características
Las principales características del Interés Simple son:
- El capital inicial se mantiene igual durante toda la operación.
- El interés es el mismo para cada uno de los períodos de la operación.
- La tasa de interés se aplica sobre el capital invertido o capital inicial.
Interés Simple: Fórmula
A continuación se muestra la fórmula del interés simple:
VF = VA (1 + n * i)
- VF = Valor Futuro
- VA = Valor Actual
- i = Tasa de interés
- n = Periodo de tiempo
Podemos obtener el interés que produce un capital con la siguiente fórmula:
I = C * i * n
Ejemplo: Si queremos calcular el interés simple que produce un capital de 1.000.000 pesos invertido durante 5 años a una tasa del 8% anual. El interés simple se calculará de la siguiente forma:
I = 1.000.000 * 0,08 * 5 = 400.000
Si queremos calcular el mismo interés durante un periodo menor a un año (60 días), se calculará de la siguiente forma:
Periodo: 60 días = 60/360 = 0,16 I = 1.000.000 * 0,08 * 60/360 = 13.333
Interés Compuesto: ¿Qué es?
En este tipo de interés, los intereses que se consiguen en cada periodo se van sumando al capital inicial, con lo que se generan nuevos intereses. En este tipo de interés a diferencia del interés simple, los intereses no se pagan a su vencimiento, porque se van acumulando al capital. Por esta razón, el capital crece al final de cada uno de los periodos y el interés calculado sobre un capital mayor también crece.
Interés Compuesto: Características
Las principales características del Interés Compuesto son:
- El capital inicial aumenta en cada periodo debido a que los intereses se van sumando.
- La tasa de interés se aplica sobre un capital que va variando.
- Los intereses son cada vez mayores.
Interés Compuesto: Fórmula
A continuación se muestra la fórmula del Interés Compuesto y sus componentes:
VA = VF (1 + i) ^n
- VF = Valor Futuro
- VA = Valor Actual
- i = Tasa de interés
- n = Periodo de tiempo
Matemáticas Financieras Interés compuesto
1.4. Descuento bancario o simple
Existen operaciones financiera donde se calculan los intereses sobre el valor final durante toda la duración de una transacción. Es decir cuando una persona toma dinero prestado de un banco, por lo general se descuenta, es decir el interés o Descuento, se rebaja al inicio del periodo del préstamo en lugar de añadirlo al final.
La tasa de interés y descuento simple se utilizan normalmente para periodos cortos, máximo hasta tres o cinco años.
El Descuento Bancario es; por Io general, el interés simple ordinario pagado por adelantado. Casi siempre se deduce del importe del préstamo, recibiendo el deudor únicamente el saldo.
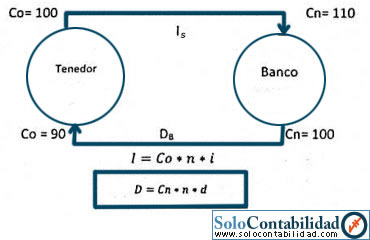
Dónde:
D = Descuento Bancario o Descuento Simple
n = Tiempo o Plazo
d = Tasa de descuento
Cn = Capital Final
El Valor Presente resulta ser la diferencia entre el Valor Final y el descuento bancario, es decir:

Ejemplo 1: Hallar el descuento Simple sobre una deuda de $ 1.500 con vencimiento en 9 meses a una tasa de descuento del 6% ¿Cuál es el valor presente de la deuda?

Respuesta: el valor de la deuda es de $ 1432,50
1.5. Ecuación de valor
Para poder entender lo que son las ecuaciones de valor, para que nos sirven y cómo entenderlas, es necesario, en primer lugar, entender el comportamiento del dinero a través del tiempo. Constantemente escuchamos hablar de la inflación, la cual no es otra cosa que un tipo de interés; en efecto, la inflación en realidad es la tasa de interés con la cual el dinero cambia de poder adquisitivo. Esto no significa que a medida que transcurre el tiempo las cosas son más caras, significa que a medida que pasa el tiempo el dinero pierde poder adquisitivo. Imagínate el precio de unas papas fritas al transcurrir el tiempo, como lo muestra la siguiente gráfica, a la que llamaremos gráfica de tiempo
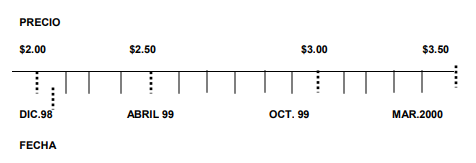
Como puedes observar, sigues adquiriendo el mismo producto, pero con diferente
cantidad de dinero, de ahí los conceptos del valor actúalo y valor futuro del dinero.
Si te ubicas en la gráfica, en octubre de 1999 los $3.00 son el valor actual en ese
momento, mientras que los, mientras que los $3.50 serían el valor futuro en marzo
del 2000 para el mismo producto.
Cuando se realiza una gráfica de tiempo, las unidades en que se divide
dependerán de las unidades en las que éste dado el interés del cual se hable.
Veamos esto en un ejemplo:
Se desea saber el valor futuro de $500.00 después de dos años, si se sabe que la
tasa de interés es de 14% trimestral simple.
Con la tasa de interés está dada por trimestre, la gráfica se traza en las mismas
unidades de tiempo es decir, trimestres.
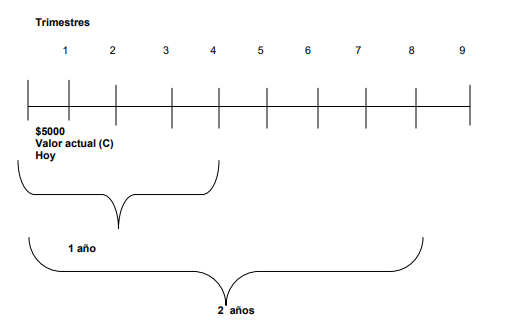
Para encontrar el valor futuro de los $500.00 hay que trasladarlos en el tiempo 8
trimestres más adelante (como se ve en la gráfica); en la definición de monto
encontramos que también es llamado valor futuro, y tomando en consideración los
datos tenemos (tiempo, capital y tasa de interés), entonces:

Significa que el valor futuro en 8 trimestres (2 años) de $500.00 a una tasa del
14% trimestral simple es de $1,060.00
2. Nociones de programación Básica (Visual Basic)
En esta sección se revisarán los elementos básicos que se van a utilizar para escribir programas. Esto supone que los alumnos ya saben programar, y es sólo un resumen y una ordenación de conceptos. La notación utilizada es la del lenguaje Java, pero los conceptos son más generales y se aplican a muchos otros lenguajes similares.
Datos
Los programas representan la información que manejan mediante valores llamados "constantes", y dichos valores se almacenan en "variables".
Variables

Nótese que la secuencia "//" indica el comienzo de un comentario, el cual se extiende hasta el final de la línea.
Constantes

Instrucciones Elementales
Asignación
Esta es la instrucción más simple, que permite modificar el valor de una variable:
![]()
Ejemplos:
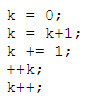
Las tres últimas son abreviaturas. La notación "+=" permite evitar repetir el lado izquierdo de la asignación. Las dos últimas incrementan el valor de la variable en 1, pero difieren respecto del valor retornado. En el primer caso (preincremento) se incrementa primero y luego se retorna el valor resultante. El el segundo caso (postincremento) se incrementa después, y se retorna el valor previo de la variable.
Salida
![]()
Instrucciones Compuestas
Estas instrucciones se forman agrupando a otras instrucciones, ya sean elementales o compuestas, usando las reglas de secuencia, alternación (if) e iteración (while).
Secuencia de instrucciones
Un grupo de instrucciones escritas una a continuación de la otra se ejecutan en ese mismo orden:

También es posible agrupar las instrucciones entre llaves para que sean equivalentes a una sola instrucción:

Ejemplo:

Instrucciones condicionales

Nota: No existe el "endif". Si lo que se desea ejecutar en cada caso es más de una instrucción, hay que escribirlas encerradas entre llaves.
Ejemplo:

La línea destacada no es una instrucción real del lenguaje, es sólo una forma de dejar pendiente esa parte del programa. Más adelante se podrá "refinar" esa seudo-instrucción definiendo:

La línea destacada no es una instrucción real del lenguaje, es sólo una forma de dejar pendiente esa parte del programa. Más adelante se podrá "refinar" esa seudo-instrucción definiendo:
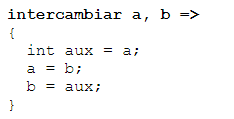
Si se efectúa la sustitución del texto refinado en lugar del que se había escrito originalmente, resulta un texto de programa refinado que cumple con las reglas del lenguaje. Para ayudar a la auto-documentación del programa, se puede conservar la seudo-instrucción como comentario:

Ejemplo: Encontrar el máximo entre un conjunto de variables

Realizando las sustituciones respectivas, se obtiene la siguiente versión "refinada":

Nota: En este caso, las llaves no son realmente necesarias, pero pueden utiizarse si ayudan a la claridad del programa.
Este enfoque de solución tiene la desventaja que es difícil de generalizar. Por ejemplo, el programa que encuentra el máximo de cuatro variables tiene aproximadamente el doble de líneas que éste, y por lo tanto el tamaño del programa va creciendo exponencialmente. Además no hay forma de escribir un programa para un número de variables que no sea conocido a priori.
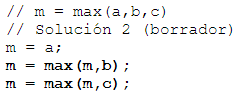
Sustituyendo las seudo-instrucciones, resulta:

Con cada instrucción que se ejecuta, el estado del proceso cambia. Para entender lo que está sucediendo en el programa, puede resultar útil intercalar comentarios que describan lo que sabemos que se cumple después de cada instrucción:

Ese tipo de comentarios se llaman afirmaciones (assertions), y en casos más complejos son fundamentales para entender lo que está sucediendo en un proceso.
La generalización para encontrar el máximo de cuatro o más variables es directa, y en cada caso requiere sólo agregar dos líneas al programa. Más adelante se verá una versión para un número variable de datos.
Instrucción iterativa
La forma general es:

La instrucción se ejecuta en forma reiterada mientras la condición sea verdadera.
Cada vez que se intenta iniciar una nueva iteración (incluyendo la primera vez que ello ocurre) el programa se encuentra en un estado I llamado el invariante del ciclo.
En general, al escribir un ciclo, se debe establecer la validez inicial del invariante, a través de una inicialización. El objetivo del ciclo es llegar a un estado final F. En cada iteración se debe, además, preservar la validez del invariante.
Ejemplo:
Considere el problema de encontrar el máximo de un número variable de datos, almacenados en un arreglo a[1], ..., a[n]. Para verlo en forma iterativa, imagine un proceso en que los datos se van examinando uno a uno, comparándolos con el máximo encontrado hasta el momento. De esta manera, si en un instante dado ya se han examinado los datos hasta a[k], entonces se conoce el máximo hasta esa variable.

Esta última afirmación se deduce del hecho que al terminar el ciclo se sabe que el invariante sigue siendo verdadero, pero la condición del ciclo es falsa. En estricto rigor, la afirmación que podríamos hacer ahí es
![]()
de la cual se deduce la señalada al final del programa.
¿Cómo escribir un ciclo?
1. Encontrar un invariante adecuado. Para esto, a menudo es conveniente "relajar" la meta (estado final) al que se desea llegar. Por ejemplo, si se desea obtener:
se puede re-escribir esta condición separándola en dos condiciones que se puedan satisfacer independientemente:
Esto, que puede parecer ocioso, es muy útil, porque a continuación se relaja la exigencia de esta condición, haciendo que se cumpla la primera parte, pero dejando que la segunda se satisfaga con "k<=n".
2. Escribir la inicialización, la cual debe asegurar que el invariante se cumpla antes de empezar a iterar.
3. Encontrar la condición de término. Esto se obtiene de comparar "qué le falta" al invariante para ser igual al estado final.
4. Escribir el cuerpo del ciclo, el cual debe:
- conseguir que el proceso avance, de modo que termine algún día, y
- preservar el invariante.
Estos dos últimos objetivos suelen ser contrapuestos. Al efectuar un avance en el proceso, los valores de las variables cambian, con el resultado que a menudo se deja de satisfacer el invariante. Por lo tanto, el resto del cuerpo del ciclo se suele dedicar a tratar de recuperar la validez del invariante.
2.1. Algoritmos: diagramas de flujo.
DEFINICIÓN
Un Algoritmo, se puede definir como una secuencia de instrucciones que representan un modelo de solución para determinado tipo de problemas. O bien, también como un conjunto de instrucciones que realizadas en orden conducen a obtener la solución de un problema. Por lo tanto podemos decir que es un conjunto ordenado y finito de pasos que nos permite solucionar un problema.
Los algoritmos son independientes de los lenguajes de programación. En cada problema el algoritmo puede escribirse y luego ejecutarse en un lenguaje de diferente programación.
PROGRAMA:
Un programa es una serie de instrucciones ordenadas,codificadas en lenguaje de programación que expresa un algoritmo y que puede ser ejecutado en un computador.
CLASIFICACIÓN DE ALGORITMOS
Los algoritmos se pueden clasificar en cuatro tipos:
Algoritmo computacional
Es un algoritmo que puede ser ejecutado en una computadora. Ejemplo: Fórmula aplicada para un cálculo de la raíz cuadrada de un valor x.
Algoritmo no computacional
Es un algoritmo que no requiere de una computadora para ser ejecutado. Ejemplo: Instalación de un equipo de sonido.

El algoritmo es la infraestructura de cualquier solución, escrita en cualquier lenguaje de programación.
- Debe ser Preciso, porque cada uno de sus pasos debe indicar de manera precisa e inequívoca que se debe hacer.
- Debe ser Finito, porque un algoritmo debe tener un número limitado de pasos.
- Debe ser Definido, porque debe producir los mismos resultados para las mismas condiciones de entrada.
- Puede tener cero o más elementos de entrada.
- Debe producir un resultado. Los datos de salida serán los resultados de efectuar las instrucciones
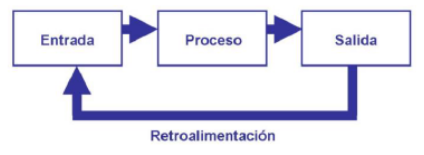
- Entrada de datos, son los datos necesarios que el algoritmo necesita para ser ejecutado.
- Proceso, es la secuencia de pasos para ejecutar el algoritmo.
- Salida de resultados, son los datos obtenidos después de la ejecución del algoritmo
- Diagramación libre (Diagramas de flujo).
- Diagramas Nassi-Shneiderman.
- Pseudocódigo.
- Lenguaje natural (español, inglés, etc.).
- Fórmulas matemáticas
Generalmente, se utilizan varios recuadros sencillos para los diagramas de flujo, los cuales buscan expresar etapas o procesos para conseguir un fin específico. La mayoría de las veces son utilizados para diagramas de ventas o ejemplificación del proceso de atención al cliente (en casos específicos).
Entre esos símbolos básicos de los diagramas de flujo destacan:
- Óvalos: Para iniciar o finalizar el diagrama de flujo.
- Rectángulos: Utilizados como cuadro de texto.
- Flechas: Representan la continuidad del diagrama. Funcionan como conectores entre símbolos y, de acuerdo a dónde apunte, indicarán la secuencia del proceso.
- Rombos: Sirven para identificar las preguntas o cuestionamientos dentro del proceso.
- Cuadrado: Desarrollo o proceso de control.
- Línea continua: Es el flujo de la información modo formulario o de documentación en apoyo de papel escrito.
- Línea interrumpida: Significa flujo de la información de modo de formulario digital.
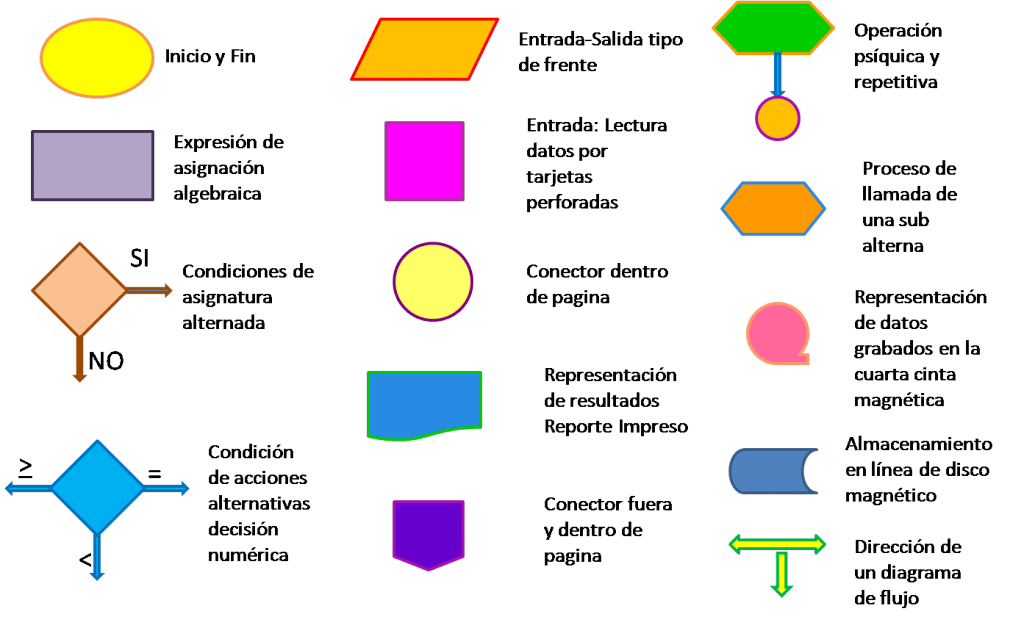
2.2. Diagramas de Flujo (SIMBOLOGÍA Y CONSTRUCCIÓN)
2.3. DIAGRAMA DE FLUJO - Ejercicio 1 - ANÁLISIS, CONSTRUCCIÓN Y PRUEBA DE ESCRITORIO