EL ALGEBRA EN SITUACIONES CONCRETAS DE LA REALIDAD.
5. Valor absoluto de una ecuación y una función lineal.
Funciones de valor absoluto
Una función de valor absoluto es una función que contiene una expresión algebraica dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un número es su distancia desde 0 en la recta numérica .
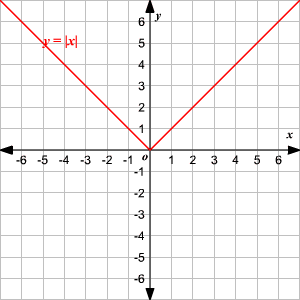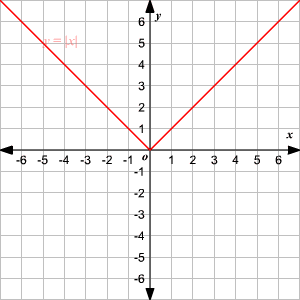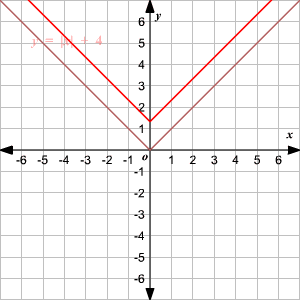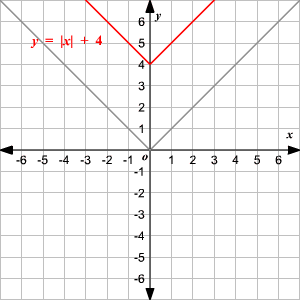
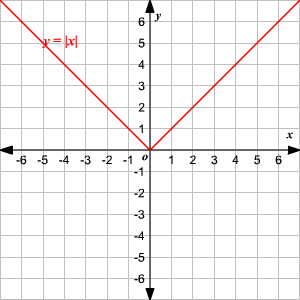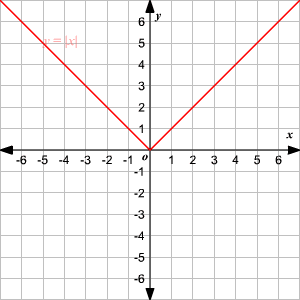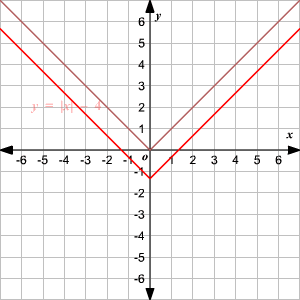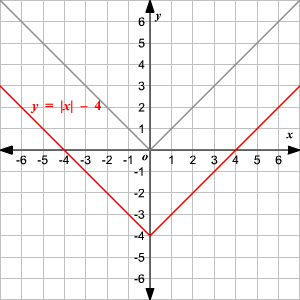
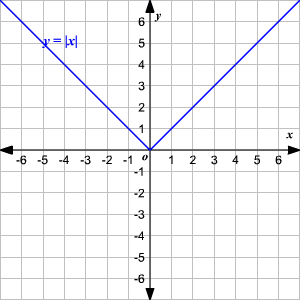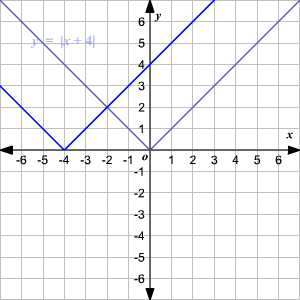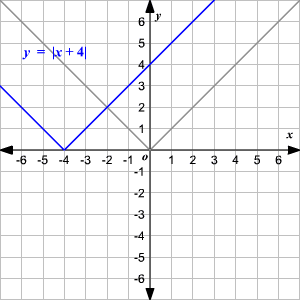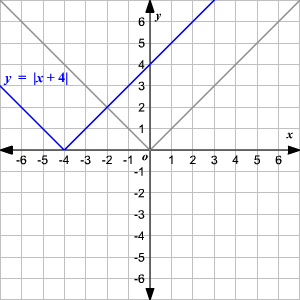
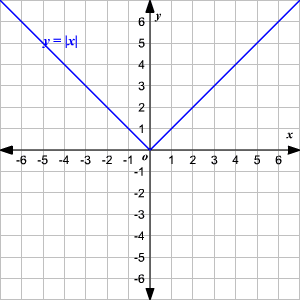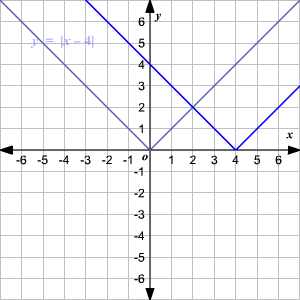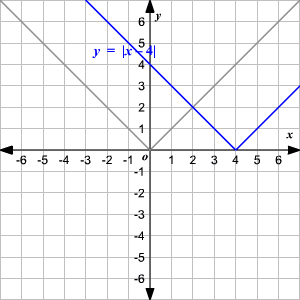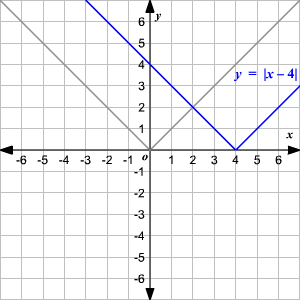
La función padre de valor absoluto, escrita como f ( x ) = | x |, está definida como
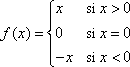
Para graficar una función de valor absoluto, escoja diferentes valores de x y encuentre algunas parejas ordenadas .
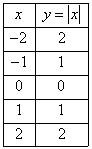
Grafique los puntos en una plano coordenado y unálos.
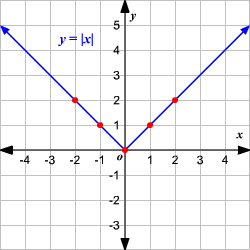
Observe que la gráfica es de la forma V. (1) El vértice de la gráfica es (0, 0). (2) El eje de simetria ( x = 0 o eje de las y ) es la recta que divide la gráfica en dos mitades congruentes. (3) El dominio es el conjunto de todos los números reales. 4) El rango es el conjunto de todos los números reales mayores que o iguales a 0. (5) La intercepción en x y la intercepción en y ambas son 0. Cambio Vertical Para trasladar la función valor absoluto f ( x ) = | x | verticalmente, puede utilizar la función g ( x ) = f ( x ) + k . Donde k > 0, la gráfica de g ( x ) se traslada k unidades hacia arriba. Donde k < 0, la gráfica de g ( x ) se traslada k unidades hacia abajo. Cambio Horizontal Para trasladar la función valor absoluto f ( x ) = | x | horizontalmente, puede utilizar la función g ( x ) = f ( x + k ). Donde k > 0, la gráfica de g ( x ) se traslada k unidades a la izquierda. Donde k < 0, la gráfica de g ( x ) translated k unidades a la derecha. .
.