EL ALGEBRA EN SITUACIONES CONCRETAS DE LA REALIDAD.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Matemáticas |
| Libro: | EL ALGEBRA EN SITUACIONES CONCRETAS DE LA REALIDAD. |
| Impreso por: | Invitado |
| Fecha: | jueves, 30 de enero de 2025, 23:44 |
1. Coordenadas rectangulares.
Sistema de coordenadas rectangulares
Dos líneas rectas perpendiculares entre sí, que se cortan, constituyen un sistema de ejes coordenados rectangulares.
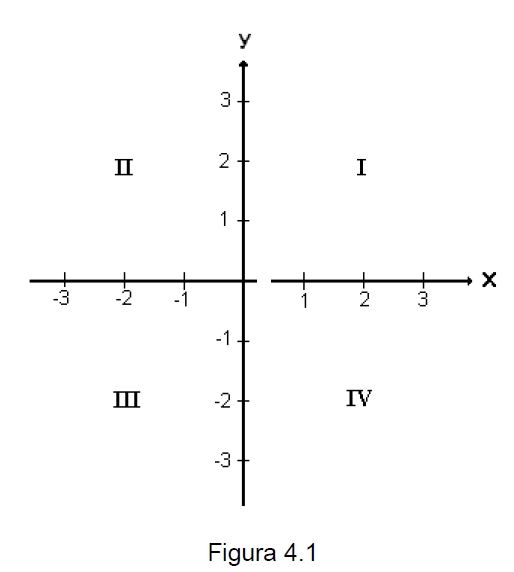
La recta horizontal de la figura 4.1 se llama eje x o eje de las abscisas, la recta vertical se llama eje y o eje de las ordenadas. El punto donde se cruzan los ejes se llama origen de coordenadas.
El sistema de coordenadas rectangulares también es llamado sistema de coordenadas cartesianas en honor al célebre matemático francés Rene Descartes, fundador de la geometría analítica.
Los ejes dividen al plano en cuatro partes llamadas cuadrantes, los números romanos de la figura anterior indican cuales son el primero (I), segundo (II), tercero (III) y cuarto cuadrante (IV).
Cada punto del plano está determinado por un par de números llamados coordenadas del punto en cuestión.
Ejemplo:
La figura 4.2a muestra cuatro puntos (en los diferentes cuadrantes) denotados con P1, P2 , P3 y P4 . En la figura 4.2b observarás que cada uno de los puntos anteriores se “conecta” a los ejes mediante líneas punteadas perpendiculares a los mismos, esas líneas nos llevan hasta la abscisa (o coordenada x) y la ordenada (o coordenada y) de cada punto.
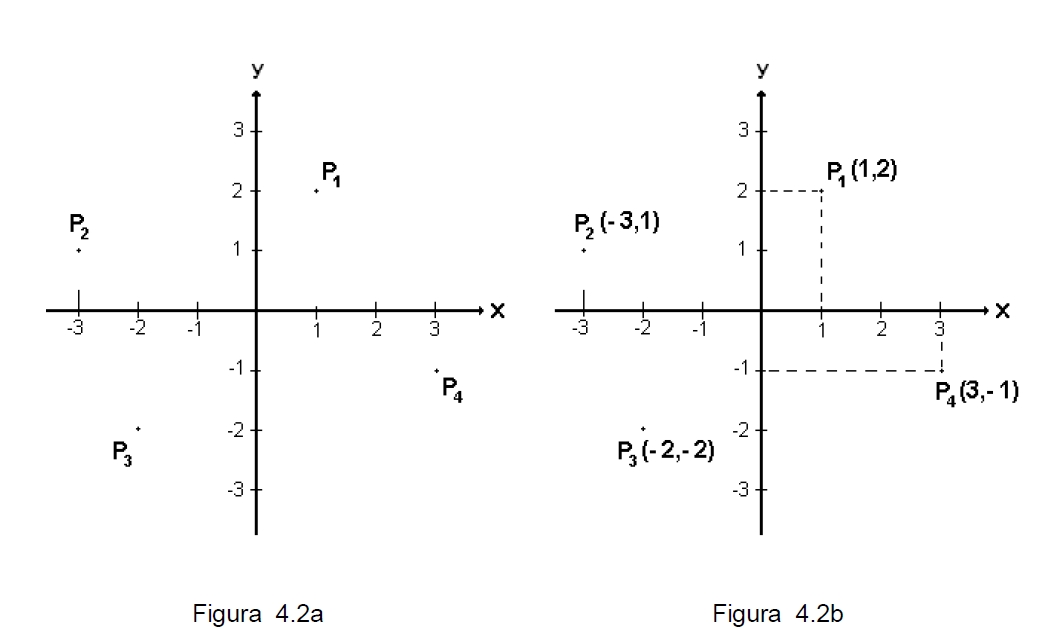
Así, el punto P1 tiene por coordenadas al par ordenado (1,2), el punto P2 tiene por coordenadas al par ordenado (-3,1), las coordenadas de P3 son (-2,-2) y las coordenadas de P4 son (3,-1).
En general, todo punto del plano tendrá coordenadas (x,y) y los signos de x y y dependerán del cuadrante en que se encuentre el pun to. A la pareja de números (x,y) se le llama par ordenado ya que x y yno pueden intercambiar posiciones (siguen un orden), porque si así lo hicieran representarían dos puntos diferentes.
Ejemplo:
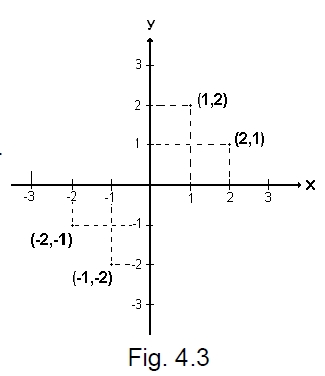
El punto (1,2) no es el mismo que el punto (2,1) como se muestra en la figura 4.3, de la misma manera el punto (-2,-1) no es el mismo que el punto (-1,-2). También los signos de las coordenadas son importantes, (2,1≠) (-2,-1).
Distancia entre dos puntos
Ela siguiente figura. Se quiere calcular la distancia entre los puntos P1 y P2 . Como podrás ver, los puntos P1 , P2 y P forman un triángulo rectángulo cuyos lados son:
La línea continua entre P1 y P2 , la línea a trazos entre P1 y P , y la línea a trazos entre P y P2.
La distancia entre los puntos P1 y P2 es la longitud de la hipotenusa del triángulo P1 P2 P. La longitud de la línea a trazos entre P1 y P se calcula tomando la diferencia de las ordenadas de los puntos P1 y P, mientras que la longitud de la línea a trazos entre P y P2 se calcula tomando la diferencia de las abscisas de los puntos P y P2.
Esto es, distancia P1 P = 3 –1 =2 , distancia P P2 = -1 – (-3) =2

Por lo tanto, aplicando el teorema de Pitágoras, la distancia P1 P2 está dada por:
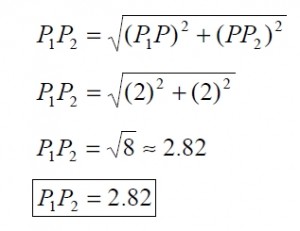
En general, la distancia “ d ” entre dos puntos del plano P( x2 , y2 ) y P1( x1 , y1 ) está dada por
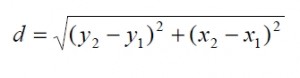
1.1. Producto cartesiano.
¿Qué es un producto cartesiano?
Se conoce como producto cartesiano al conjunto de todas las tuplas que se puedan obtener con los elementos de varios conjuntos. Una tupla es una secuencia ordenada de los elementos de un producto cartesiano o cualquier entidad matemática. Cuando una tupla esta formada sólo con dos elementos se le conoce como par ordenado ó dupla.
El producto cartesiano de dos conjuntos, es el conjunto de todos los pares ordenados que se pueden obtener con los elementos de dos conjuntos. Un par ordenado o una tupla de dos elementos, estará compuesto por un primer elemento de un conjunto y un segundo elemento de otro conjunto. Un par ordenado se escribe encerrando los elementos entre paréntesis y separados por una coma. Es decirdado dos conjuntos A y B, el producto cartesiano estará formado por los pares ordenados (a,b) en donde el primer elemento a pertenece al Conjunto A y el segundo elemento b pertenece al conjunto B. Expresado simbólicamente tenemos:
A x B = {(a,b)/ a ∈ A y b ∈ B}
En donde nos dice que el producto cartesiano de AxB, esta formado por los pares ordenados (a,b), tal que el primer elemento a pertenece al conjunto B y el segundo elemento b pertenece al conjunto B.
Ejemplo 1.Si A={3,4} y B={1,3,8} y C={3,8,9}, hallar (A x B) ⋂ (B x C).
Hallamos el producto cartesiano de AxB ={(3,1),(3,3),(3,8),(4,1),(4,3),(4,8)}
Hallamos el producto cartesiano de BxC={(1,3),(1,8),(1,9),(3,3),(3,8),(3,9),(8,3),(8,8),(8,9)}
Ahora hallamos la intersección de (A x B) ⋂ (B x C) = {(3,3),(3,8)}
La representación gráfica de un producto cartesiano se puede hacer con una tabla cartesiana, diagrama de flechas, diagrama cartesiano o un diagrama de árbol.
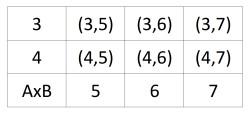
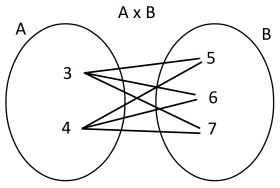
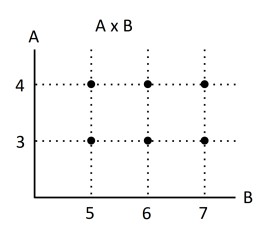
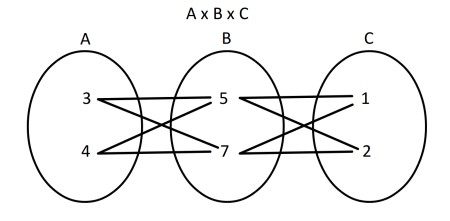
Ejemplo 2.Sea A={3,4} y B={5,6,7}, representar gráficamente el producto cartesiano de AxB, con una tabla cartesiana, un diagrama de flechas, diagrama cartesiano y un diagrama de árbol. Hallamos el producto cartesiano de A x B ={(3,5),(3,6),(3,7),(4,5),(4,6),(4,7)}
Tabla cartesiana:
Diagrama con flechas:
Diagrama cartesiano:
Para productos cartesianos de más de dos conjuntos, las tuplas estarán formadas por más de dos elementos, y en estos se suelen nombrar del siguiente modo. Para 3 elementos 3-tupla, tripla, tripleta, terna o triada, para 4 elementos 4-tupla o cuádrupla, para 5 elementos 5-tupla o quíntupla, para 6 elementos 6-tupla o sixtupla, para 7 elementos 7-tupla o septupla, para 8 elementos 8-tupla o octupla, para 9 elementos 9-tupla y asi sucesivamente.
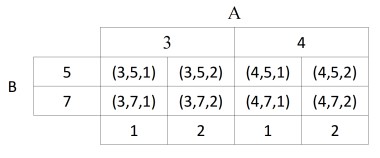
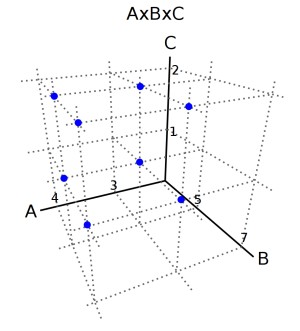
Ejemplo 3.Sea A={3,4}, B={5,7} y C={1,2} representar gráficamente el producto cartesiano de AxBxC, con una tabla cartesiana, un diagrama de flechas, diagrama cartesiano y un diagrama de árbol. Hallamos el producto cartesiano de AxBxC={(3,5,1)(3,5,2)(3,7,1)(3,7,2)(4,5,1)(4,5,2)(4,7,1)(4,7,1)}
Tabla cartesiana:
Diagrama con flechas:
Diagrama cartesiano (En perspectiva):
1.2. Pendiente de una recta en el plano cartesiano.
Pendiente de una recta
La pendiente m de una recta que pasa a través de dos puntos ( x 1 , y 1 ) y ( x 2 , y 2 ) es:
![]()
Si la gráfica de una recta sube de la izquierda a la derecha, la pendiente es positiva. Si la gráfica de la recta cae de la izquierda a la derecha la pendiente es negativa.
Ejemplo:
Encuentre la pendiente de la recta que pasa a través de los puntos (–3, 17) y (4, 3).
Sustituyendo x 1 = –3, y 1 = 17, x 2 = 4, y y 2 = 3, obtenemos:
![]()
Así la pendiente es –2.
Puede seguir los pasos siguientes para encontrar la pendiente de cualquier recta.
1) Escoja cualesquiera dos puntos en la recta. (Escoja puntos con coordenadas enteras para hacerse la vida más fácil.)
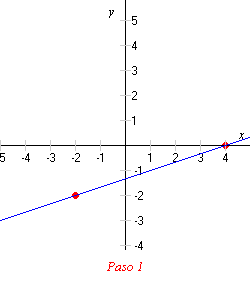
2) Dibuje una recta vertical que vaya hacia abajo desde el punto más alto.
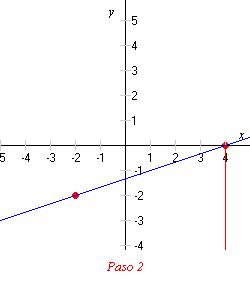
3) Dibuje una recta horizontal desde el otro punto para que así se encuentre con la recta vertical.
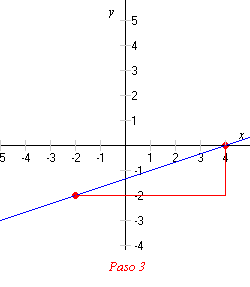
4) Ahora tiene un triángulo rectángulo, llamado un triángulo pendiente . Encuentre las longitudes de los catetos vertical y horizontal.
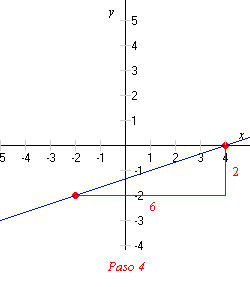
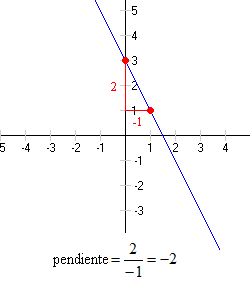
5) Divida la longitud del cateto vertical (la “subida”) entre la longitud del cateto horizontal (el “desplazamiento”). Este cociente es la pendiente de la recta.
![]()
Así la pendiente de la recta en este ejemplo es 1/3.
Si el ángulo recto está en el lado izquierdo del triángulo, la pendiente es negativa.
Rectas horizontales y verticales
Las rectas horizontales tienen pendiente cero, ya que la “subida” es cero.
Las rectas verticales tienen pendiente indefinida, ya que el “desplazamiento” es cero, y la división entre cero no está permitida.
PLANO CARTESIANO. Pendiente de una recta. Definición y Deducción de Fórmulas
1.3. Graficar la recta conociendo la pendiente y el punto de corte con el eje Y
2. Funciones lineales: Constante y Afín
Función constante, lineal y afínFunción constante
Es una función del tipo f (x) = k
Así, por ejemplo, si quisiésemos representar una cantidad que se mantiene constante a lo largo del tiempo t, utilizaríamos una función constante f(t) = k
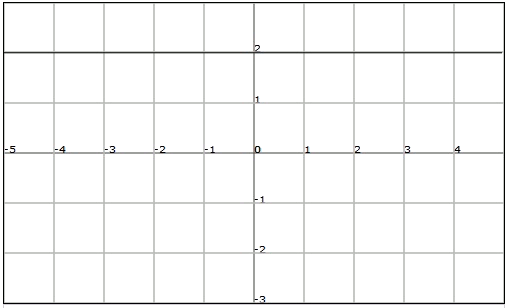
Las funciones constantes cortan el eje vertical en el valor de la constante y son paralelas al eje horizontal (y por tanto no lo cortan).
La gráfica de una función constante, por ejemplo f (x) = 2
Función lineal
La función de variable real que tiene por ecuación general y= mx
En las funciones lineales de este tipo (y = mx)

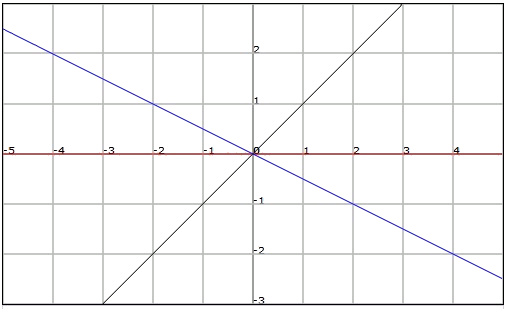
Es importante entender que como mayor es el valor del pendiente
Si m es positivo (m> 0
Si m es negativo (m <0
- Si m
El pendiente de una recta también puede ser calculado a partir de las coordenadas de un punto de la recta para una función lineal, y de las coordenadas de dos puntos en general para una recta cualquiera.
Veamos la manera general ya que nos servirá también para las funciones afines:
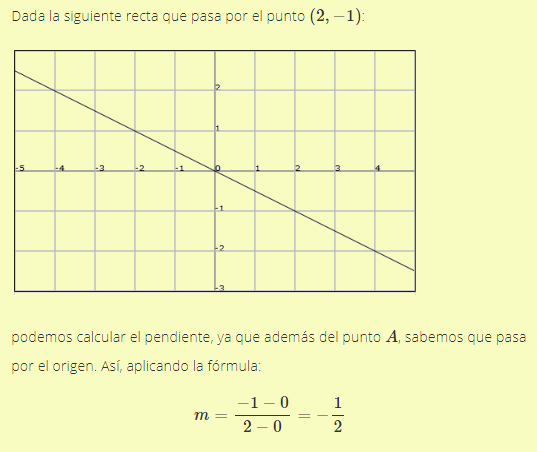
Dados dos puntos de una recta (sea una función lineal o afín), (x1, y1)
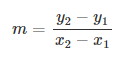
Ejemplo
Función afín
La función de variable real que tiene como ecuación general y = mx + n
Como en el caso anterior,
Es destacable también que el punto de corte de una función afín f(x) = mx + n con el eje de ordenadas es el punto (0, n).
Ejemplo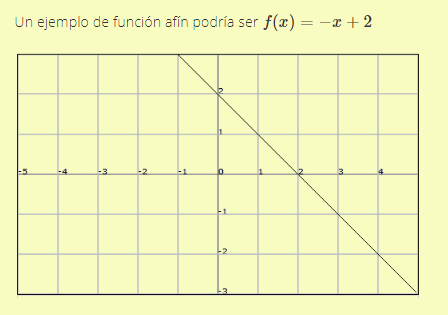
Funciones Lineales - De Proporcionalidad, Afines y Constantes
2.1. Funciones lineal, constante y afin
3. Ecuaciones lineales enteras y fraccionarias (1er grado de una incógnita
Una ecuación es una igualdad en la que hay una o varias cantidades desconocidas llamadas incógnitas.
Las incógnitas se representan por letras del alfabeto a, b, c, d, m, n, x, y, z. Asi;
![]()
En una ecuación se distinguen dos miembros, a saber; el primer miembro es la expresión que está a la izquierda del signo de igualdad (=) y el segundo miembro es la expresión que está a la derecha. Veamos

Ecuaciones de primer grado con una incógnita; son aquellas en las cuales el mayor exponente de la incógnita es uno, también se llaman ecuaciones simples o lineales. Estudiaremos las enteras y las fraccionarias. Ejemplos
![]()
Ecuaciones enteras de primer grado con una incógnita: cuando ninguno de sus términos tiene denominadores, así;
![]()
Ecuaciones fraccionarias de primer grado con una incógnita: cuando algunos de sus términos o todos tienen denominadores, como:
![]()
Solución de una ecuación de primer grado con una incógnita: es encontrar el valor de la incógnita que verifica o satisface la ecuación, es decir, que sustituido en lugar de la incógnita, hace que el lado izquierdo de la ecuación se iguale al lado derecho.
Para solucionar una ecuación de primer grado con una incógnita (hallar la raíz o el valor de la incógnita) se aplicará el proceso de transposición de términos, así:
- Reunir en un miembro todos los término que contengan la incógnita y en el otro miembro los demás términos.
- Cuando se pase un término de un miembro a otro se le cambia de signo: si el témino es positivo pasa al otro miembro negativo y si el término es negativo pasa al otro miembro positivo.
- Se reducen términos semejantes, si los hay.
- Si la incógnita tiene coeficientes se despeja: si está multiplicando pasa al otro miembro a dividir y si está dividiendo pasa al otro miembro a multiplicar (pasa con el signo que tenga).
- Si aparecen signos de agrupación, estos se eliminan primero (de adentro hacia afuera)
- Toda incógnita debe ser siempre positiva: si aparece negativa se le cambia el signo a todos los términos de la igualdad.
Ecuaciones de primer grado con una incognita ejemplos y ejercicios para resolver
3.1. Ecuaciones lineales de 1er grado con dos incógnitas
Un sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.
Ejemplo de un sistema:
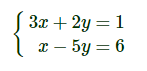
Es un sistema de dos ecuaciones con dos incógnitas (e .
Resolver un sistema de ecuaciones consiste en encontrar el valor de cada incógnita para que se cumplan todas las ecuaciones del sistema.
La solución al sistema del ejemplo anterior es
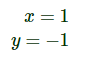
Pero no siempre existe solución, o bien, pueden existir infinitas soluciones. Si hay una única solución (un valor para cada incógnita, como en el ejemplo anterior) se dice que el sistema es compatible determinado. No hablaremos de los otros tipos ya que en esta página sólo se estudian los sistemas determinados. Para resolver un sistema (compatible determinado) necesitamos tener al menos tantas ecuaciones como incógnitas. En esta página resolvemos sistemas de dos ecuaciones (lineales) con dos incógnitas mediante los métodos que describimos a continuación, que se basan en la obtención de una ecuación de primer grado. Método de sustitución: consiste en despejar o aislar una de las incógnitas (por ejemplo, ) y sustituir su expresión en la otra ecuación. De este modo, obtendremos una ecuación de primer grado con la otra incógnita, . Una vez resuelta, calculamos el valor de sustituyendo el valor de que ya conocemos. Método de reducción: consiste en operar entre las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca. Así, obtenemos una ecuación con una sola incógnita. Método de igualación: consiste en aislar en ambas ecuaciones la misma incógnita para poder igualar las expresiones, obteniendo así una ecuación con una sola incógnita. No olvidemos que si multiplicamos una ecuación por un número distinto de 0, la ecuación inicial y la obtenida son equivalentes. Esto quiere decir que ambas ecuaciones tienen las mismas soluciones y, por tanto, podemos trabajar con una u otra. Usaremos esta propiedad con frecuencia en el método de reducción.
4. Inecuaciones lineales enteras y fraccionarias (1er grado de una incógnita)
Inecuaciones fraccionarias
Las inecuaciones fraccionarias o racionales tienen la incognita en el denominador.
Las inecuaciones racionales se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.
![]()
1º Hallamos las raíces del numerador y del denominador.
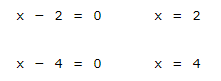
2º Representamos estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas.
3ºTomamos un punto de cada intervalo y evaluamos el signo en cada intervalo:
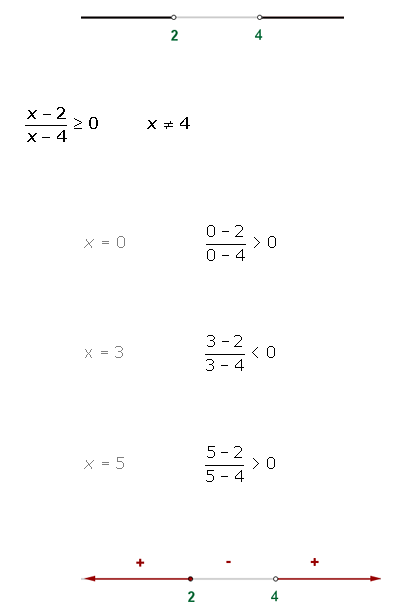
4º La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica.

Pasamos el 2 al primer miembro y ponemos a común denominador.
![]()
Hallamos las raíces del numerador y del denominador.
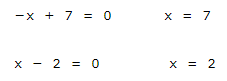
Evaluamos el signo:
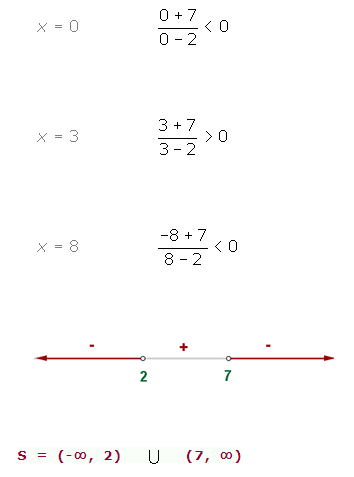
Ejercicios de inecuaciones fraccionarias
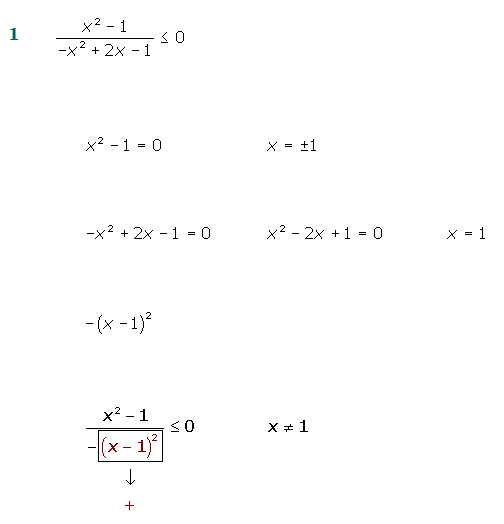
El binomio elevado al cuadrado es siempre positivo, pero al tener delante el signo menos. resultará que el demnominador será siempre negativo

Inecuaciones de Primer Grado - Lineales con fracciones| Ejemplo 1
5. Valor absoluto de una ecuación y una función lineal.
Funciones de valor absoluto
Una función de valor absoluto es una función que contiene una expresión algebraica dentro de los símbolos de valor absoluto. Recuerde que el valor absoluto de un número es su distancia desde 0 en la recta numérica .
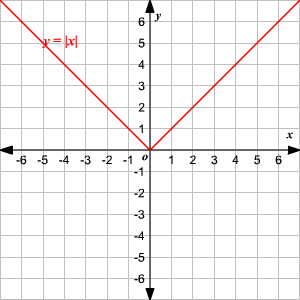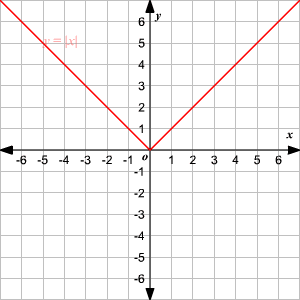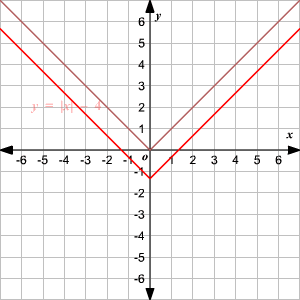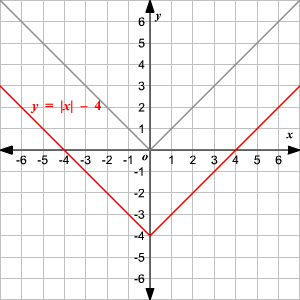
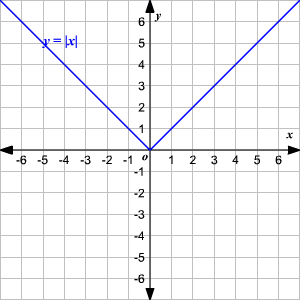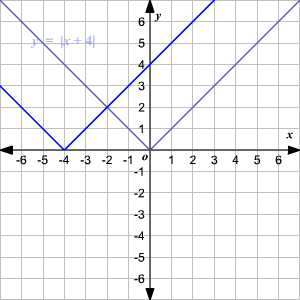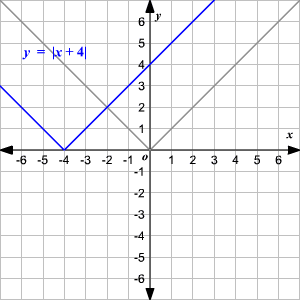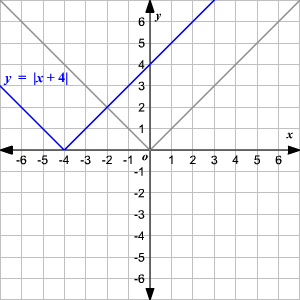
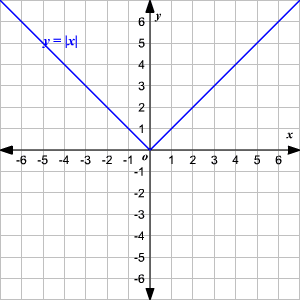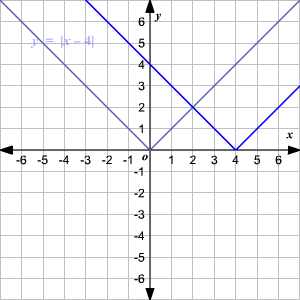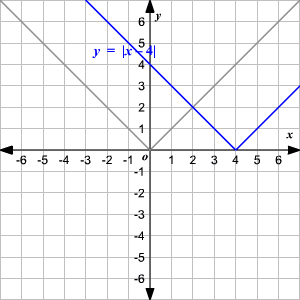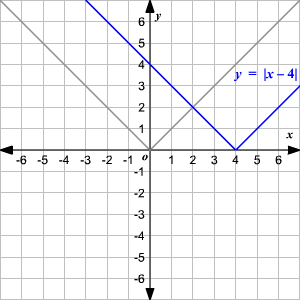
La función padre de valor absoluto, escrita como f ( x ) = | x |, está definida como
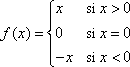
Para graficar una función de valor absoluto, escoja diferentes valores de x y encuentre algunas parejas ordenadas .
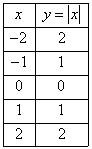
Grafique los puntos en una plano coordenado y unálos.
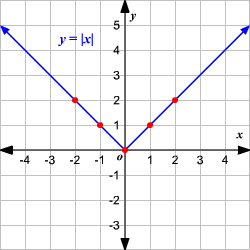
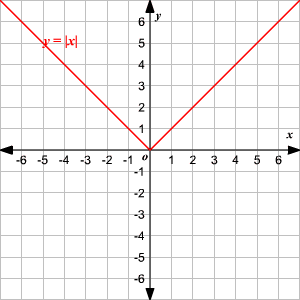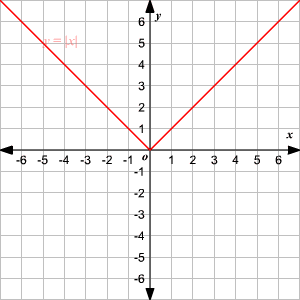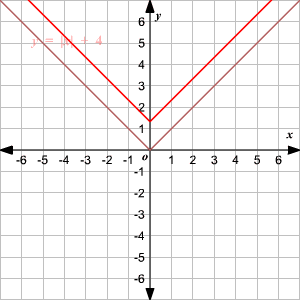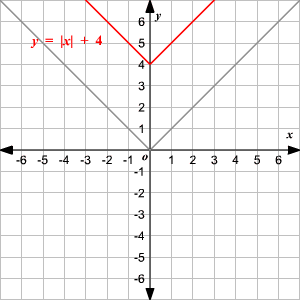
Observe que la gráfica es de la forma V. (1) El vértice de la gráfica es (0, 0). (2) El eje de simetria ( x = 0 o eje de las y ) es la recta que divide la gráfica en dos mitades congruentes. (3) El dominio es el conjunto de todos los números reales. 4) El rango es el conjunto de todos los números reales mayores que o iguales a 0. (5) La intercepción en x y la intercepción en y ambas son 0. Cambio Vertical Para trasladar la función valor absoluto f ( x ) = | x | verticalmente, puede utilizar la función g ( x ) = f ( x ) + k . Donde k > 0, la gráfica de g ( x ) se traslada k unidades hacia arriba. Donde k < 0, la gráfica de g ( x ) se traslada k unidades hacia abajo. Cambio Horizontal Para trasladar la función valor absoluto f ( x ) = | x | horizontalmente, puede utilizar la función g ( x ) = f ( x + k ). Donde k > 0, la gráfica de g ( x ) se traslada k unidades a la izquierda. Donde k < 0, la gráfica de g ( x ) translated k unidades a la derecha. .
.
5.1. Función Valor Absoluto - Ejercicios Resueltos - Nivel 1