EL ALGEBRA EN SITUACIONES CONCRETAS DE LA REALIDAD.
4. Inecuaciones lineales enteras y fraccionarias (1er grado de una incógnita)
Inecuaciones fraccionarias
Las inecuaciones fraccionarias o racionales tienen la incognita en el denominador.
Las inecuaciones racionales se resuelven de un modo similar a las de segundo grado, pero hay que tener presente que el denominador no puede ser cero.
![]()
1º Hallamos las raíces del numerador y del denominador.
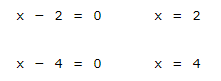
2º Representamos estos valores en la recta real, teniendo en cuenta que las raíces del denominador, independientemente del signo de la desigualdad, tienen que ser abiertas.
3ºTomamos un punto de cada intervalo y evaluamos el signo en cada intervalo:
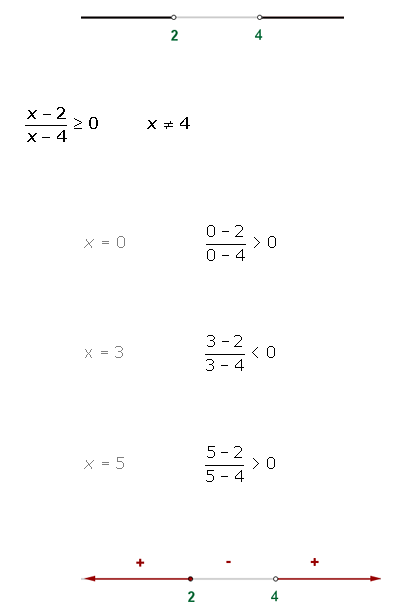
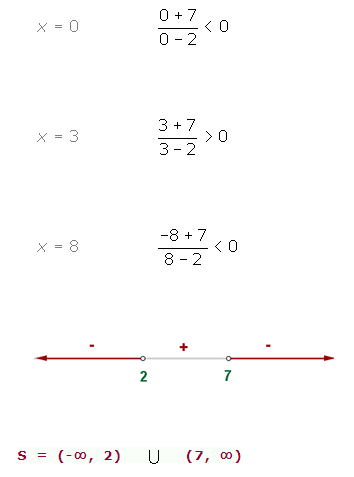
4º La solución está compuesta por los intervalos (o el intervalo) que tengan el mismo signo que la fracción polinómica.

Pasamos el 2 al primer miembro y ponemos a común denominador.
![]()
Hallamos las raíces del numerador y del denominador.
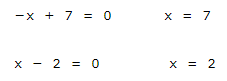
Evaluamos el signo:
Ejercicios de inecuaciones fraccionarias
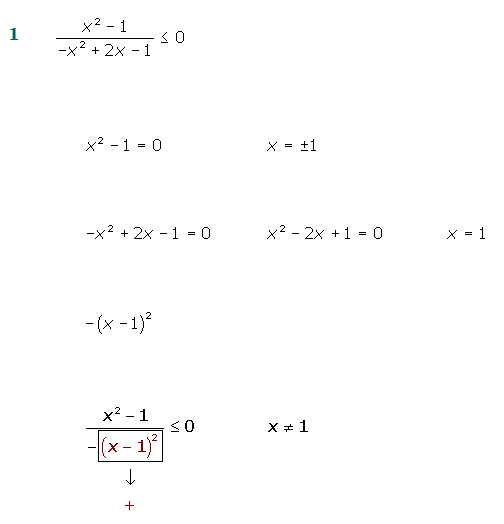
El binomio elevado al cuadrado es siempre positivo, pero al tener delante el signo menos. resultará que el demnominador será siempre negativo

Inecuaciones de Primer Grado - Lineales con fracciones| Ejemplo 1