EL ALGEBRA EN SITUACIONES CONCRETAS DE LA REALIDAD.

Es una función del tipo f (x) = k , donde k es un número real cualquiera. Fijémonos en que el valor de f (x) es siempre k, independientemente del valor de x.

Así, por ejemplo, si quisiésemos representar una cantidad que se mantiene constante a lo largo del tiempo t, utilizaríamos una función constante f(t) = k, en la que no aparece la variable t.

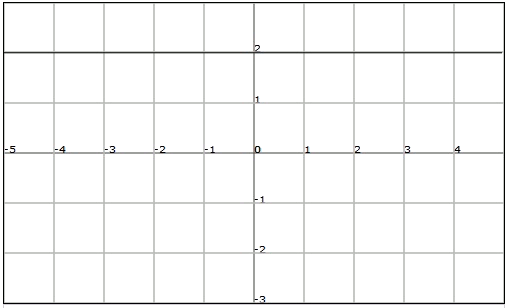
Las funciones constantes cortan el eje vertical en el valor de la constante y son paralelas al eje horizontal (y por tanto no lo cortan).

La gráfica de una función constante, por ejemplo f (x) = 2, es:

Función lineal

La función de variable real que tiene por ecuación general y= mx, cuya gráfica es una recta que pasa por el origen de coordenadas, se llama función lineal.

En las funciones lineales de este tipo (y = mx), el valor de m, que corresponde a un número real, se llama pendiente. El pendiente mide la inclinación de la recta respecto del eje de abscisas.

Es importante entender que como mayor es el valor del pendiente , mayor inclinación respecto el eje horizontal posee la recta. Además,

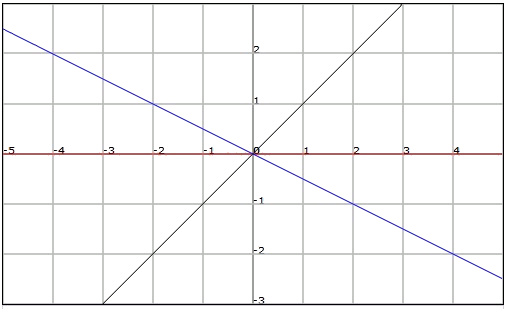
• Si m es positivo (m> 0), la recta pasa por el primer y por el tercer cuadrantes.

• Si m es negativo (m <0), la recta pasa por el segundo y cuarto cuadrantes.

• Si m es cero (m = 0), la recta es horizontal y coincide con el eje de abscisas.

El pendiente de una recta también puede ser calculado a partir de las coordenadas de un punto de la recta para una función lineal, y de las coordenadas de dos puntos en general para una recta cualquiera.

Veamos la manera general ya que nos servirá también para las funciones afines:

Dados dos puntos de una recta (sea una función lineal o afín), (x₁, y₁) y  (x₂,y₂), podemos calcular el pendiente de dicha recta mediante la expresión:

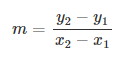
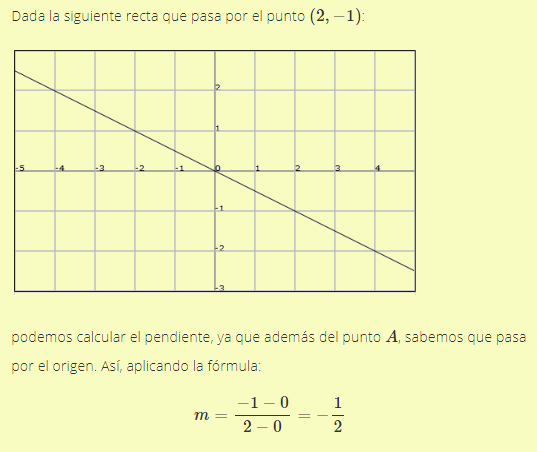
Ejemplo 

Función afín

La función de variable real que tiene como ecuación general y = mx + n , cuya gráfica es una recta que no pasa por el origen (si n\neq 0), se llama función afín.

Como en el caso anterior,  es el pendiente de la recta.

Es destacable también que el punto de corte de una función afín f(x) = mx + n con el eje de ordenadas es el punto (0, n).

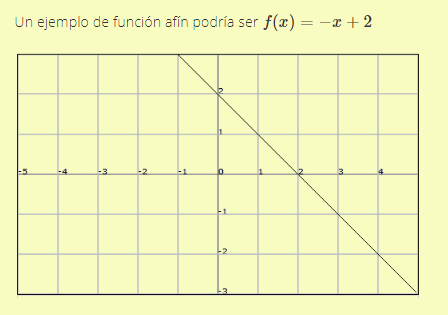
Funciones Lineales - De Proporcionalidad, Afines y Constantes