El Dibujo Tecnico en la Produccion

Curvas Geométricas

Se define a una línea como curva geométrica cuando se aparta constantemente de la dirección recta sin formar ángulos, y la trayectoria de los puntos que la forman es continua y, además, cumple una determinada norma. Existen dos grupos de curvas geométricas: las denominadas planas y las alabeadas. Una curva recibe el nombre de plana cuando todos sus puntos están situados en un mismo plano; y curva alabeada cuando cuatro de sus puntos no se encuentran en el mismo plano. Dependiendo de la forma que tengan de generarse, las curvas planas se dividen en curvas técnicas y curvas cónicas, que poseen propiedades específicas y distintas entre sí.

Curvas técnicas

Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico. Las curvas de este tipo se configuran mediante la unión de arcos de circunferencia que son tangentes entre sí, dando lugar a la formación de figuras planas que pueden ser cerradas: óvalo, ovoide; o abiertas: espirales, evolvente del círculo, etcétera.

A)     Óvalo

Es una curva plana y cerrada, simétrica respecto a sus dos ejes perpendiculares y formada por cuatro arcos de circunferencia iguales dos a dos.

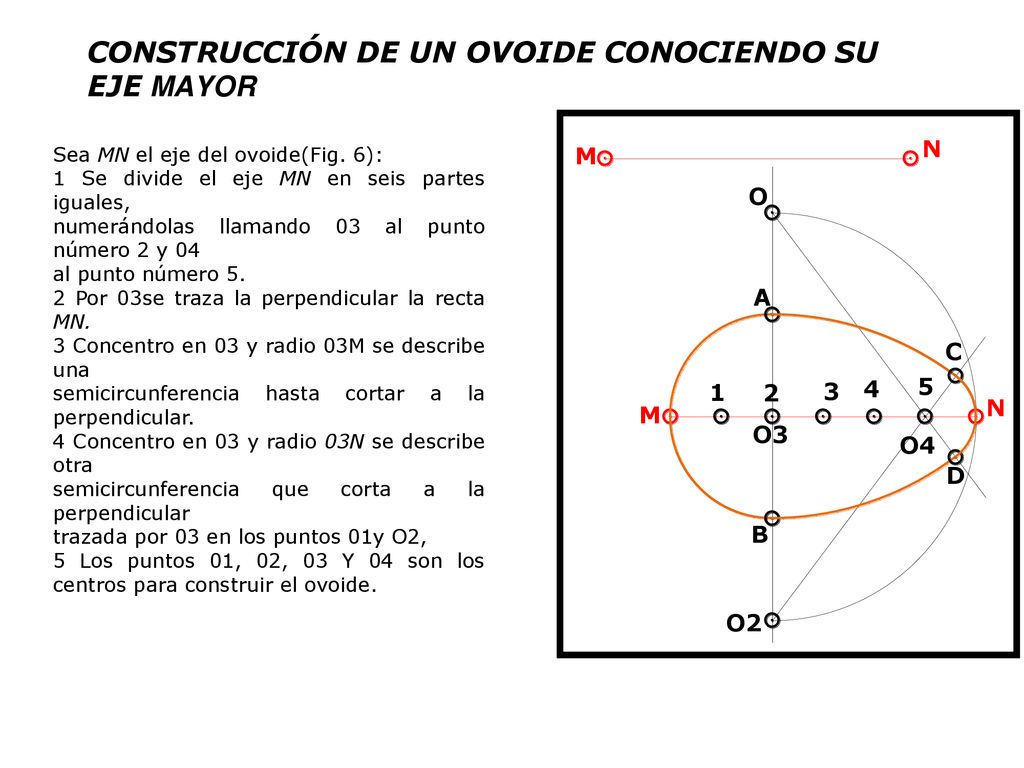
B)     Ovoide

El ovoide es una curva plana y cerrada, simétrica sólo respecto a su eje mayor, y formada por cuatro arcos de circunferencia, de los que dos son iguales y los otros dos son desiguales.

 

C)      Espiral

La espiral es una curva plana, abierta y continua que se configura en expansión por un punto que se desplaza de manera uniforme a lo largo de una recta, estando ésta fija en un punto por el cual gira con un valor angular constante. Una espiral se define por los siguientes elementos:

 

-          Paso: es la distancia longitudinal con que se desplaza un punto de la curva en una vuelta completa. Es decir, es la distancia entre dos espiras consecutivas.

-          Espira: es la parte de la curva descrita en cada vuelta.

-          Núcleo: es a partir de donde se genera, en expansión, la espiral. Los núcleos pueden ser lineales si los centros están situados en una línea, o poligonales si son los vértices del polígono los centros que generan la curva.

-          Radios vectores: son la prolongación, bien de la línea donde están situados los centros del núcleo, o bien de los lados del polígono que hace de núcleo.

 

D)      Voluta

Se denomina voluta a la curva plana, abierta y continua compuesta por arcos de circunferencia, tangentes entre sí, siendo los centros de los arcos los vértices de un polígono básicamente regular.

E)     Espiral de Arquímedes

Está generada por la trayectoria de un punto que se mueve de modo rectilíneo uniforme sobre una recta que gira a velocidad angular constante respecto a un punto fijo. Para definir el itinerario del punto se determina su situación en distintos momentos. Para ello, teniendo en cuenta que el punto se mueve con velocidad uniforme a lo largo de la semirecta y que la misma gira, respecto a su origen, con una velocidad angular constante, el punto en cuestión recorrerá segmentos iguales mientras la recta recorre ángulos iguales.