El Dibujo Tecnico en la Produccion
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Artes Plásticas y Visuales |
| Libro: | El Dibujo Tecnico en la Produccion |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 09:47 |
1. Curvas policéntricas: abiertas y cerradas
Curvas Geométricas
Se define a una línea como curva geométrica cuando se aparta constantemente de la dirección recta sin formar ángulos, y la trayectoria de los puntos que la forman es continua y, además, cumple una determinada norma. Existen dos grupos de curvas geométricas: las denominadas planas y las alabeadas. Una curva recibe el nombre de plana cuando todos sus puntos están situados en un mismo plano; y curva alabeada cuando cuatro de sus puntos no se encuentran en el mismo plano. Dependiendo de la forma que tengan de generarse, las curvas planas se dividen en curvas técnicas y curvas cónicas, que poseen propiedades específicas y distintas entre sí.
Curvas técnicas
Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico. Las curvas de este tipo se configuran mediante la unión de arcos de circunferencia que son tangentes entre sí, dando lugar a la formación de figuras planas que pueden ser cerradas: óvalo, ovoide; o abiertas: espirales, evolvente del círculo, etcétera.
A) Óvalo
Es una curva plana y cerrada, simétrica respecto a sus dos ejes perpendiculares y formada por cuatro arcos de circunferencia iguales dos a dos.

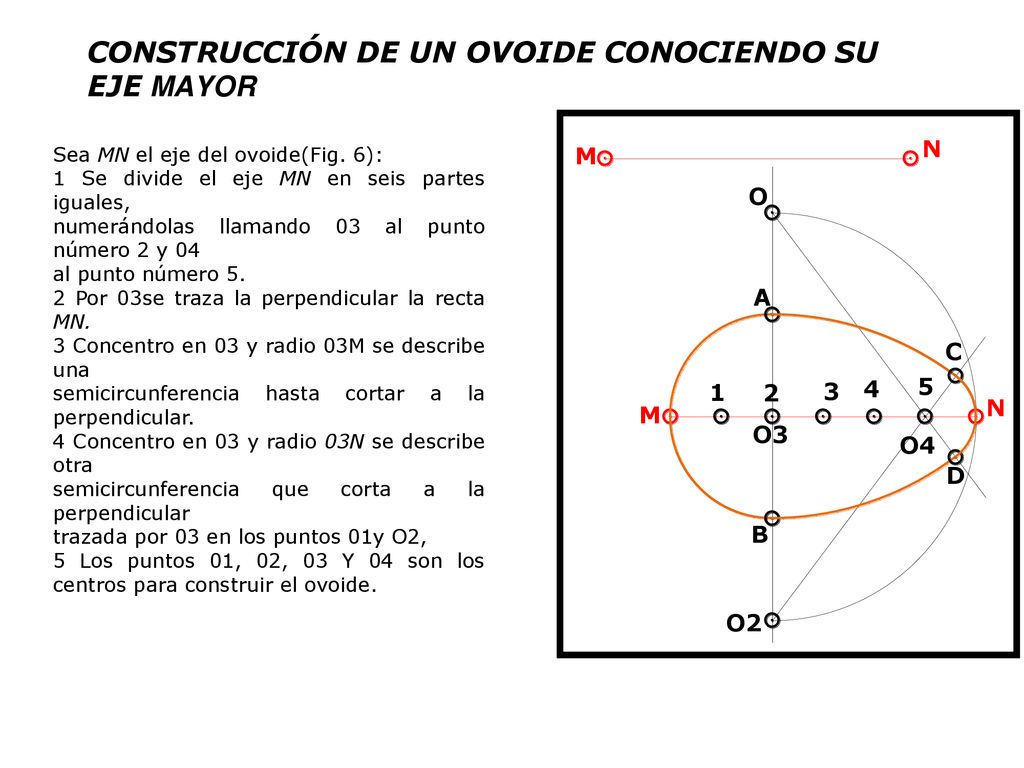
B) Ovoide
El ovoide es una curva plana y cerrada, simétrica sólo respecto a su eje mayor, y formada por cuatro arcos de circunferencia, de los que dos son iguales y los otros dos son desiguales.
C) Espiral
La espiral es una curva plana, abierta y continua que se configura en expansión por un punto que se desplaza de manera uniforme a lo largo de una recta, estando ésta fija en un punto por el cual gira con un valor angular constante. Una espiral se define por los siguientes elementos:
- Paso: es la distancia longitudinal con que se desplaza un punto de la curva en una vuelta completa. Es decir, es la distancia entre dos espiras consecutivas.
- Espira: es la parte de la curva descrita en cada vuelta.
- Núcleo: es a partir de donde se genera, en expansión, la espiral. Los núcleos pueden ser lineales si los centros están situados en una línea, o poligonales si son los vértices del polígono los centros que generan la curva.
- Radios vectores: son la prolongación, bien de la línea donde están situados los centros del núcleo, o bien de los lados del polígono que hace de núcleo.



D) Voluta
Se denomina voluta a la curva plana, abierta y continua compuesta por arcos de circunferencia, tangentes entre sí, siendo los centros de los arcos los vértices de un polígono básicamente regular.

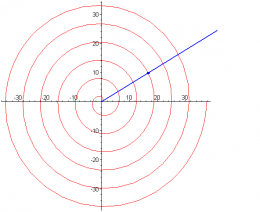
E) Espiral de Arquímedes
Está generada por la trayectoria de un punto que se mueve de modo rectilíneo uniforme sobre una recta que gira a velocidad angular constante respecto a un punto fijo. Para definir el itinerario del punto se determina su situación en distintos momentos. Para ello, teniendo en cuenta que el punto se mueve con velocidad uniforme a lo largo de la semirecta y que la misma gira, respecto a su origen, con una velocidad angular constante, el punto en cuestión recorrerá segmentos iguales mientras la recta recorre ángulos iguales.
2. Curvas cónicas: elipse, parábola e hipérbola aplicada a la tecnología
Las curvas cónicas se obtienen al seccionar un cono de revolución con un plano secante. Un cono de revolución es un cuerpo geométrico que puede considerarse engendrado por una línea recta denominada generatriz, que se mueve fija en un punto (centro de generación o vértice del cono) alrededor de un eje y con una dirección circular denominada directriz. La posición del plano secante respecto al eje del cono posibilita diferentes tipos de curvas. Además de la circunferencia, que se genera cuando el plano sección es perpendicular al eje del cono, son figuras cónicas la elipse, la parábola y la hipérbola.

Elementos de las curvas cónicas Veamos los elementos más importantes que componen las curvas cónicas y que son necesarios para su construcción:
• Focos: son los puntos de contacto de las esferas inscritas en el cono con el plano secante que genera las secciones cónicas, y están situados en el eje de simetría. La elipse y la hipérbola tienen dos focos, y la parábola tiene sólo uno.
• Vértices: son los puntos extremos de los ejes de la curva.
• Ejes: son los ejes de simetría de la curva. Tanto la elipse como la hipérbola tienen dos ejes de simetría que son perpendiculares entre sí. La parábola tiene solamente uno.
• Centro: es el punto donde se cortan los ejes de simetría y, por tanto, el centro de la curva.
• Directrices: son las rectas de intersección que realiza el plano secante, plano que genera la curva cónica, con los planos que contienen a las circunferencias tangentes de las esferas con el cono.
• Circunferencia principal: es el lugar geométrico de las proyecciones de los focos sobre las rectas tangentes a la cónica. El centro de esta circunferencia es el centro de la elipse o de la hipérbola y el radio es igual a la mitad de su eje mayor. En el caso de la parábola, el radio es infinito.
• Circunferencia focal: es el lugar geométrico de los puntos simétricos del otro foco respecto de las rectas tangentes a la cónica. En el caso de la elipse y la hipérbola, el centro de estas circunferencias son los focos y los radios son la longitud del eje mayor. En la parábola, el radio es infinito.
Elipse
Es una curva plana y cerrada, lugar geométrico de todos los puntos del plano cuya suma de distancias a dos puntos fijos, llamados focos, es constante e igual al eje mayor.
Elementos de la elipse Los elementos más significativos que configuran la elipse son los siguientes:
• Ejes: tiene dos ejes perpendiculares entre sí, que se cortan en el punto O, centro de la elipse. El eje mayor se denomina eje real o principal y el eje menor secundario o virtual. Esta curva es simétrica respecto a dichos ejes.
• Focos: están situados en el eje real y se hallan haciendo centro en uno de los extremos del eje virtual, con radio igual al semieje real.
• Distancia focal: es la distancia que existe entre los dos focos.
• Radios vectores: son las rectas que unen un punto cualquiera de la elipse con los focos.
• Circunferencia principal: es la que se determina haciendo centro en O, centro de la elipse, y con radio igual al semieje mayor.
• Circunferencia focal: la elipse tiene dos circunferencias focales. Para dibujarlas se toma como radio el eje real y centro, respectivamente.

Hipérbola
La hipérbola es una curva plana y abierta, lugar geométrico de todos los puntos del plano cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante e igual al eje real, es decir, a la distancia entre los vértices. Elementos de la hipérbola Los elementos más significativos que configuran la hipérbola son los que se indican a continuación:
• Ejes: la hipérbola tiene dos ejes, un eje imaginario, perpendiculares entre sí, que se cortan en el punto O. La hipérbola consta de dos ramas simétricas respecto de los dos ejes.
• En esta curva la distancia desde el centro de simetría O a cada foco es igual a la distancia AC, siendo A un extremo del eje real y C un extremo del eje imaginario. Esta propiedad permite, si se conoce uno de los ejes y los focos, determinar el otro eje, y, lógicamente, si se conocen los dos ejes, se pueden obtener los focos.
• Focos: están situados en el eje real y se hallan haciendo centro en O y radio igual a la distancia AC.
• Distancia focal: es la distancia que existe entre los dos focos.
• Radios vectores: son las rectas que unen un punto cualquiera de la hipérbola con los focos.
• Circunferencia principal: es la que se determina haciendo centro en O, centro de la hipérbola, y radio igual a la distancia AO del semieje real.
• Circunferencia focal: la hipérbola tiene dos circunferencias focales. Para dibujarlas se toma como radio el eje real y centro, respectivamente.
• Asíntotas: son rectas que pasan por el centro de la hipérbola y tangentes a ella en el infinito; además, son simétricas respecto de los ejes AB y CD.

Parábola
Una parábola es una curva plana y abierta, lugar geométrico de todos los puntos del plano equidistantes de uno fijo llamado foco F y de una recta d denominada directriz. Elementos de la parábola Los elementos más significativos que configuran la hipérbola son los que se indican a continuación:
• Eje: tiene sólo un eje de simetría, perpendicular a la directriz, y que contiene al vértice y al foco.
• Radios vectores: son las rectas que unen un punto cualquiera de la parábola con el foco.
• Circunferencia principal: tiene un radio infinito y es tangente a la parábola en su vértice.
• Circunferencia focal: también tiene un radio infinito y se convierte en una recta que coincide con la directriz.
• Parámetro: es la longitud de la cuerda de la parábola, perpendicular al eje, que pasa por el foco.
• Semi-parámetro: es la distancia desde el foco a la directriz.

3. Construcción de arcos
Se trata de hacer pasar un arco de circunferencia, o bien una circunferencia completa, por tres puntos (no alineados) que se tienen como datos.
OPERACIONES:
1. Se unen los tres puntos, dos a dos, por ejemplo, A-B y B-C.
2. Se trazan las mediatrices de los segmentos AB y BC.
3. El punto O, donde se cortan las dos mediatrices, es el centro del arco solicitado. Desde este punto se traza el arco o la circunferencia que deberá pasar por los tres puntos.

Determinar el centro de un arco de circunferencia
OPERACIONES:
1. Se toman tres puntos A, B y C cualesquiera a partir del arco dado.
2. Se unen los tres puntos, dos a dos, por ejemplo A-B y B-C.
3. Se trazan las mediatrices de los segmentos AB y BC. El centro del arco (O) está situado donde se cortan las mediatrices.

Trazado del Arco capaz
Se trata de determinar el arco capaz del ángulo a para el segmento dado.
OPERACIONES:
1. Se traza el segmento AB y se halla su mediatriz.
2. Sobre el segmento se construye el ángulo a.
3. En el punto A, se traza una perpendicular a r (lado del ángulo construido), corta a la mediatriz en O.
4. Haciendo centro en O (centro del arco capaz), se traza el arco que pase por A y B.


Construcción de un arco de gran radio
Se trata de construir un arco de gran radio conociendo la cuerda AB y la flecha CD.
OPERACIONES:
1. Por D (extremo de la flecha) se traza una paralela a la cuerda AB.
2. Por los extremos de la cuerda AB, se trazan perpendiculares a la misma.
3. Se une el punto D con A y B, y se levantan perpendiculares a DA y DB en los puntos A y B.
4. Se dividen los segmentos AC, CB, AE, BF, DM y DN en igual número de partes y se numeran.
5. Se une D con 1′, 2′, y 3′; y 3, 2 y 1 con 3”, 2” y 1”. La intersección de estos puntos da la mitad del arco.
6. Se realiza la misma operación en la otra mitad y se traza el arco por los puntos obtenidos.

4. Introducción a la perspectiva a partir de la naturaleza y los elementos socioculturales
¿Qué es la perspectiva?
En el ámbito del dibujo, perspectiva es la apariencia de tridimensión sobre una superficie. Hay dos grandes tendencias, la de utilizar paralelas para lograr tal representación y la de utilizar los llamados puntos de fuga. La perspectiva trata de recrear la profundidad. El problema central de la perspectiva es representar la apariencia de profundidad coherentemente. Las decenas de métodos existentes son hipótesis que pretenden solucionar desde distintos procedimientos tal problema.

Perspectiva Axonométrica
La axonometría es la parte de la geometría descriptiva que se encarga de representar objetos en las proyecciones de tres ejes. Por axonometría se debe entender el dibujo mediante ejes (axe = ejes). Los ejes son X, Y y Z, que significan la longitud (X). la altura (Y) y la profundidad (Z), de acuerdo al plano cartesiano.

Perspectiva Caballera
Al emplearse medidas y trazos en los tres ejes, la caballera, como las dimétricas y trimétricas respectivamente así como la isométrica, son axonométricas. En la perspectiva cabellera se presenta una imagen totalmente de frente y se proyecta en ángulo la profundidad. Generalmente los ángulos utilizados son los de las escuadras, 45º, 30º y 60º. Se utiliza más para cuestiones técnicas, que para dibujos más artísticos. Se tienen que usar factores de reducción para contemplar una escena realista, para 30º se usa 2/3 como factor de reducción; para 45º se usa 1/2 como factor de reducción, para 60º se usa 1/3. El factor de reducción se usa exclusivamente sobre el eje Z, la profundidad.

Perspectiva Isométrica
Viene se isos = igual y metros = medida. Esto es medidas iguales en los ejes. Dados los tres ejes de referencia, el dibujo se representa con medidas reales (aunque casi siempre a escala). Las medidas en diagonales no son isométricas, en el sentido horizontal la medida es mayor y en el vertical es menor. Se utiliza fundamentalmente al cartabón ya que los ángulos básicos son 30º a partir de la horizontal. La proporción a escala se representa 1:1, se lee uno es a uno, quiere decir que un elemento real es igual al elemento representado, no hay factor de corrección en ninguno de los tres ejes. Como en el dimétrico y el trimétrico. En la ilustración debajo, 1 es dimétrico, se dibuja a 7º, 90º y 42º, usa dos medidas, en el lado corto se usó como factor de reducción ½. El trimétrico, (dibujo 2) usa tres factores de medidas y dos factores de reducción, sólo la altura es tal cual. Los factores son ½ y 9/10, los ángulos que utiliza son 5º, 18º y 90º Es muy útil por la sencillez de su técnica y rápido aprendizaje, se venden inclusive papeles isométricos que facilitan la labor de dibujo a mano alzada a escala fácil y pronta.

Perspectiva cónica
La clave de la perspectiva cónica es que lo lejano se percibe más pequeño que lo cercano, por eso el dimétrico y trimétrico usan factores de reducción. Las muy diferentes técnicas para dibujar en perspectiva basan sus divergencias en el cómo hacer que los objetos se vean más pequeños, sin deformaciones aparentes. La palabra latina perspectiva deriva de perspicere (ver claramente) y corresponde al griego skele (ciencia de la visión), dibujar en perspectiva es ser perspicaz, es mirar con ciencia, con certeza. Si un objeto (o partes de él) se ve empequeñecido por la distancia, se necesita un factor de reducción, que permita la apariencia realista de lo representado.

Elementos de la perspectiva
Toda perspectiva tiene elementos en común, independientemente de la técnica utilizada para el cálculo de la disminución de tamaño por la distancia. Estos elementos en común son:
§ Línea de tierra
§ Línea de horizonte
§ Punto de fuga
§ Módulos horizontales
§ Módulos verticales
§ Posición aparente del observador
§ Altura aparente del observador
Línea de tierra
Nivel desde el que parten las modulaciones horizontales y verticales. Es la parte baja del campo de visión. El límite de lo que se ve en la perspectiva.
Línea de horizonte
Corresponde a la línea imaginaria en donde se posa la vista, el horizonte. Sobre esta línea horizontal se encuentran los diversos puntos de fuga. Puede haber 1, 2, 3…n cantidad de puntos de fuga.
Punto de fuga
Es el lugar al que aparentemente se dirigen las líneas paralelas, al prolongarlas lo suficiente. El ejemplo típico es la imagen de un par de vías de ferrocarril, que parecen juntarse en un punto en el horizonte, aunque se sepa que siempre conservan la misma distancia. El punto de fuga siempre va sobre la línea de horizonte. Tomás García Salgado en su libro Perspectiva modular (1983) a diferencia de otros autores afirma que solo hay un punto de fuga, todos los demás son puntos auxiliares al punto de fuga principal.
Módulos horizontales y verticales
La modulación horizontal es la modulación de altura y anchura a escala, se tendrá sobre una línea horizontal y vertical unidades iguales, módulos, que a escala nos ayudarán a determinar tamaños. La modulación de profundidad consiste en dar una correcta modulación de lo que se aleja. Se presentará más adelante un método sencillo para calcular la disminución de tamaño con la distancia.
Módulos verticales
Los módulos verticales son la altura aparente de los objetos. En el límite visual de la perspectiva hay que situar las marcas de los módulos, tanto horizontales como verticales, determinar también la línea de horizonte. Es importante mencionar que se habla de módulos. Las medidas que tienen los módulos pueden ser cualesquiera, pero iguales, por ejemplo cada 3 centímetros.
Los módulos horizontales, verticales y de profundidad, pueden tener diferentes escalas, en una perspectiva, el módulo puede equivaler 1 metro, en otra perspectiva 10 metros. De esta manera se pueden crear perspectivas interiores o exteriores, de cuartos o edificios enteros. Se puede trabajar también a 1 punto de fuga central o usando los puntos de fuga auxiliares para tener dos o más puntos de fuga. Este método es una simplificación de los conceptos de García Salgado (1983).
Posición aparente del observador
Sitio virtual en que se encuentra el observador y que determina el cómo ver a los objetos en la perspectiva. El observador es quien aparentemente ve a los objetos situados dentro de los límites del campo de la perspectiva, su posición determina lo que se ve en la imagen. En la misma posición aparente la imagen se ve muy cerca, o lejana. El observador se acerca a lo representado o se aleja. Situar adecuadamente al espectador es importante. Ya que permite un dibujo que ilustre pertinentemente las ideas.
Altura aparente del observador
Situación similar ocurre cuando el espectador sube o baja su nivel de observación. Imaginar si se está en el elevador de un edificio. Se ve la misma imagen, pero desde arriba o abajo. Cuando sube el observador, sube también la línea de horizonte, cuando baja el observador. Baja el horizonte. La perspectiva está a nivel, si la línea de visión está a la misma altura que la línea de horizonte. La perspectiva está a ojo de hormiga, o contrapicada, si el nivel de horizonte está muy bajo, como si la perspectiva fuera vista por una hormiga. La perspectiva puede ser contemplada aún como desde un agujero. La perspectiva en picada o a vuelo de pájaro es cuando el observador está tan alto como desde un avión en vuelo, como si fuera la imagen contemplada por un pájaro. A esta última también se le puede llamar perspectiva aérea.