EL NÚMERO, LA FORMA Y EL CÁLCULO EN LA SOLUCIÓN DE PROBLEMAS O SITUACIONES DE CONTEXTO.
3. Los números reales (ℝ) y su Relación de orden.
3.1. Operaciones con los números reales R: Adición, sustracción, multiplicación y división aplicada a la producción en general.
Suma de números reales
Propiedades
1.Interna:
El resultado de sumar dos números reales es otro número real.
∀ a, b ∈ R : a + b ∈ R
2.Asociativa:
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c) ·
![]()
3.Conmutativa:
El orden de los sumandos no varía la suma.
a + b = b + a
![]()
4.Elemento neutro:
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
∀ a ∈ R, 0 + a = a + 0 = a
5.Elemento opuesto
Dos números son opuestos si al sumarlos obtenemos como resultado el cero.
e − e = 0
El opuesto del opuesto de un número es igual al mismo número.
a + ( -a) = -a + a = 0 , ∀ a ∈ R
La diferencia de dos números reales se define como la suma del minuendo más el opuesto del sustraendo.
a - b = a + (- b)
Multiplicación números realesLa regla de los signos del producto de los números enteros y racionales se sigue manteniendo con los números reales.
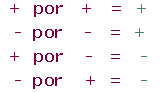
Propiedades
1.Interna:
El resultado de multiplicar dos números reales es otro número real.
∀ a, b ∈ R→ a • b ∈ R
2.Asociativa:
El modo de agrupar los factores no varía el resultado. Si a, b y c son números reales cualesquiera, se cumple que:
Si a, b, c, ∈ R → (a • b) • c = a • (b • c)
3.Conmutativa:
El orden de los factores no varía el producto.
a · b = b · a
![]()
El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.
a ·1 = a
5. Elemento inverso:
Un número es inverso del otro si al multiplicarlos obtenemos como resultado el elemento unidad.
![]()
![]()
6.Distributiva:
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
a · (b + c) = a · b + a · c
7.Sacar factor común:
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c)
La división de dos números reales se define como el producto del dividendo por el inverso del divisor.