EL NÚMERO, LA FORMA Y EL CÁLCULO EN LA SOLUCIÓN DE PROBLEMAS O SITUACIONES DE CONTEXTO.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 2° - Matemáticas |
| Libro: | EL NÚMERO, LA FORMA Y EL CÁLCULO EN LA SOLUCIÓN DE PROBLEMAS O SITUACIONES DE CONTEXTO. |
| Impreso por: | Invitado |
| Fecha: | viernes, 4 de abril de 2025, 08:51 |
1. Números racionales (ℚ).
Un número racional es todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por .
.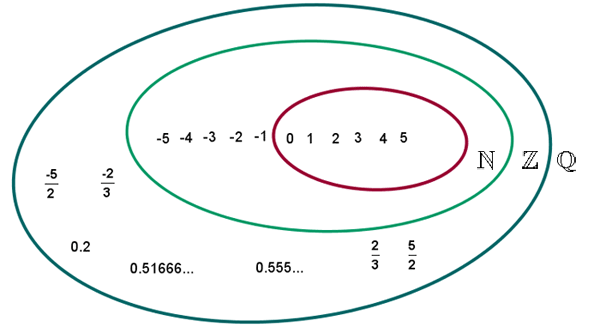
Representación de números racionales
Los números racionales se representan en la recta junto a los números enteros.
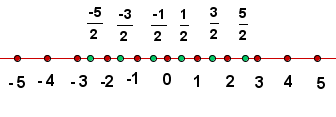
Para representar con precisión los números racionales:
1 Tomamos un segmento de longitud la unidad, por ejemplo.
2 Trazamos un segmento auxiliar desde el origen y lo dividimos en las partes que deseemos. En nuestro ejemplo, lo dividimos en 4 partes.
3 Unimos el último punto del segmento auxiliar con el extremo del otro segmento y trazamos segmentos paralelos en cada uno de los puntos, obtenidos en la partición del segmento auxiliar.
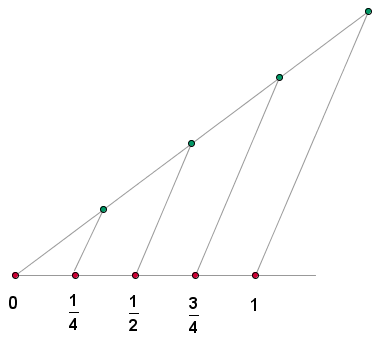
En la práctica se utilizan número racional y fracción como sinónimos.
1.1. Introducción a los números racionales | fracciones positivas o negativas
1.2. Operaciones en Q: Adición, sustracción, multiplicación y división aplicada al diario vivir.
Suma y resta de números racionales
Con el mismo denominador
Se suman o se restan los numeradores y se mantiene el denominador.
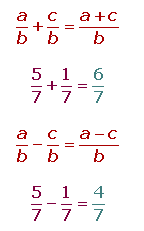
Con distinto denominador
En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
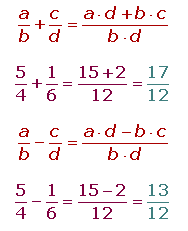
Propiedades de la suma de números racionales
1. Interna:
a + b ![]()
![]()
2. Asociativa:
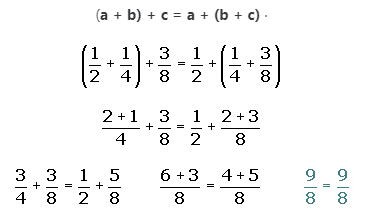
3. Conmutativa:
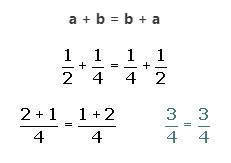
4. Elemento neutro:
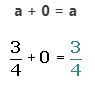
5. Elemento opuesto
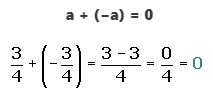
El opuesto del opuesto de un número es igual al mismo número.
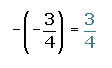
Multiplicación de números racionales
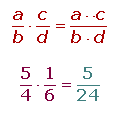
Propiedades de la multiplicación de números racionales
1. Interna:
a · b ![]()
![]()
2. Asociativa:
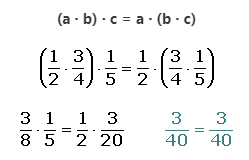
3. Conmutativa:
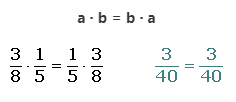
4. Elemento neutro:
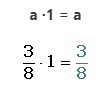
5. Elemento inverso:
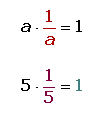
6. Distributiva:
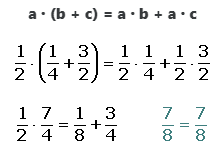
7. Sacar factor común:
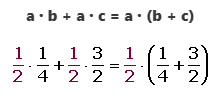
División de números racionales
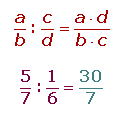
1.3. Operaciones en Q: Potenciación, radicación y sus propiedades.
Potencias de números racionales
Potencias de exponente entero y base racional
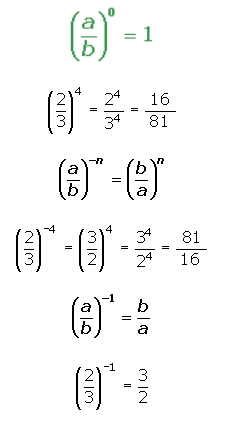
Propiedades
1.
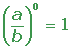
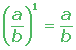
3. Producto de potencias con la misma base:
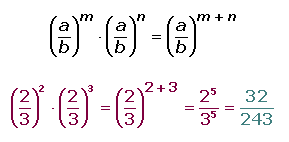
4. División de potencias con la misma base:
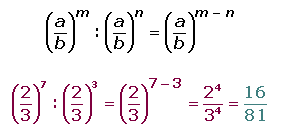
5. Potencia de una potencia:
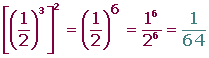
6. Producto de potencias con el mismo exponente:
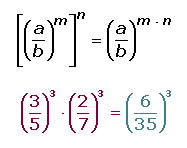
7. Cociente de potencias con el mismo exponente:
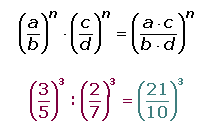
2. Los Números irracionales y su clasificación.
Número irracional
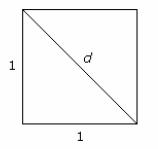
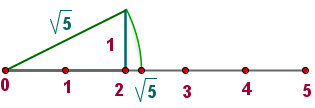
Los números irracionales surgen por la imposibilidad de resolver en Q ciertos problemas. Por ejemplo, si se quiere calcular la longitud de la diagonal de un cuadrado de lado 1, esto no es posible hacerlo en el conjunto de los números racionales, ya que por el Teorema de Pitágoras, llamando d a la longitud buscada, se ha de cumplir que:
El conjunto de los números irracionales se representa por I y está formado por todos los números decimales cuya parte decimal tienen infinitas cifras periódicas, es decir, por todos los números que no se pueden representar por el cociente de dos números enteros. Es inmediato que no existe ningún número que sea racional e irracional, es decir, Q C I =Ø
d2 = 12 + 12 = √2, de donde, d = √2 que no es un números racionales puesto que no se puede expresar como una fracción, en otras palabras, la expresión decimal √2 tiene infinitas cifras decimales.
Dentro de la recta real numérica existen varios conjuntos de números, pero dentro de los números irracionales hay más tipos para clasificar, estos son:
Número algebraico.- se les llama así a los números irracionales que surgen de resolver alguna ecuación algebraica y se escribe con un número finito de radicales libres o anidados. En general, las raíces no exactas de cualquier orden se encuentran dentro de este conjunto, es decir las raíces cuadradas, cúbicas, etc.
Número trascendente.- este es un número irracional que no puede ser representado a través de un número finito de radicales libres o anidados, estos provienen de otro tipo de operaciones llamadas funciones trascendentes utilizadas mucho en trigonometría, logaritmos, exponenciales, etcétera. Aunque también pueden surgir de la simple acción de escribir números decimales al azar sin periodicidad y sin un patrón determinado, podemos decir que son decimales infinitos.
Este último tipo, se diferencia del anterior porque no puede ser el resultado de una ecuación algebraica, en otras palabras, son relevantes a la clasificación porque no tienen una representación con un número radical.
Números irracionales famosos
Como se mencionaba anteriormente, existen números irracionales determinados que son utilizados en diferentes ramas, para operaciones específicas, algunos de ellos son:
Pi, o como se lo conoce mejor con su símbolo π, este es el más conocido de los números irracionales, y se utiliza en su mayoría para matemáticas, física e ingeniería. Su valor es el cociente entre la longitud o perímetro de la circunferencia y la longitud de su diámetro. De él se han calculado millones de cifras decimales y aún sigue sin ofrecer un patrón. La aproximación de su número es 3.141592653589…
e es otro número irracional famoso, utilizado en cálculo más que nada, es llamado también número de Euler, y de él también se han calculado infinidad de decimales sin llegar a encontrar una repetición periódica. Sus primeros decimales son 2,718281828459…
El número áureo o razón de oro, representado con la letra griega ϕ o phi también es muy utilizado por muchos artistas, en especial se lo conoce por las proporciones corporales usadas por Leonardo da Vinci, cuya aproximación es 1,618033988749…
2.1. Matemática - Números Irracionales
3. Los números reales (ℝ) y su Relación de orden.
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por  .
.
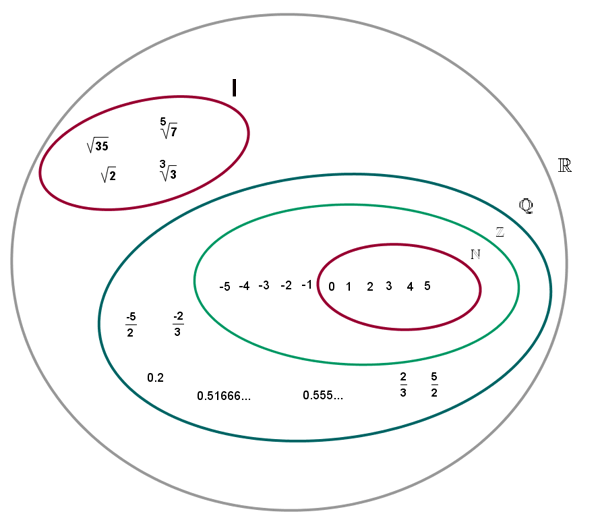
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
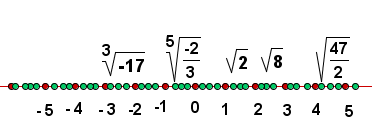
La recta real
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
![]()
3.1. Operaciones con los números reales R: Adición, sustracción, multiplicación y división aplicada a la producción en general.
Suma de números reales
Propiedades
1.Interna:
El resultado de sumar dos números reales es otro número real.
∀ a, b ∈ R : a + b ∈ R
2.Asociativa:
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c) ·
![]()
3.Conmutativa:
El orden de los sumandos no varía la suma.
a + b = b + a
![]()
4.Elemento neutro:
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
∀ a ∈ R, 0 + a = a + 0 = a
5.Elemento opuesto
Dos números son opuestos si al sumarlos obtenemos como resultado el cero.
e − e = 0
El opuesto del opuesto de un número es igual al mismo número.
a + ( -a) = -a + a = 0 , ∀ a ∈ R
La diferencia de dos números reales se define como la suma del minuendo más el opuesto del sustraendo.
a - b = a + (- b)
Multiplicación números realesLa regla de los signos del producto de los números enteros y racionales se sigue manteniendo con los números reales.
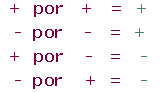
Propiedades
1.Interna:
El resultado de multiplicar dos números reales es otro número real.
∀ a, b ∈ R→ a • b ∈ R
2.Asociativa:
El modo de agrupar los factores no varía el resultado. Si a, b y c son números reales cualesquiera, se cumple que:
Si a, b, c, ∈ R → (a • b) • c = a • (b • c)
3.Conmutativa:
El orden de los factores no varía el producto.
a · b = b · a
![]()
El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.
a ·1 = a
5. Elemento inverso:
Un número es inverso del otro si al multiplicarlos obtenemos como resultado el elemento unidad.
![]()
![]()
6.Distributiva:
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
a · (b + c) = a · b + a · c
7.Sacar factor común:
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c)
La división de dos números reales se define como el producto del dividendo por el inverso del divisor.
3.2. Operaciones en (ℝ): Potenciación, radicación y sus propiedades.
Potenciación
Multiplicar un número b por sí mismo varias veces, puede indicarse como bn ,
que es lo mismo que multiplicar b, n veces: bn = b.b.b ....b
El número b se llama “base” y el n se llama “exponente” y decimos que bn es la
n-esima potencia de b.
Reglas de los exponentes
Producto de potencias de igual base
Para multiplicar dos o más potencias que tienen la misma base basta con sumar los exponentes y aplicarlo a la base; bm . bn = b(m+n)
Producto de cocientes de igual base
Para dividir dos o más potencias que tienen la misma base basta con restar los exponentes y aplicarlo a la base; bm/ bn = bn-m si b es distinto de cero
Potencia de Potencia
Para resolver la potencia de una potencia se multiplican los exponentes y se aplican a la base (bn)m=bn.m
Ley distributiva respecto del producto (a.b)n=an.bn
Ley distributiva respecto del cociente (a/b)n=a/bn si b es distinto de cero
Potencia cero: Por convención b0= 1 ¿A qué será igual 00 ? ¿Existe?
Exponente Negativo: (b)-n=1/bn
Leyes de los signos
Si la base es positiva el resultado es positivo cualquiera sea el exponente
b3=b.b.b
b4=b.b.b.b
Si la base es negativa, el resultado es negativo si el exponente es impar
(-b)3=(-b).(-b).(-b)=-b3
Si la base es negativa, el resultado es positivo si el exponente es par 4
(-b)4=(-b).(-b).(-b).(-b)=-b4
Radicación
La operación de radicación es la inversa de la potenciación, si an = b entonces diremos que n√b= a, donde b es el radicando, n es el índice de la raíz y a es raíz de b.
٠ la raíz es positiva si b es positivo
٠ es negativa si b es negativo y n es impar
Leyes de la radicación
Distributiva respecto del producto y respecto del cociente
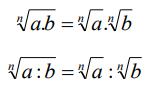
Potencia de una raíz
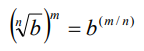
Esto implica que todo índice de una radicación puede escribirse como una potencia de
exponente fraccionario
3.3. Operaciones combinadas de enteros (suma, resta, multiplicación, división y paréntesis)
4. Sistema de numeración decimal y su característica posicional.
Nuestro sistema de numeración tiene dos características esenciales: es decimal y es posicional.
- Es decimal porque:
- Utilizamos 10 dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
- Agrupamos de 10 en 10 en órdenes cada vez mayores:
- 10 U = 1 D
- 10 D = 1 C
- 10 C = 1 UM
- 10 UM = 1DM

En números de nueve cifras esta es la manera como se ordena:

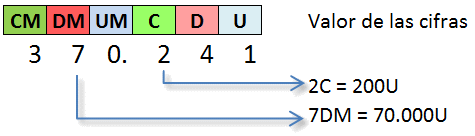
Es posicional porque el valor de cada cifra en un número depende del lugar que ocupa.
En el número 370.241 la cifra 2 ocupa el orden de las centenas, por lo tanto 2C = 20D = 200U
La cifra 7 ocupa el orden de las decenas de millar, por lo tanto 7DM = 70UM = 700C = 7.000D = 70.000U
5. Notación científica
Introducción
La notación científica nos permite escribir números muy grandes o muy pequeños de forma abreviada. Esta notación consiste simplemente en multiplicar por una potencia de base 10 con exponente positivo o negativo.
Ejemplo: el número 0,00000123 puede escribirse en notación científica como
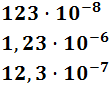
Evitamos escribir los ceros decimales del número, lo que facilita tanto la lectura como la escritura del mismo, reduciendo la probabilidad de cometer erratas.
Obsérvese que existen múltiples posibilidades de expresar el mismo número, todas ellas igualmente válidas.
Veremos cómo escribir números naturales y decimales en notación científica y viceversa.Potencias de 10
Recordatorio del significado y valor de las potencias de base 10 con exponente positivo y con exponente negativo.
![]()
Exponente Positivo
Si n es positivo, la potencia de base 10 con exponente n, es decir, 10n, es el número formado por la cifra 1 seguida de nceros.
Ejemplo:
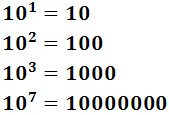
El exponente indica el número de 0's.
Exponente Negativo
La potencia de base 10 con exponente negativo -n, es decir, 10-n, es el número decimal 0,00...01 siendo n el número total de ceros.
Ejemplo:
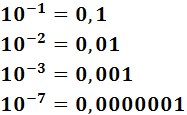
El exponente indica el número de 0's, contabilizando también el cero situado a la izquierda de la coma.
Multiplicar/dividir por 10
La notación científica consiste precisamente en multiplicar por una potencia de 10. En esta sección explicamos el resultado de multiplicar o dividir un número por 10 para comprender el resultado de multiplicar por una potencia de 10.
Multiplicar por 10
Al multiplicar un número por 10, su coma decimal se desplaza una posición hacia la derecha (si no tiene coma, se escribe un 0 a la derecha de la última cifra).
Ejemplo:
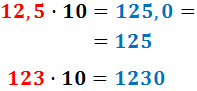
Al multiplicar el número decimal 12,5 por 10, la coma se desplaza una posición hacia la derecha. Como detrás de la coma sólo hay ceros, podemos omitirla.
Al multiplicar el número natural (no decimal) 123 por 10, tenemos que añadirle un 0 a la derecha.
Dividir entre 10
Al dividir un número entre 10, su coma decimal se desplaza una posición hacia la izquierda (si no tiene coma, se introduce a la izquierda de la primera cifra).
Ejemplo:
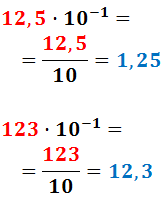
Al dividir el número decimal 12,5 entre 10, la coma se desplaza una posición hacia la izquierda.
Al dividir el número natural (no decimal) 123 entre 10, tenemos que añadirle una coma.
Importante: dividir entre 10 es lo mismo que multiplicar por la potencia de exponente negativo 10-1.
Multiplicar por una potencia de 10 con exponente Positivo
![]()
En el apartado anterior vimos que al multiplicar un número por 10 la coma decimal de dicho número se desplaza una posición hacia la derecha.
Como multiplicar sucesivamente (varias veces) por 10 es lo mismo que multiplicar por una potencia de 10,
Al multiplicar un número por la potencia 10n (con exponente positivo) se desplaza la coma hacia la derecha tantas posiciones como indica el exponente.
Ejemplo:
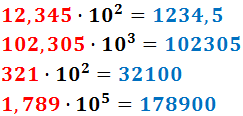
Como los exponentes son positivos, la coma se desplaza hacia la derecha.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la derecha).
Multiplicar por una potencia de 10 con exponente Negativo
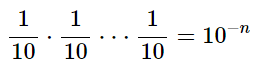
Anteriormente vimos que al dividir un número entre 10 la coma decimal de dicho número se desplaza una posición hacia la izquierda.
Como dividir sucesivamente (varias veces) entre 10 es lo mismo que multiplicar por una potencia de 10 con exponente negativo,
Al multiplicar un número por la potencia 10-n (con exponente negativo) se desplaza la coma hacia la izquierda tantas posiciones como indica el exponente (al cambiarle el signo).
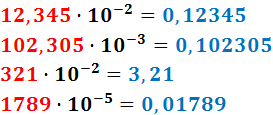
Como los exponentes son negativos, la coma se desplaza hacia la izquierda.
Si no hay suficientes cifras para desplazar la coma, se añaden 0's (a la izquierda). Esto ocurre en el primer, segundo y cuarto número del ejemplo.
Nota: el número resultante al cambiar el signo del exponente indica cuántas posiciones se desplaza la coma:
10-2: dos posiciones hacia la izquierda.
10-3: tres posiciones hacia la izquierda.
10-2: dos posiciones hacia la izquierda.
10-5: cinco posiciones hacia la izquierda.
5.1. Notación Científica Introducción
5.2. Operaciones con números en notación científica: suma, resta, multiplicación, división, potenciación y radicación
La notación científica es una manera rápida de representar un número utilizando raiz cubica y despues con potencia de base diez. Esta notación se utiliza para poder expresar muy fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
siendo:
- a un número mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente.
- n un número entero, que recibe el nombre de exponente u orden de magnitud.
- Suma y resta
Siempre que las potencias de 10 sean las mismas, se deben sumar los coeficientes (o restar si se trata de una resta), dejando la potencia de 10 con el mismo grado. En caso de que no tengan el mismo exponente, debe convertirse el coeficiente, multiplicándolo o dividiéndolo por 10 tantas veces como se necesite para obtener el mismo exponente.
Ejemplos:
- 2×105 + 3×105 = 5×105
- 3×105 - 0.2×105 = 2.8×105
- 2×104 + 3 ×105 - 6 ×103 = (tomamos el exponente 5 como referencia)
- = 0,2 × 105 + 3 × 105 - 0,06 ×105 = 3,14 ×105
Para multiplicar cantidades escritas en notación científica se multiplican los coeficientes y se suman los exponentes.
Ejemplo:
- (4×1012)×(2×105) =8×1017
Para dividir cantidades escritas en notación científica se dividen los coeficientes y se restan los exponentes.
Ejemplo: (48×1010)/(12×101) = 4×109
PotenciaciónSe eleva el coeficiente a la potencia y se multiplican los exponentes.
Ejemplo: (3×106)2 = 9×1012.
RadicaciónSe debe extraer la raíz del coeficiente y se divide el exponente por el índice de la raíz.
Ejemplos:
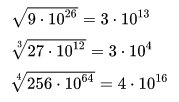
5.3. Operaciones con notación científica
5.4. Aplicación de la notación científica en la medicina, ingeniería, estadística, Física, etc
POTENCIAS Y NOTACIÓN CIENTÍFICA
Si ejemplificamos; al hablar de grandes cantidades de bytes, se puede decir que la capacidad de almacenamiento de datos de una gran computadora es de 500 Terabytes, o sea, una cantidad equivalente a 500 000 000 000 000 bytes.
las cifras del párrafo anterior aparecerían escritas en textos de ciencia y técnica de la forma siguiente:
“La capacidad de almacenamiento de datos de la gran computadora es de 5 x 10^14 bytes .
APLICACIÓN DE LA NOTACIÓN CIENTÍFICA EN LA VIDA DIARIA
En la naturaleza . Además de cantidades muy grandes también están presentes números muy pequeños relacionados a objetos microscópicos.Por ello se utilizan unidades de medida como el micrómetro, el nanómetro y el angstrom .
¿Te imaginas dividir la medida del ojo de una aguja que es de 1 milímetro, en mil partes?. Ese es el tamaño de un micrómetro; es decir la milésima parte de la milésima parte de un metro. Lo que podemos expresar como: 1=0.000001 m. Para poder visualizar el mundo de los micrómetros requerimos del microscopio óptico.
Ahora, el nanómetro es la milésima parte de un micrómetro, ¿puedes imaginarlo? Al compararlo con el metro, tenemos que es la milésima parte de la milésima parte de la milésima parte de un metro, es decir la mil millonésima parte de un metro.
UNA ESCRITURA CORTA PARA UN NÚMERO LARGO
La notación científica es un recurso matemático empleado para simplificar cálculos y representar en forma concisa números muy grandes o muy pequeños. Para hacerlo se usan potencias de diez.
Para expresar un número en notación científica identificamos la coma decimal (si la hay) y la desplazamos hacia la izquierda si el número a convertir es mayor que 10, en cambio, si el número es menor que 1 (empieza con cero coma) la desplazamos hacia la derecha tantos lugares como sea necesario para que (en ambos casos) el único dígito que quede a la izquierda de la coma esté entre 1 y 9 y que todos los otros dígitos aparezcan a la derecha de la coma decimal.