MEDIDA DE LAS FORMAS Y LA REPRESENTACIÓN GRÁFICA DE LOS PROCESOS DE PRODUCCIÓN

NOCIONES DE TRIGONOMETRÍA Y GEOMETRÍA ANALÍTICA (LIBRO PROPORCIONADO POR LA BIBLIOTECA DE KUAA)

ESCUELA DE MATEMÁTICAS UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN

Clasiftcación de los ángulos según su medida

•    Ángulo nulo. Es el ángulo que mide 0^◦.

•    Ángulo agudo. Es el ángulo que mide más de 0^◦ y menos de 90^◦.

•    Ángulo recto.   Es el ángulo que mide exactamente 90^◦.

•    Ángulo obtuso.   Es el ángulo que mide más de 90^◦ y menos de 180^◦.

•    Ángulo llano.   Es el ángulo que mide 180^◦.

Relaciones entre ángulos

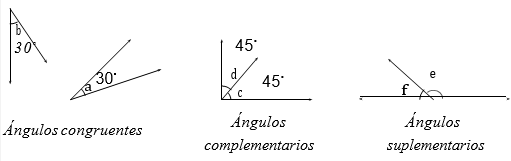
• Ángulos congruentes: decimos que dos ángulos son congruentes si tienen la misma medida.   Si los ángulos α y β son congruentes escribimos α ∼= β.
• Ángulos complementarios: dos ángulos son complementarios si la suma de sus medidas es 90^◦.
• Ángulos suplementarios: dos ángulos son suplementarios si la suma de sus medidas es 180^◦.

Si dos ángulos α y β son complementarios, decimos que α es el ángulo complementario de β. Similarmente si dos ángulos α y β son suplementarios decimos que α es el ángulo suplementario de β.

Ejemplo

Los ángulos a y b que aparecen en la figura son congruentes; los ángulos c y d son complementarios y los ángulos e y f son suplementarios.