SISTEMAS DE NUMERACIÓN, OPERACIONES CON NÚMEROS ENTEROS (Z) Y RACIONALES (Q).
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 1° - Matemáticas |
| Libro: | SISTEMAS DE NUMERACIÓN, OPERACIONES CON NÚMEROS ENTEROS (Z) Y RACIONALES (Q). |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 06:00 |
Tabla de Contenidos
- 1. Sistemas de numeración en las distintas culturas.
- 2. Sistema de numeración binario: Operaciones en el sistema binario (adición, sustracción, multiplicación y división)
- 3. Sistema de numeración sexagesimal: Operaciones en el sistema sexagesimal (adición, sustracción, multiplicación y división)
- 4. Origen de los Enteros.
- 5. Números Racionales (Q) y su representación gráfica.
- 6. Números decimales como consecuencia de los racionales.
- 7. Formas de conversión: de decimal a fracción y de fracción a decimal.
1. Sistemas de numeración en las distintas culturas.
Los números se inventaron por la necesidad de otorgar un símbolo a los objetos cuando queremos cuantificarlos y de ahí vinieron los sistema de numeración.
Cuando pensamos en matemáticas, a muchos nos da un gran dolor de cabeza, pero no debemos perder de vista la importancia de ellas y los avances que generaron en la sociedad y en las culturas de nuestros antepasados, teniendo gran importancia en el comercio, por ejemplo.
Los sistemas de numeración se inventaron por la necesidad de otorgar un símbolo a los objetos cuando queremos cuantificarlos o para saber su valor frente a un intercambio comercial, entre muchas cosas más. Con esta necesidad, las culturas antiguas buscaron la forma en representar esas cuentas por medio de símbolos que se traducen a una cantidad específica, así fue como nacieron algunos de los sistemas de numeración antiguos.
Sistema de numeración egipcio

Sistema de numeración chino

Otra de las culturas más antiguas también tenía su propio sistema de numeración que, igual que los egipcios, era con base en 10. Los diferentes símbolos se componían por agrupaciones de potencias de 10 y se escriben de arriba hacia abajo o de izquierda a derecha y no agrupados. Los símbolo que utilizaban tenían distintivos para su empleo doméstico o comercial. Se necesitaba tener cuidado en cómo agrupar los símbolo porque podían confundirse las unidades, como en el 57 y 75, ya que se escribían de la misma forma.
Sistema de numeración griego

En esta época se empezó a modificar el sistema base 10 para convertirse en acrofónica, en el que en las unidades 5, 10 y 100 se encontraba un distintivo a la palabra que representa la cantidad, como pente (5), deka (10) y mil (1000). De igual manera se utilizaba el principio multiplicativo para el conjunto de unidades.
Posteriormente, el sistema evolucionó a una forma jónica, en la que los números se representaban por las letras del alfabeto griego y otros símbolos, y se encontró una relación entre número y palabras, este tipo de sistema los utilizan también los árabes y los judíos.
Sistema de numeración romano
A diferencia de los sistemas de numeración anteriores, el sistema numérico romano se utiliza en la actualidad. Lo podemos ver en capítulos de libros, escenas de obras de teatro e incluso nombres de autoridades como reyes o Papas. Se caracteriza por utilizar letra mayúsculas como caracteres numéricos, su escritura es de izquierda a derecha.
Sistema de numeración maya
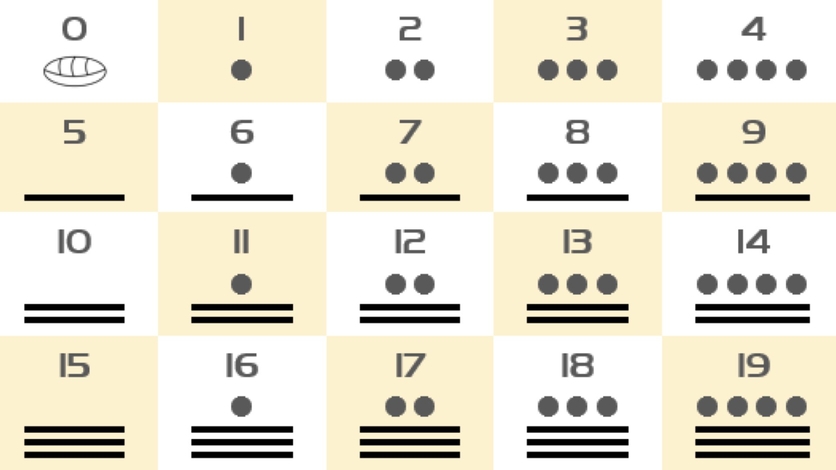
En México también tenemos nuestro propio sistema de numeración antiguo: el desarrollado por los mayas, quienes utilizaron una numeración con base en 520, utilizando el número 5 cómo base auxiliar. Como rasgo distintivo, los mayas fueron los primeros en utilizar el cero como número, es por eso que se cree que el sistema maya es de los mejores utilizados en la antigüedad. Su escritura es de arriba hacia abajo y consta de máximo cuatro filas de elementos, entre ellas los puntos, rayas horizontales y el símbolo del cero.
2. Sistema de numeración binario: Operaciones en el sistema binario (adición, sustracción, multiplicación y división)
Actualmente la mayoría de las personas utilizamos el sistema decimal (de 10 dígitos) para realizar operaciones matemáticas. Este sistema se basa en la combinación de 10 dígitos (del 0 al 9). Construimos números con 10 dígitos y por eso decimos que su base es 10. Por ejemplo el 23, el 234, 1093 etc. Todos son dígitos del 0 al 9.Pero hay otro sistema o lenguaje muy utilizado que es el sistema binario de numeración, que en algunos casos, como por ejemplo en informática, se puede llamar Lenguaje Binario, debido a que es el lenguaje que usamos para entendernos con el ordenador
El sistema binario es un sistema de numeración en el que los números se representan utilizando las cifras 0 y 1, es decir solo 2 dígitos (bi = dos). Esto en informática y en electrónica tiene mucha importancia ya que las computadoras trabajan internamente con 2 niveles: hay o no hay de Tensión, hay o no hay corriente, pulsado o sin pulsar, etc.
Esto provoca que su sistema de numeración natural sea el binario, por ejemplo 1 para encendido y 0 para apagado. También se utiliza en electrónica y en electricidad (encendido o apagado, activado o desactivado, etc.). El lenguaje binario es muy utilizado en el mundo de la tecnología.

Números Binarios
Como ya dijimos, el sistema binario se basa en la representación de cantidades utilizando los números 1 y 0. Por tanto su base es 2 (número de dígitos del sistema). Cada dígito o número en este sistema se denomina bit (contracción de binary digit).
Por ejemplo el número en binario 1001 es un número binario de 4 bits. Recuerda "cualquier número binario solo puede tener ceros y unos".
Los Números Binarios empezarían por el 0 (número binario más pequeño) después el 1 y ahora tendríamos que pasar al siguiente número, que ya sería de dos cifras porque no hay más números binarios de una sola cifra.
El siguiente número binario, por lo tanto, sería combinar el 1 con el 0, es decir el 10 (ya que el 0 con el 1, sería el 01 y no valdría porque sería igual que el 1), el siguiente sería el número el 11. Ahora ya hemos hecho todas las combinaciones posibles de números binarios de 2 cifras, ya no hay más, entonces pasamos a construir los de 3 cifras. El siguiente sería el 100, luego el 101, el 110 y el 111. Ahora de 4 cifras...
Según el orden ascendente de los números en decimal tendríamos los números binarios equivalentes a sus números en decimal :
El 0 en decimal sería el 0 en binario
El 1 en decimal sería el 1 en binario
El 2 en decimal sería el 10 en binario (recuerda solo combinaciones de 1 y 0)
El 3 en decimal sería el 11 en binario

Y así sucesivamente obtendríamos todos los números en orden ascendente de su valor, es decir obtendríamos el Sistema de Numeración Binario y su número equivalente en decimal.
Pero que pasaría si quisiera saber el número equivalente en binario al 23.456 en decimal. Tranquilo, hay un método para convertir un número decimal en binario sin hacerlo uno a uno.
Decimal a Binario
Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).
Para sacar la cifra en binario cogeremos el último cociente (siempre será 1) y todos los restos de las divisiones de abajo arriba, orden ascendente.
Ejemplo queremos convertir el número 28 a binario:
28 dividimos entre 2 : Resto 0
14 dividimos entre 2 : Resto 0
7 dividimos entre 2 : Resto 1
3 dividimos entre 2 : Resto 1 y cociente final 1
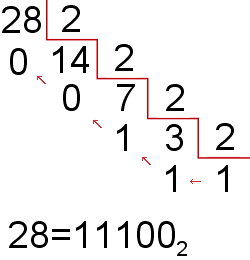
Entonces el primer número del número equivalente en binario sería el cociente último que es 1 y su resto que es también 1, la tercera cifra del equivalente sería el resto de la división anterior que es 1, el de la anterior que es 0 y el último número que cogeríamos sería el resto de la primera división que es 0.
Con todos estos número quedaría el número binario: 11100.
Conclusión el número 28 es equivalente en binario al 11.100.
Vemos como para sacar el equivalente se coge el último cociente de las operaciones y los restos que han salido en orden ascendente (de abajo arriba) 11100.
El subíndice 2 que hemos puesto al final del número en binario, es para indicar que es un número en base 2, pero no es necesario ponerlo.
Veamos otro ejemplo el número 65 pasarlo a binario.
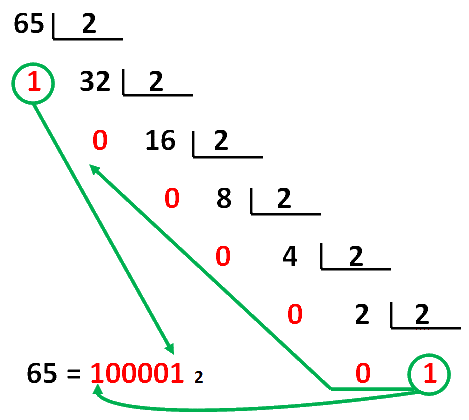
Pues ahora al revés. ¿Que pasaría si quisiera saber cual es el número equivalente en decimal del número binario por ejemplo 1001? Pues también hay método.
PASO 1 – Numeramos los bits de derecha a izquierda comenzando desde el 0 (muy importante desde 0 no desde 1).
PASO 2 – Ese número asignado a cada bit o cifra binaria será el exponente que le corresponde.
PASO 3 – Cada número se multiplica por 2 elevado al exponente que le corresponde asignado anteriormente.
PASO 4 - Se suman todos los productos y el resultado será el número equivalente en decimal
Vamos a verlo paso a paso con un ejemplo y gráficamente que será más sencillo de entender.
Ejemplo el número 1001 queremos saber su equivalente en decimal. Primero asignamos exponentes:
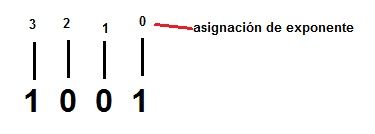
Empezamos por el primer producto, que será el del primer número binario por 2 elevado a su exponente, es decir 1 x 23 .
OJO Recuerda que cualquier número elevado a cero es 1, por ejemplo 2 elevado a 0 es = 1.
El segundo y el tercer productos serán 0 por que 0 x 22 y 0 x 21 su resultado es 0 y el último producto será 1 x 20 que será 1, luego 1 x 20 es 1 (no confundir y poner 0).
Ya estamos en el último paso que es sumar el resultado de todos estos productos:
1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8 + 0 + 0 + 1 = 9
El equivalente en decimal del número binario 1001 es el 9.
Veamos otro ejemplo solo gráficamente para que lo entiendas definitivamente. En este caso la asignación del exponente a cada número ya lo hacemos directamente en los productos, que es como se suele hacer normalmente.
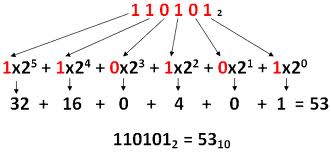
Otro ejemplo con todos los datos:
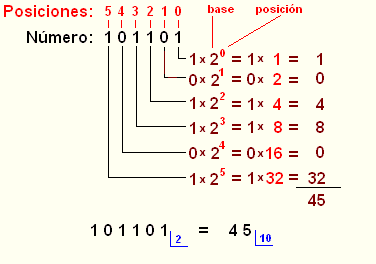
Operaciones Binarias
Las operaciones binarias que se pueden realizar con número binarios son las mismas que en cualquier otro sistema: suma, resta, multiplicación y división. Veamos algunos Ejemplos de Operaciones Binarias.
Suma de Números Binarios
Las posibles combinaciones al sumar dos bits son
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Un ejemplo con más cifras:
100110101
+ 11010101
———————
1000001010
A continuación se suman los números de la siguiente columna: 0 + 0 = 0, pero como nos tenemos que sumar el 1 de la anterior suma, el resultado será 0 + 1 = 1.
Así seguimos hasta terminar todas la columnas (exactamente como en decimal).
Resta de Números Binarios
Las restas básicas 0-0, 1-0 y 1-1 son evidentes:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = Es una resta imposible en binario porque no hay números negativos.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sumándola, a la posición siguiente. Veamos algunos ejemplos:
Dos ejemplos más:
10001 11011001
-01010 -10101011
—————— ————
00111 00101110
Multiplicación de Números Binarios
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Por ejemplo, multipliquemos 10110 por 1001:
10110
x 1001
——————
10110
00000
00000
10110
———————
11000110
División de Números Binarios
Igual que en el producto, la división es muy fácil de realizar, porque no son posibles en el cociente otras cifras que no sean UNOS y CEROS.
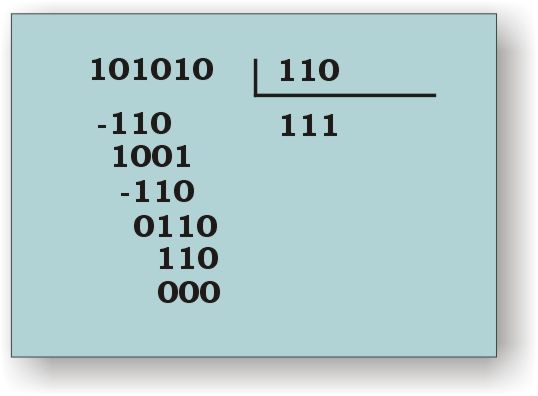
Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).
Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO. En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente.
El procedimiento de división continúa del mismo modo que en el sistema decimal.
2.1. Qué es el sistema binario
3. Sistema de numeración sexagesimal: Operaciones en el sistema sexagesimal (adición, sustracción, multiplicación y división)
El sistema sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades más pequeñas. En otras palabras, se utiliza la base 60.
Este sistema es el utilizado para medidas de tiempo y de ángulos.
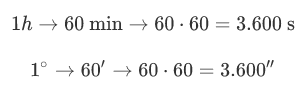
Operaciones con números sexagesimales
Suma
- Paso 1
Colocar los dos números a sumar de la siguiente forma, y sumar columna por columna:

- Paso 2
Si la suma de segundos es superior a 60, dividir el resultado por 60; el resto serán los segundos y el cociente se sumará a los minutos.
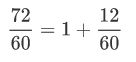
Es decir, el resto es 12 y el cociente 1. Entonces, el resultado se escribe:
![]()
- Paso 3
Repetir el mismo procedimiento para los minutos:
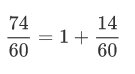
Entonces,
![]()
Resta
- Paso 1
Colocar los dos números a restar uno encima del otro, las horas sobre las horas (o los grados sobre los grados), los minutos sobre los minutos.
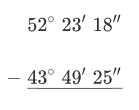
Si la resta de segundos es menor que cero se suman 60” en los segundos y se resta 1’ en los minutos del número de arriba,
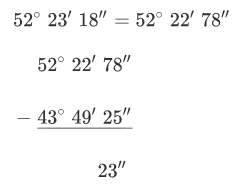
- Paso 2
Repetir el mismo procedimiento con los minutos
Nota: Se resta siempre el mayor número menos el menor. Si se están tratando con ángulos se podría dar el caso de que se deba calcular un ángulo negativo (se hace la resta con valor mayor que cero y se cambia el signo).
Si se opera con medidas temporales no tiene mucho sentido obtener tiempos negativos. No obstante en la resolución de un problema en el que se defina una referencia de tiempo t=0, se puede obtener un tiempo negativo para un instante anterior.
Multiplicación por un número
- Paso 1
Multiplicar segundos, minutos y horas (o grados) por el número:

- Paso 2
Si se obtienen más de 60 segundos, dividir por 60 y el resto serán los segundos y el cociente se añadirá a los minutos
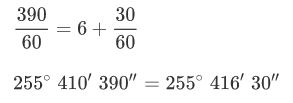
- Paso 3
Repetir el mismo procedimiento para los minutos
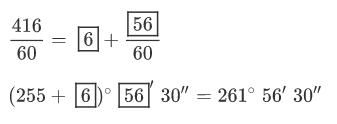
División por un número
Se pretende dividir 37° 48” 25’ por 5
- Paso 1
Se empiezan dividiendo las horas (o grados) por el número:
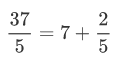
El cociente, 7, son las horas y el resto multiplicado por 60,( 2 x 60 ) ,se añadirá a los minutos.
- Paso 2
Se repite el mismo procedimiento con los minutos
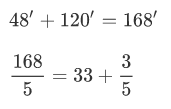
33 serán los minutos finales, y el resto multiplicado por 60 se añadirá ( 3 x 60 ) a los segundos.
- Paso 3
Por último, se repite el mismo procedimiento con los segundos
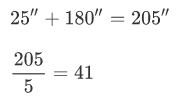
Entonces, el resultado final será:
![]()
Nota: La última división podría dar un resto no nulo. En tal caso, los segundos se expresarían con decimales.
4. Origen de los Enteros.
EL ORIGEN DE LOS NUMEROS ENTEROS
El hombre desde principios de la evolución siempre utilizó recursos para facilitar su relación con el medio que lo rodea; para contar cantidades utilizaba piedras, hacía marcas en los arboles o nudos en sogas. Desde la era primitiva el hombre siempre buscó respuestas a sus inquietudes. La inquietud permitió la aparición de conceptos abstractos en la mente del hombre primitivo ya evolucionado. Cuando el hombre desarrolla la capacidad de darle sentido racional a las cosas, nace el concepto de cantidad.
El hombre primitivo sólo era capaz de distinguir entre una cosa o muchas. Durante el proceso de hominización, a medida que aumenta su capacidad de abstracción, aprende a contar. El pensamiento matemático nació por la necesidad de enumerar las reses, contabilizar objetos y controlar el paso del tiempo. Para ninguna de estas actividades era preciso el cero. Contar es identificar los elementos de un conjunto, por ejemplo piedras, con un subconjunto {1,2,...,n} de los números naturales. Los números naturales cuentan y ordenan: uno, dos, tres, cuatro...
Los números naturales, no son suficientes cuando se quiere fijar una referencia. Es el caso de la temperatura ambiente o los tratos comerciales. Una deuda no se puede representar con un número natural, además el frío y el calor deben medirse en relación con algo. Hay que inventar una referencia y la manera de contar a ambos lados de esta: es el número cero, los naturales positivos y los negativos. El número cero apareció en Mesopotamia hacia el siglo III a.C., sin embargo, su primer cometido fue el de un dígito sin contenido, un posicionador, para diferenciar unas cantidades de otras. (por ejemplo, 1 de 10). Los números enteros cuentan respecto a una referencia: menos dos, menos uno, cero, uno, dos...
Se sabe que los números naturales se pueden sumar y multiplicar, pero no todos se pueden restar o dividir; este hecho trajo como consecuencia la extensión del conjunto de los naturales. El hombre, visto en la imposibilidad de realizar, en general, la operación de resta crea otro conjunto, que viene hacer el conjunto de los números negativos, conocidos antiguamente como “números deudos” o “números absurdos”, que datan de una época donde el interés central era la de convivir con los problemas cotidianos a la naturaleza.
Hoy en día, los números enteros representan una generalización del conjunto de números naturales que incluye números negativos (resultados de restar a un número natural otro mayor además del cero). Así los números enteros están formados por un conjunto de enteros positivos que podemos interpretar como los números naturales convencionales, el cero, y un conjunto de enteros negativos que son los opuestos de los naturales (éstos pueden ser interpretados como el resultado de restar a 0 un número natural).
¿Quién inventó los números?
Los enteros se representan gráficamente en la recta de números enteros como puntos a un mismo espacio entre sí desde menos infinito, ..., -3 , -2, -1, 0, 1, 2, 3,... hasta más infinito: los números enteros no tienen principio ni fin.
Los números negativos pueden aplicarse en distintos contextos, como la representación de deudas, profundidades bajo el nivel del mar, temperaturas bajo cero, entre otros. Inicialmente el primer campo de aplicación fue la contabilidad donde los números negativos significaban deudas y los positivos haberes o activos poseídos. El hecho de que un número sea entero, significa que no tiene parte decimal. Imaginemos que disponemos de dos barras de chocolate, cada una con tres divisiones, las cuales van a repartirse entre tres personas. Es claro que esta operación puede realizarse convenientemente si a cada persona le tocan dos partes de las tres que tiene cada barra. Ahora bien, imaginemos que tenemos 7 balines (esferas de metal) que queremos repartir entre las mismas tres personas. Es claro que no puede partirse un balín para que a cada persona le toque la misma cantidad de balines, así que a cada uno le deben tocar dos balines y regalar uno para que la repartición sea justa, o bien conseguir otros dos balines para que a cada uno le toquen tres.
REPRESENTANDO LOS NÚMEROS ENTEROS
El conjunto de los números enteros se representa comúnmente como una serie de valores discretos marcados sobre una recta. Así, los números enteros no llenan la recta, sino que entre ellos existen infinitos puntos que no pertenecen a dicho conjunto. En esta distribución, se dice que, dados dos números enteros n y m, n es mayor o igual que m (n > m) si n - m es un número entero positivo o cero. En virtud de ello, el de los números enteros es un conjunto ordenado.
Los números enteros son positivos cuando se ubican a la derecha del cero en la recta numérica y se obtienen poniendo el signo + (más) delante de un número natural. Son negativos cuando están a la izquierda del cero, y se obtienen al poner el signo - (menos) delante de un número natural.
De esta manera tenemos dos conjuntos:
• Conjunto de números enteros positivos
• Conjunto de números enteros negativos
Los números enteros acotan todo lo que nos rodea, con pruebas sencillas podemos experimentar su aplicación en la vida cotidiana, desde la utilización de estos para medir distancias y temperaturas, hasta la encriptación del comercio electrónico y el cálculo del número de asistentes a una manifestación.
Mas información https://ue.aprendiendomas.com.bo/pluginfile.php/129/mod_book/chapter/637/numeros-enteros-origen-e-historia.pdf
4.1. Operaciones en Z: Adición y sustracción, multiplicación y división, sus propiedades aplicadas a la vida cotidiana.
Suma de números enteros
1. Si los números enteros tienen el mismo signo, se suman los valores absolutos y al resultado se le coloca el signo común.
3 + 5 = 8
(−3) + (−5) = − 8
2. Si números enteros son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le coloca el signo del número de mayor valor absoluto.
− 3 + 5 = 2
3 + (−5) = − 2
Propiedades de la suma de números enteros1. Interna:
a + b ϵ ℜ
3 + (−5) = -2
2. Asociativa:
(a + b) + c = a + (b + c) ·
(2 + 3) + (− 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0 = 0
3. Conmutativa:
a + b = b + a
2 + (− 5) = (− 5) + 2
− 3 = − 3
4. Elemento neutro:
a + 0 = a
(−5) + 0 = − 5
5. Elemento opuesto
a + (-a) = 0
5 + (−5) = 0
−(−5) = 5
Resta de números enterosLa diferencia de los números enteros se obtiene sumando al minuendo el opuesto del sustraendo.
a - b = a + (-b)
7 − 5 = 2
7 − (−5) = 7 + 5 = 12
Propiedades de la resta de números enteros
1.Interna:
a − b ϵ ℜ
10 − (−5) =15
2. No es Conmutativa:
a - b ≠ b - a
5 − 2 ≠ 2 − 5
Multiplicación de números enterosLa multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
Regla de los signos
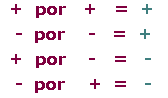
2 · 5 = 10
(−2) · (−5) = 10
2 · (−5) = − 10
(−2) · 5 = − 10
Propiedades de la multiplicación de números enteros
1. Interna:
a · b ϵ ℜ
2 · (−5) =-10
2. Asociativa:
(a · b) · c = a · (b · c)
(2 · 3) · (−5) = 2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
3. Conmutativa:
a · b = b · a
2 · (−5) = (−5) · 2
-10 = -10
4. Elemento neutro:
a ·1 = a
(−5)· 1 = (−5)
5. Distributiva:
a · (b + c) = a · b + a · c
(−2)· (3 + 5) = (−2) · 3 + (−2) · 5
(−2)· 8 =- 6 - 10
-16 = -16
6. Sacar factor común:
a · b + a · c = a · (b + c)
(−2) · 3 + (−2) · 5 = (−2) · (3 + 5)
División de números enterosLa división de dos números enteros es otro número entero, que tiene como valor absoluto el cociente de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Propiedades de la división de números enteros1. No es una operación interna:
(−2) : 6 No pertenece enteros
2. No es Conmutativo:
a : b ≠ b : a
6 : (−2) ≠ (−2) : 6
4.2. Operaciones en Z: Potenciación y radicación, sus propiedades aplicadas a la tecnología.
Potencia de números enterosLa potencia de exponente natural de un número entero es otro número entero, cuyo valor absoluto es el valor absoluto de la potencia y cuyo signo es el que se deduce de la aplicación de las siguientes reglas:
1. Las potencias de exponente par son siempre positivas.
2. Las potencias de exponente impar tienen el mismo signo de la base.
Propiedadesa0 = 1 ·
a1 = a
am · a n = am+n
(−2)5 ·(−2)2 = (−2)5+2 = (−2)7 = −128
am : a n = am - n
(−2)5 : (−2)2 = (−2)5 - 2 = (−2)3 = −8
(am)n = am · n
[(−2)3]2 = (−2)6 = 64
an · b n = (a · b) n
(−2)3 · (3)3 = (−6) 3 = −216
an : b n = (a : b) n
(−6)3 : 3 3 = (−2)3 = −8
Potencias de exponente entero negativo
![]()
Raíz cuadrada de un número entero
Las raíces cuadradas de números enteros tienen dos signos: positivo y negativo.
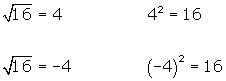
El radicando es siempre un número positivo o igual a cero, ya que se trata del cuadrado número.
![]()
Operaciones combinadas con números enteros
Prioridades en las operaciones
1º.Efectuar las operaciones entre paréntesis, corchetes y llaves..
2º.Calcular las potencias y raíces.
3º.Efectuar los productos y cocientes.
4º.Realizar las sumas y restas.
5. Números Racionales (Q) y su representación gráfica.
Un número racional es todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por .
.
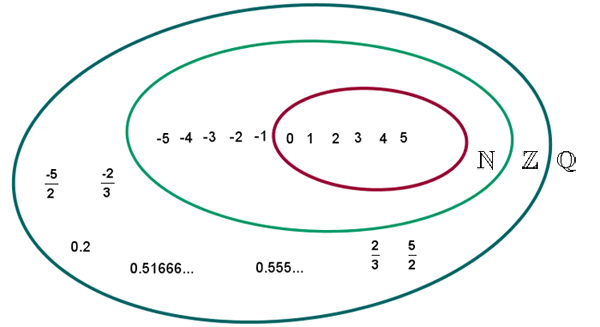
Representación de números racionales
Los números racionales se representan en la recta junto a los números enteros.
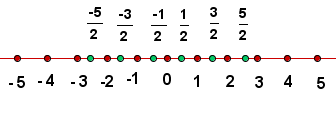
Para representar con precisión los números racionales:
1Tomamos un segmento de longitud la unidad, por ejemplo.
2Trazamos un segmento auxiliar desde el origen y lo dividimos en las partes que deseemos. En nuestro ejemplo, lo dividimos en 4 partes.
3Unimos el último punto del segmento auxiliar con el extremo del otro segmento y trazamos segmentos paralelos en cada uno de los puntos, obtenidos en la partición del segmento auxiliar.
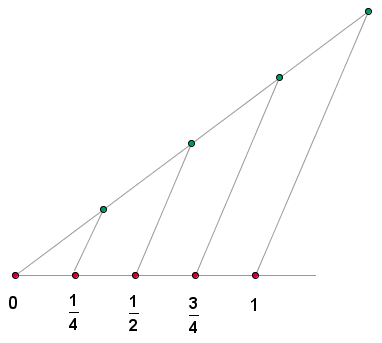
En la práctica se utilizan número racional y fracción como sinónimos.
5.1. Relación de orden de los números racionales.
Al igual que los números enteros, los números racionales también pueden ser localizados en la recta numérica para su ordenación. Por ejemplo, en la figura 5 se muestran los números racionales 18 y 58.
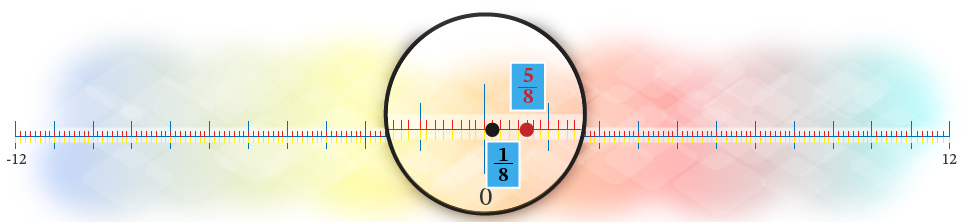
Se observa que el número 18se encuentra a la izquierda de 58, por lo que 18 es menor que 58, es decir:
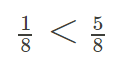
En la figura se muestra la relación de orden entre los números 18 y 58

5.2. Operaciones en Q: Adición y sustracción, multiplicación y división, sus propiedades aplicadas a la vida cotidiana
Suma y resta de números racionales
Con el mismo denominador
Se suman o se restan los numeradores y se mantiene el denominador.
![]()
![]()
![]()
![]()
Con distinto denominador
En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
![]()
![]()
![]()
![]()
Propiedades de la suma de números racionales
1. Interna:
a + b ϵ Q
2. Asociativa:
(a + b) + c = a + (b + c) ·
![]()
![]()
![]()
3. Conmutativa:
a + b = b + a
![]()
![]()
4. Elemento neutro:
a + 0 = a
![]()
5. Elemento opuesto
a + (−a) = 0
![]()
El opuesto del opuesto de un número es igual al mismo número.
![]()
Multiplicación de números racionales
![]()
![]()
Propiedades de la multiplicación de números racionales
1. Interna:
a · b ϵ Q
2. Asociativa:
(a · b) · c = a · (b · c)
![]()
![]()
3. Conmutativa:
a · b = b · a
![]()
4. Elemento neutro:
a ·1 = a
![]()
5. Elemento inverso:
![]()
![]()
6. Distributiva:
a · (b + c) = a · b + a · c
![]()
![]()
a · b + a · c = a · (b + c)
![]()
División de números racionales
![]()
![]()
5.3. Operaciones en Q: Potenciación y radicación, sus propiedades aplicadas a la tecnología.
Potencias de números racionales
Potencias de exponente entero y base racional
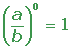
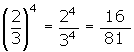
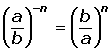
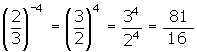
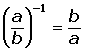
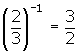
Propiedades
1.
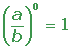
2.
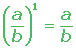
3. Producto de potencias con la misma base:
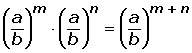
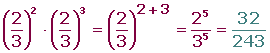
4. División de potencias con la misma base:
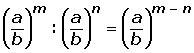
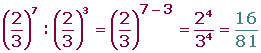
5. Potencia de una potencia:
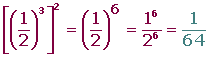
6. Producto de potencias con el mismo exponente:
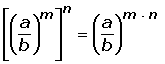
![]()
7. Cociente de potencias con el mismo exponente:
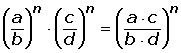
![]()
6. Números decimales como consecuencia de los racionales.
Un número decimal es aquel que se puede expresar mediante una fracción decimal.
Consta de dos partes: entera y decimal.
![]()
Para expresar un número decimal como una fracción decimal, se pone como numerador de la fracción el número dado sin la coma y como denominador la unidad seguida de tantos ceros como cifras decimales tenga ese número.
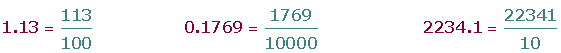
Clasificación de números decimales
Decimal exacto
La parte decimal de un número decimal exacto está compuesta por una cantidad finita de términos.
![]()
Periódico puro
La parte decimal, llamada periodo, se repite infinitamente.
![]()
Periódico mixto
Su parte decimal está compuesta por una parte no periódica y una parte periódica o período.
![]()
No exactos y no periódicos
![]()
7. Formas de conversión: de decimal a fracción y de fracción a decimal.
Convertir Decimales a Fracciones
Para convertir un Decimal a una Fracción sigue estos pasos:
Paso 1: Escribe el decimal dividido por 1.
Paso 2: Multiplica los números de arriba y abajo por 10 una vez por cada número luego de la coma. (Por ejemplo, si hay dos números luego del decimal, multiplícalos por 100, si hay tres usa el 1000, etc.)
Paso 3: Simplifica (reduce) la fracción
Ejemplo 1: Expresar 0,75 como fracción
Paso 1: Escribe:
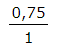
Paso 2: Multiplica el numero de abajo y el de arriba por 100 (porque hay 2 dígitos luego de la coma):
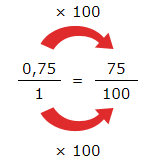
Paso 3: Simplifica la fracción:
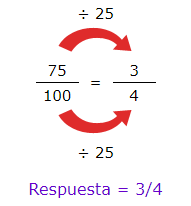
Convertir de fracción a decimal
Para convertir una fracción a un número decimal debemos dividir el numerador entre el denominador, por ejemplo, supongamos que deseamos transformar la fracción 5/8 a decimal. Cuando dividimos 5 entre 8 el obtenemos como resultado 0,625, éste es el número decimal que es equivalente a la fracción 5/8. Veamos otros ejemplos:
- Sea la fracción 4/3, cuando dividimos 4 entre 3 obtenemos 1,333333, el cual es un número decimal que no se detiene, en otras palabras, un número periódico. El período lo podemos expresar escribiendo un arco o barra encima de las cifras repetidas, por lo tanto, éste indicará que el número se repite indefinidamente. Entonces, 1,͞3 es el número decimal equivalente a la fracción 4/3.
- Sea la fracción 3 5/11; como podemos observar es una fracción mixta, ya que está compuesta por un número entero y una fracción. Para transformarla a un decimal podemos realizar dos procedimientos:
- Convirtiendo primero la parte fraccionaria a un decimal y a continuación, agregamos la parte entera a él:
5 ÷ 11 = 0, ͞͞͞4͞5 → 3, ͞͞͞4͞5
- Convirtiendo la fracción mixta a una fracción propia, luego, dividimos el numerador entre el denominador:
3 5/11 = (3 × 11 + 5) / 11 = 38/11
38 ÷ 11 = 3, ͞͞͞4͞5
7.1. Convertir fracción en decimal
7.2. Convertir un decimal exacto a fracción
7.3. Convertir decimal periódico puro a fracción | Método 2