FUERZAS EN EQUILIBRIO ESTÁTICO EN LA MADRE TIERRA Y EL COSMO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Ciencias Naturales: Física |
| Libro: | FUERZAS EN EQUILIBRIO ESTÁTICO EN LA MADRE TIERRA Y EL COSMO |
| Impreso por: | Invitado |
| Fecha: | viernes, 7 de marzo de 2025, 03:30 |
1. Fuerza y tipos de fuerzas en la naturaleza.
¿Qué es la fuerza?
Su palabra proviene del latín fortia. La fuerza es la capacidad para realizar un trabajo físico o un movimiento, así como también la potencia o esfuerzo para sostener un cuerpo o resistir un empuje. Los efectos que puede tener una fuerza son que un cuerpo se deforme (por ejemplo, si apretamos o estiramos un trozo de goma de mascar); que un cuerpo permanezca en reposo (por ejemplo, para mantener estirado un puente, hay que hacer fuerza sobre él), y que cambie su estado de movimiento (ya sea cuando el objeto este estático, o acelerarlo o frenarlo cuando se esté moviendo).
En el campo de la física, la fuerza es una magnitud vectorial, y es toda causa capaz de cambiar el estado de reposo o de movimiento de un cuerpo. La fuerza que actúa sobre un objeto de masa m es igual a la variación del momento lineal (o cantidad de movimiento) de dicho objeto respecto del tiempo. La unidad de fuerza en el Sistema Internacional (SI) es el newton, de símbolo N. El concepto de fuerza se suele explicar matemáticamente en términos de las tres leyes del movimiento de Newton.
En una fuerza pueden tenerse en cuenta diferentes rasgos determinantes: el punto de aplicación (punto del cuerpo sobre el que se ejerce la fuerza); la dirección (recta sobre la que la fuerza induce a moverse al cuerpo); el sentido (orientación de la fuerza) y la intensidad (medida de la fuerza respecto a una unitaria establecida).
Existen dos tipos de fuerzas; las que actúan por contacto, en donde el cuerpo que ejerce la fuerza está en contacto directo con el cuerpo sobre el que esta se aplica, por ejemplo: lanzar una piedra, tirar de una cuerda, etc. Y las que actúan a distancia, aquí el cuerpo el cuerpo que ejerce la fuerza no está en contacto con el cuerpo sobre el que esta se aplica, ejemplo: la fuerza de atracción magnética, la fuerza con que la Tierra atrae a los cuerpos, etc.
Tipos de Fuerzas en la naturaleza
La mayoría de los fenómenos que ocurren en la naturaleza pueden ser explicados a través de cuatro interacciones que ocurren en la naturaleza. Fenómenos tales como el movimiento de los planetas, cometas y otros astros en torno al Sol, el movimiento de las cargas en un conductor que inducen a un campo magnético, las fuerzas de atracción que experimentan los electrones en torno al núcleo, la utilización de la energía de los núcleos atómicos, entre muchos otros sucesos, ocurren gracias a la acción de cuatro fuerzas.
En la naturaleza, existe la interacción de cuatro fuerzas a saber: la fuerza gravitacional, la fuerza nuclear fuerte, la fuerza electromagnética y la interacción débil.
Así mismo, según Young y Freedman (2009) “las partículas se clasifican de acuerdo con sus interacciones”. por lo tanto existen para cada interacción, un tipo de partícula específica.
Entre las características de las interacciones de las fuerzas fundamentales en la naturaleza se encuentran:
Fuerza gravitacional: Todos los cuerpos son atraídos por una fuerza que es directamente proporcional a sus masas, e inversamente proporcional al cuadrado de la distancia que los separa. La fuerza gravitacional es la causante de que los cuerpos caigan y del movimiento de los cuerpos celestes que se encuentran en el universo: planetas, satélites, estrellas, galaxias, cometas, entre otros. Su partícula mediadora es el gravitón. Posee un radio de acción infinito.
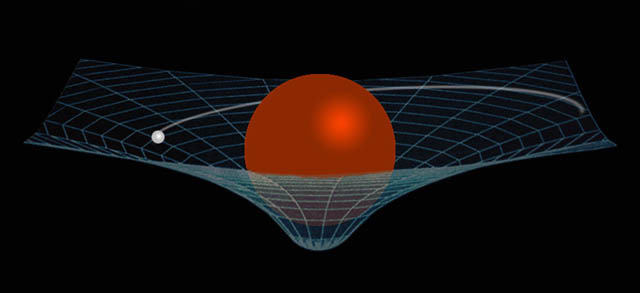
Interacción electromagnética: Es considerada la fuerza que actúa sobre las partículas con carga eléctrica. Toda carga en movimiento produce un campo magnético a su alrededor y es de naturaleza atractiva o repulsiva, dependiendo de las cargas. La partícula mediadora es el fotón. Al igual que la interacción gravitacional, posee un radio de acción infinito.
Interacción nuclear fuerte: Es la interacción más fuerte que existe y permite mantener los nucleones (protones y neutrones), en interacción. Se refiere a la interacción que mantiene unidos a los quarks para formar hadrones, (protones, neutrones y mesones), por lo tanto permite mantener el núcleo unidos. Esta fuerza es la responsable de la estabilidad en toda la materia (Román). La partícula mediadora en esta interacción es el gluón. “Son fuerzas de corto alcance, actúan sólo a distancias que tienen las dimensiones del núcleo atómico”. (Zubero, 2010).
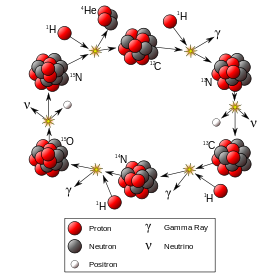
Interacción nuclear débil: Este tipo de fuerza es responsable de la desintegración beta de los núcleos de los átomos. Esta interacción es de corto alcance, es decir, distancias menores que las dimensiones del núcleo.
“Es la interacción responsable de que un quark de un tipo se transforme en un quark de otro tipo como ocurre en la desintegración Beta de los núcleos”. (Zubero, 2010). La partícula mediadora son los bosones.
más información sobre fuerzas de la naturaleza....
para más información click en el link https://ue.aprendiendomas.com.bo/pluginfile.php/537/mod_book/chapter/3010/FN%20PDF.pdf
2. Condiciones de equilibrio y su interrelación en los procesos socio productivos.
Condiciones de equilibrio
as condiciones de equilibrio son las leyes que rigen la estática. La estática es la ciencia que estudia las fuerzas que se aplican a un cuerpo para describir un sistema en equilibrio. Diremos que un sistema está en equilibrio cuando los cuerpos que lo forman están en reposo, es decir, sin movimiento. Las fuerzas que se aplican sobre un cuerpo pueden ser de tres formas:
- Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.
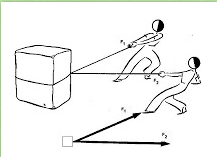
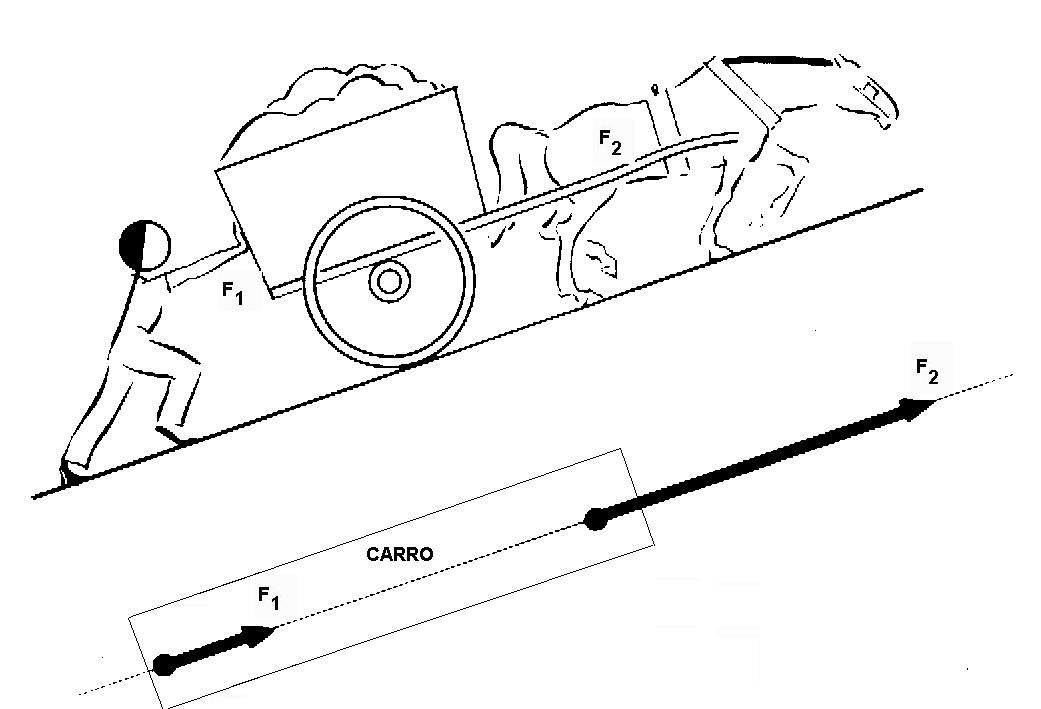
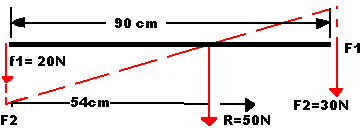
- Primera condición de equilibrio: Diremos que un cuerpo se encuentra en equilibrio de traslación cuando la fuerza resultante de todas las fuerzas que actúan sobre él es nula: ∑ F = 0.
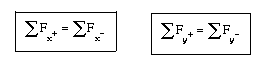
Desde el punto de vista matemático, en el caso de fuerzas coplanarias, se tiene que cumplir que la suma aritmética de las fuerzas o de sus componentes que están el la dirección positiva del eje X sea igual a las componentes de las que están en la dirección negativa. De forma análoga, la suma aritmética de las componentes que están en la dirección positiva del eje Y tiene que ser igual a las componentes que se encuentran en la dirección negativa:
Por otro lado, desde el punto de vista geométrico, se tiene que cumplir que las fuerzas que actúan sobre un cuerpo en equilibrio tienen un gráfico con forma de polígono cerrado; ya que en el gráfico de las fuerzas, el origen de cada fuerza se representa a partir del extremo de la fuerza anterior, tal y como podemos observar en la siguiente imagen.
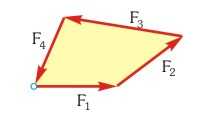
El hecho de que su gráfico corresponda a un polígono cerrado verifica que la fuerza resultante sea nula, ya que el origen de la primera fuerza (F1) coincide con el extremo de la última (F4).
- Segunda condición de equilibrio: Por otro lado, diremos que un cuerpo está en equilibrio de rotación cuando la suma de todas las fuerzas que se ejercen en él respecto a cualquier punto es nula. O dicho de otro modo, cuando la suma de los momentos de torsión es cero.
Un cuerpo se encuentra en equilibrio traslacional y rotacional cuando se verifiquen de forma simultánea las dos condiciones de equilibrio. Estas condiciones de equilibrio se convierten, gracias al álgebra vectorial, en un sistema de ecuaciones cuya solución será la solución de la condición del equilibrio.
3. Equilibrio estático de la partícula
Condiciones de equilibrio estático de una partícula
Definición
Una partícula está en equilibrio estático cuando se encuentra en reposo o se desplaza con MRU, es decir cuando su aceleración es igual a cero.
Condición de equilibrio
Para que una partícula esté en equilibrio la resultante de fuerzas (o la suma vectorial de fuerzas) aplicadas debe ser igual a 0.
![]()
En el plano, podemos decir que el sistema se encuentra en equilibrio si la suma de fuerzas en X y la suma de fuerzas en Y equivalen a cero.
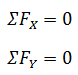
Cuando tenemos un sistema de fuerzas aplicadas a una partícula con diferentes direcciones, lo que podemos hacer es descomponer las fuerzas aplicadas en los ejes X e Y (es decir proyectar las fuerzas sobre los dos ejes) y plantear luego las ecuaciones de equilibrio anteriores.
Ver más sobre equilibrio de una particula
Más información ...https://ue.aprendiendomas.com.bo/pluginfile.php/537/mod_book/chapter/3012/equilibrio-de-particula.pdf
4. Equilibrio estático del sólido rígido
Equilibrio estático del sólido rígido
Se define el sólido rígido como un cuerpo extenso e indeformable, de modo que las posiciones relativas de las partículas que lo constituyen se mantienen invariables.
Como el sólido rígido es un caso particular de sistema de partículas, podemos aplicar los teoremas del capítulo anterior, en particular, haremos uso del teorema del momento angular de un sistema de partículas que relaciona el momento angular del sistema, con el momento total de las fuerzas exteriores que actúan sobre dicho sistema.
Del mismo modo, nos basaremos en el capítulo previo para obtener la expresión del teorema de la energía para un sólido rígido teniendo en cuenta que el trabajo realizado por las fuerzas interiores es cero
Este es el capítulo se presenta de nuevo la ocasión al estudiante de adquirir la habilidad de describir las interacciones por fuerzas, de plantear las ecuaciones del movimiento, aplicar el principio de conservación del momento angular, el balance energético de una situación dinámica identificando los cambios energéticos y calculándolos empleando la fórmula apropiada.
Centros de masa y momentos de inercia
La fórmula que nos permite determinar la posición del centro de masas de un sistema de partículas se ha estudiado en el capítulo anterior. En este capítulo calcularemos el centro de masas de sólidos homogéneos sencillos ya que en el procedimiento de cálculo del centro de masas, los estudiantes suelen tener dificultades en la elección del elemento diferencial y en el cálculo de la longitud, área o volumen de dicho elemento, antes de relacionar las variables que intervienen, y efectuar la integración. La misma dificultad se presenta en el cálculo de los momentos de inercia.
Hay dos formas de introducir el concepto de momento de inercia de un sólido en rotación en torno a un eje fijo:
A través de la fórmula de la energía cinética de rotación.
A través del momento angular de un sólido en rotación en torno a cualquier eje.
La primera aproximación es más simple, pero se considera más apropiada la segunda.
El cálculo de los momentos de inercia se limitará a los casos más simples, el más importante es el momento de inercia de un disco respecto de un eje perpendicular al plano que pase por el centro. Podemos considerar tres clases de problemas:
Cálculo del momento de inercia de forma directa.
Cálculo del momento de inercia del cuerpo a partir de un disco elemental. Por ejemplo, el momento de inercia de un cono macizo o de una esfera respecto de su eje de simetría.
Aplicación del teorema de Steiner.
Conservación del momento angular
Los principios de conservación son esenciales en Física. En capítulo anterior se aplicó el principio de conservación del momento lineal a las colisiones. En este capítulo se resolverán problemas de aplicación del principio de conservación del momento angular, razonándose en términos de fuerzas exteriores y momentos el por qué de tal aplicación. Se mencionarán situaciones de la vida diaria que son explicadas por dicho principio. Los problemas más significativos son aquellos en los que una partícula choca contra un sólido en rotación en torno a un eje fijo.
Dinámica del sólido rígido
Rotación
Se resolverán problemas propuestos en la lección de Dinámica, pero ahora con poleas con masa no despreciable, para comprobar su efecto en el movimiento del sistema. Por ejemplo, la máquina de Atwood.
Se resolverán ejercicios en los que intervengan cuerpos que deslizan, a lo largo de planos inclinados unidos por cuerdas que pasan a través de poleas. Se plantearán las ecuaciones de la dinámica de cada cuerpo, ampliando el diagrama extendido de fuerzas, para incluir el movimiento de rotación. Por último, se establecerán las relaciones entre las aceleraciones angulares y lineales.
Se efectuará el balance energético, comparando la situación inicial y la final, identificando los distintos cambios de energía, calculándolos empleando la fórmula apropiada, y hallando el trabajo de las fuerzas disipativas. Se comprobará que los resultados coinciden con los obtenidos en el planteamiento dinámico del problema.
Movimiento de rodar sin deslizar
Una cuestión que produce confusión en los estudiantes se refiere al papel de la fuerza de rozamiento en el movimiento de rodar, y la diferencia entre esta fuerza y la que se produce en el deslizamiento. Es necesario plantear varios ejemplos, para que los estudiantes asimilen que dicha fuerza de rozamiento es una incógnita a resolver en las ecuaciones del movimiento. Por otra parte, como el punto de contacto está instantáneamente en reposo, el rozamiento existente es rozamiento estático que es menor que el límite máximo μsN , para que el sólido ruede sin deslizar. Algunos autores proponen, para evitar confusiones, dar distintos nombres a ambos tipos de fuerzas de rozamiento.
Los estudiantes suelen incluir el trabajo de la fuerza de rozamiento del movimiento de rodar en el balance energético. Puesto que el rozamiento es estático, no existe disipación de energía mecánica.
Como ejemplo significativo se les puede proponer a los estudiantes que razonen desde el punto de vista cualitativo cuál de estos tres sólidos: un aro, un cilindro y una esfera, que parten desde la misma altura en un plano inclinado llegará antes al final de dicho plano.
Otra cuestión que no se suele demostrarse en los libros de texto, es la ecuación que relaciona el momento angular respecto del centro de masas con el momento de las fuerzas respecto a dicho punto es válida incluso cuando el centro de masas es el origen de un sistema no inercial.
DLcm/Dt=Mcm
Se resolverán ejercicios en los que intervengan cuerpos que deslizan, que ruedan sin deslizar, a lo largo de planos inclinados unidos por cuerdas que pasan a través de poleas. Se plantearán las ecuaciones de la dinámica de cada cuerpo, ampliando el diagrama extendido de fuerzas, para incluir el movimiento de rotación .Por último, se establecerán las relaciones entre las aceleraciones angulares y lineales.
Se efectuará el balance energético, comparando la situación inicial y la final, identificando los distintos cambios de energía, calculándolos empleando la fórmula apropiada y hallando el trabajo de las fuerzas disipativas. Se comprobará que los resultados coinciden con los obtenidos en el planteamiento dinámico del problema.
Estática
La Estática es la parte de la Mecánica que trata del equilibrio de los cuerpos bajo la acción de fuerzas. El término equilibrio significa que el cuerpo se encuentra en reposo, o bien que se está moviendo a velocidad constante. En esta sección se analiza las condiciones bajo las cuales un cuerpo se encuentra en equilibrio.
Se estudiará el equilibrio de una partícula, y de uno o más sólidos rígidos. El número de situaciones que se pueden plantear es muy grande y los problemas pueden llegar a ser complicados, saliéndose de la Física básica y entrando en una asignatura de especialidad. Los límites estarían en estudiar el equilibrio de como máximo dos cuerpos rígidos, sujetos por cuerdas, apoyados en planos y/o articulados.
Como ya se indicó en el capítulo de Dinámica se debe de seguir una cierta estrategia en la resolución de problemas, en el caso de la Estática consiste en:
Identificar la partícula, o el cuerpo cuyo equilibrio se va a estudiar.
Sustituir las diversas interacciones por fuerzas, dibujando el vector correspondiente en su punto de aplicación.
Aplicar las condiciones de equilibrio.
Resolver el sistema de ecuaciones, despejando las incógnitas.
Cuando hay más de un sólido en equilibrio, se deberá estudiar cada cuerpo separadamente identificando correctamente los pares de acción-reacción.
Más información https://ue.aprendiendomas.com.bo/pluginfile.php/537/mod_book/chapter/3013/EE.pdf
video de ejercicio
5. *Máquinas simples y sus beneficios para la comunidad.
Las máquinas simples se usan para multiplicar la fuerza o, como se señaló, para cambiar su dirección; la idea es siempre que el trabajo demande menos esfuerzo y que resulte entonces más sencillo, y en ocasiones también más seguro. En suma, las máquinas simples se utilizan para transformar o compensar una fuerza resistente o levantar un peso en condiciones más favorables.
En las denominadas máquinas compuestas, se combinan los beneficios de dos o más maquinas simples.
Las máquinas simples surgieron para resolver los problemas que planteaban las actividades cotidianas en tiempos muy remotos, entre ellas la caza, la pesca o el transporte de objetos pesados. En verdad primero se fueron diseñando ciertos utensilios, que después se fueron perfeccionando y es así como surgieron las primeras máquinas simples. Se podría decir que esas primeras máquinas funcionaron casi como una extensión de las manos humanas: fueron instrumentos de madera para cavar, rocas afiladas para cortar y otros. Pero sin duda, produjeron importantes cambios en la historia del hombre y en su relación con el trabajo.
Las máquinas simples comprenden aquellas que tienen un único punto de apoyo (lo que va variando entre ellas es la ubicación de dicho apoyo) y aprovechan algunos principios físicos básicos como momento de una fuerza, trabajo, potencia, energía y rendimiento mecánico. Se debe tener presente que las máquinas simples no escapan a la ley de la conservación de la energía: la energía no se crea ni se destruye en la máquina simple, solo se transforma.
Existen 6 máquinas simples
- Palanca
- Polea
- Plano inclinado
- Cuña
- Ruedas y ejes
- Tornillos
La palanca, una de las más importantes, es una barra rígida que puede girar alrededor de un punto fijo, el punto de apoyo. La fuerza que se aplica en la palanca recibe el nombre de fuerza motriz o potencia y la fuerza que se vence se conoce como resistencia. La longitud de la palanca es importante para vencer la resistencia.
La polea sirve para subir objetos pesados a cierta altura. Se trata de una rueda por la que por su parte externa pasa una cuerda; en uno de los extremos de dicha cuerda se coloca un peso o carga, que sube al aplicar una fuerza mayor al otro extremo. Sirve tanto para reducir la fuerza necesaria para elevar objetos como para cambiar la dirección. Existen poleas simples y otras formadas por varias ruedas; estas últimas reciben el nombre de aparejos.
En el plano inclinado lo que sucede es que la fuerza del peso se descompone en dos componentes. De este modo, el esfuerzo necesario para levantar la carga es menor.
La cuña es un cuerpo donde convergen dos planos inclinados algo afilados, se crea así un punto de contacto lacerante, que perite cortar o rasgar objetos sólidos.
La rueda es un cuerpo redondo que gira respecto de un punto fijo, denominado eje de giro, normalmente cilíndrico. Se usa para transmitir un movimiento giratorio entre ejes, facilitar el desplazamiento de objetos y personas, etc.
El tornillo no es más que un plano inclinado enroscado en espiral, a cada una de las vueltas se las llama rosca. Para que un tornillo entre en un cuerpo a través de su superficie se lo va haciendo girar, la fuerza que se necesita para dar cada vuelta y completar el proceso es siempre menor que la que se necesitaría para clavar hacerlo en una línea recta.
Ejemplos de máquinas simples
Muchísimos objetos de la vida cotidiana, que los usamos para viajar, para jugar o en el mundo del trabajo, se basan en una o más de estas seis máquinas tan conocidas. Se mencionan a continuación veinte máquinas simples a modo de ejemplo:
Norias: Permiten extraer agua mediante el principio fundamental del rosario hidráulico. Se coloca parcialmente sumergida y por medio del movimiento continuo habilita la extracción de agua.
Bombas de agua: Dispositivo que eleva, transfiere y comprime líquidos. Utiliza los principios fundamentales ligados a la presión.
Grúas: Mediante el efecto palanca consigue levantar peso por medio de una viga, realizando así menor cantidad de fuerza, manipulándola con poleas sobre un pivote giratorio que permite el movimiento horizontal. La estabilidad de la grúa la hace indispensable para el rubro de la construcción.
Tobogán: Utiliza los fundamentos de la máquina simple ‘plano inclinado’, donde se aprovecha la energía potencial, intervienen en él los conceptos de velocidad y aceleración, y se asume que no hay fuerza de fricción (o que esta es mínima).
Sube y baja: El efecto palanca se combina en este juego popular con el de plano inclinado, uniendo en una dos máquinas simples, y aprovechando a la vez el peso y la fuerza de gravedad, sobre la base de un punto de apoyo, ante la acción de la fuerza y la reacción de una resistencia.
Carretilla: Habitual en el área de la construcción, consiguiendo distribuir el peso orientándolo hacia la llanta, lo que hace que se pueda soportar un peso mucho mayor con el único esfuerzo de empujar la carretilla.
Engranaje: Rueda dentada que hace que un objeto pueda moverse más rápida o lentamente, por medio de la manipulación de la fuerza necesaria para moverlo.
Torno: Combinación de una manivela y un cilindro, lo cual permite levantar un cuerpo pesado por intermediación de una fuerza mucho menor.
Hacha: Esencial para separar o lacerar (leña, por ejemplo), lleva una pieza de metal terminada en forma de cuña, que es la que rasga y permite el corte.
Tijeras: Ejemplo típico de palanca sencilla, que combina la resistencia y la potencia para lograr su cometido, el de cortar al unir las dos cuchillas de acero.
Aljibe: Utiliza la polea para subir o bajar el balde, consiguiendo así elevar la masa de agua por medio de la transformación de energía.
Tornillo sinfín: Plano inclinado enroscado alrededor de una varilla, que cuando gira consigue introducir la rosca (un plano inclinado) en una madera, consiguiendo así mantener dos cosas unidas con mínimo esfuerzo.
Tenaza: Ejemplo de la palanca, de aplicación similar a la tijera.
Cascanueces: Palanca de combinación de potencia y resistencia, que permite aplicar la fuerza sobre el punto exacto para partir la nuez.
Caña de pescar: Utilizando el brazo humano como punto de apoyo, la palanca manipula la fuerza. El perfeccionamiento de las cañas de pesca fue haciendo cada vez menos trabajosa la tarea.
Balanza romana: Instrumento que mide masas, y que fundamentalmente se basa en palancas.
Guillotina: Máquina simple formada por una cuchilla muy afilada, hoy se emplea más que nada para cortar a la vez una cantidad grande de papeles.
Cuchillo: Aplica los mecanismos del plano inclinado logrando por medio del filo cortar, habitualmente comida o sogas.
Manivelas: Herramienta que se utiliza para transformar el movimiento rectilíneo en circular, o viceversa. Sirve para hacer girar un eje con menos esfuerzo (algo que era muy necesario en los coches antiguos).
Bicicleta: Aplica el fundamento de la rueda y eje para permitir el desplazamiento de la carga (la persona que va en la bicicleta).