LENGUAJE ALGEBRAICO Y SU VALOR EN LA DIVERSIDAD CULTURAL.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 3° - Matemáticas |
| Libro: | LENGUAJE ALGEBRAICO Y SU VALOR EN LA DIVERSIDAD CULTURAL. |
| Impreso por: | Invitado |
| Fecha: | jueves, 30 de enero de 2025, 23:33 |
1. Máximo Común Divisor de dos o más polinomios
Con lo que deberías de estar familiarizado antes de esta lección
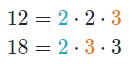
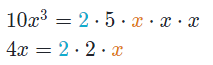
1.1. Máximo común divisor de expresiones algebraicas
2. Mínimo Común Múltiplo de dos o más polinomios
El mínimo común múltiplo (m.c.m) es el polinomio de menor grado que es múltiplo común de dos o más polinomios. Para hallar el m.c.m. de un grupo de polinomios se deben hallar todos sus factores, tomar cada uno de los factores con el mayor exponente con el que aparezca y multiplicarlos. Para hallar los factores de un polinomio es necesario factorizar.Ejemplo 1
Para hallar el m.c.m. de ![]() y
y ![]() , primero debemos encontrar los factores de cada uno de los polinomios.
, primero debemos encontrar los factores de cada uno de los polinomios.
Y los factores de
Entonces, podemos escribir:
Tomando cada uno de los factores con el mayor exponente con el que aparecen, tenemos que:
![]()
Realizando las multiplicaciones y reduciendo términos semejantes tenemos que:
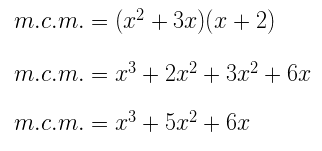
Minimo comum multiplo de polinomios
2.1. Mínimo común múltiplo de expresiones algebraicas
3. Fracciones algebraicas:
Fracciones algebraicas
Una fracción algebraica es el cociente de dos polinomios y se representa por:
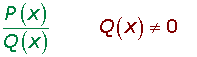
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.
Son fracciones algebraicas:
![]()
3.1. Propiedades aplicadas a las fracciones algebraicas
Fracciones algebraicas equivalentes
Dos fracciones algebraicas
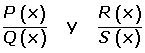
son equivalentes, y lo representamos por:
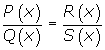
si se verifica que P(x) · S(x) = Q(x) · R(x).
![]()
son fracciones algebraicas equivalentes porque:
(x + 2) · (x − 2) = x2 − 4
Dada una fracción algebraica, si multiplicamos el numerador y el denominadorde dicha fracción por un mismo polinomio distinto de cero, la fracción algebraica resultante es equivalente a la dada.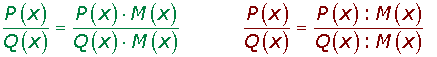
Simplificación de fracciones algebraicas
Para simplificar una fracción algebraica se divide el numerador y el denominador de la fracción por un polinomio que sea factor común de ambos.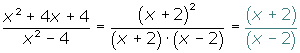
Amplificación de fracciones algebraicas
Para amplificar una fracción algebraica se multiplica el numerador y el denominador de la fracción por un polinomio.
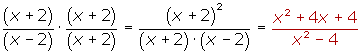
3.2. Operaciones con fracciones algebraicas: adición, sustracción, multiplicación y cociente.
Operaciones con fracciones algebraicas
Suma de fracciones algebraicas
Con el mismo denomiminador
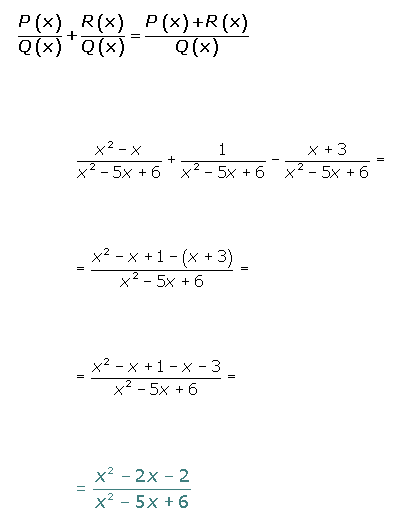
Suma de fracciones algebraicas
Con distinto denomiminador
En primer lugar se ponen las fracciones algebraicas a común denominador, posteriormente se suman los numeradores.
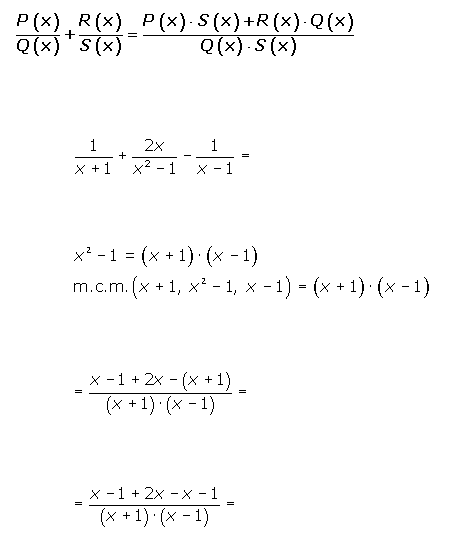
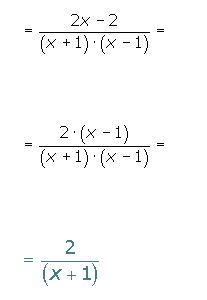
Suma de fracciones algebraicas
Multiplicación de fracciones algebraicas
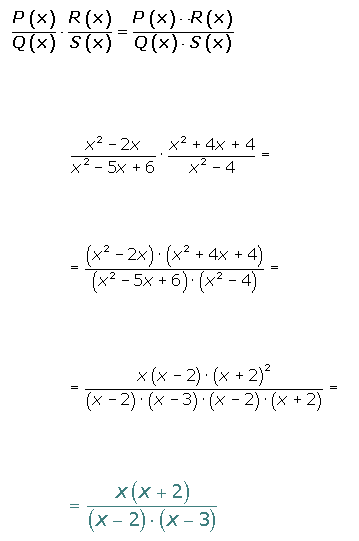
Multiplicación de fracciones algebraicas
División de fracciones algebraicas
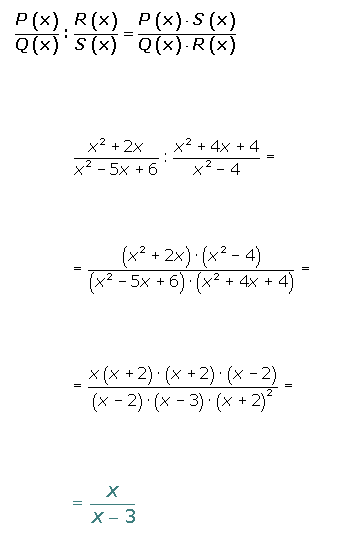
División de fracciones algebraicas
3.3. Operaciones combinadas de fracciones algebraicas.
Ya conoces cómo multiplicar y dividir fracciones algebraicas, pro es bueno que también conozcas que puedes encontrar en diferentes ejercicios ambas operaciones combinadas.
En el siguiente ejemplo te mostramos cómo operar en estos casos.
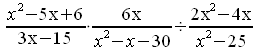
En esta expresión aparece la multiplicación y la división combinadas. Puedes proceder de tres formas:
1. Realizas la multiplicación y luego la división.
2. Realizas la división y luego la multiplicación.
3. Realizas ambas al mismo tiempo.
Te mostramos la tercera opción.
1. Hallas el recíproco de la tercera fracción:
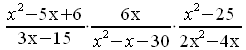
2. Factorizas los numeradores y denominadores que sean posibles:
![]()
3. Simplificas de forma cruzada o la misma fracción los factores que sean iguales:
![]()
4. Si al concluir la simplificación quedan productos indicados, debes efectuarlos para dar la respuesta final.
Operaciones combinadas fracciones algebraicas
OPERACIONES COMBINADAS CON FRACCIONES ALGEBRAICAS
4. Potenciación y radicación algebraica.
En esta temática se estudiará muy concienzudamente la expresión an conocida como la enésima potencia de a.
En esta temática se estudiará muy concienzudamente la expresión an conocida como la enésima potencia de a. ![]() El número a se conoce como la base y n como el exponente.
El número a se conoce como la base y n como el exponente.
Se iniciará el estudio de la expresión an en el caso donde a represente cualquier número real, es decir, a ∈ R y n un número entero positivo ( ![]() ), para este primer caso, la definición no presenta ninguna dificultad.
), para este primer caso, la definición no presenta ninguna dificultad.
El comportamiento de los exponentes en las operaciones con potencias está gobernado por ciertas reglas sencillas, pero se debe estar muy atento al aplicarlas con el fin de no caer en errores que van en contra de la definición.
PRODUCTO DE POTENCIAS DE IGUAL BASE.
Al efectuar productos de potencias de igual base se obtiene como resultado una potencia de igual base y como exponente la suma de los exponentes de las potencias involucradas, es decir: ![]() .
.
![]()
COCIENTE DE POTENCIAS DE IGUAL BASE.
Al efectuar cocientes de potencias de igual base se obtiene como resultado una potencia de igual base y como exponente la resta de los exponentes de las potencias
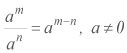
Comprobación para m > n:
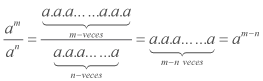
POTENCIA DE UNA POTENCIA.
Al elevar una potencia a una nueva potencia, se obtiene como resultado una potencia con la misma base, y como exponente el producto de los exponentes involucrados, es decir:
![]()
Comprobación:

POTENCIA CUYA BASE ES UN PRODUCTO.
Cuando se tiene una potencia cuya base es un producto de dos o más factores, se puede distribuir el exponente en cada una de los factores, es decir:
![]()
Comprobación:
![]()
Aplicando conmutativa y asociativa tantas veces como sea necesario.
POTENCIA CUYA BASE ES UN COCIENTE
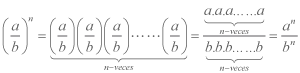
Cuando se tiene una potencia cuya base es un cociente de dos o más factores, se puede distribuir el exponente en cada una de los factores, es decir:
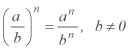
Comprobación:
Radicación
1. ![]() En esta igualdad cada expresión representa un número real, es decir se deben cumplir las condiciones adecuadas sobre n, a y b para que esto se cumpla.
En esta igualdad cada expresión representa un número real, es decir se deben cumplir las condiciones adecuadas sobre n, a y b para que esto se cumpla.
2. ![]() Como en el caso anterior en esta igualdad cada expresión representa un número real, es decir se deben cumplir las condiciones adecuadas sobre n, a y b para que esto se cumpla.
Como en el caso anterior en esta igualdad cada expresión representa un número real, es decir se deben cumplir las condiciones adecuadas sobre n, a y b para que esto se cumpla.
3. ![]() En esta propiedad si n es par a tiene que ser estrictamente mayor o igual cero, si n es impar no hay restricciones sobre a, es decir a ∈ R.
En esta propiedad si n es par a tiene que ser estrictamente mayor o igual cero, si n es impar no hay restricciones sobre a, es decir a ∈ R.
4. ![]()
4.1. Regla de los signos en la potenciación y radicación
Reglas de los Signos en la Potenciación
4.2. Propiedades de la potenciación y radicación.
PROPIEDADES DE LA POTENCIACIÓN

PROPIEDADES DE LA RADICACIÓN

5. Racionalización
1- Racionalización
Con frecuencia es necesario alterar la forma de una expresión con raíces para obtener otra expresión más simple. Esto se puede efectuar basándose en los conceptos de racionalización de fracciones con raíces y de amplificación de raíces de distinto índice.
Racionalizar una fracción consiste en encontrar una expresión equivalente que no tenga raíces en el denominador.
Para ello, se multiplica el numerador y el denominador por una expresión adecuada, de forma que permita expresar el denominador sin raíces.
Los casos más frecuentes de racionalización son:
a) Racionalizar fracciones que contengan una raíz cuadrada.
b) Racionalizar fracciones que contengan raíz enésima.
c) Racionalizar fracciones que contengan la suma o resta de dos o más raíces cuadradas o bien la suma o resta de un número natural con una raíz.
a) Racionalizar fracciones que contengan una raíz cuadrada en el denominador
Para racionalizar expresiones del tipo
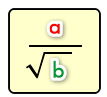
Se debe apmplificar la fracción por √b
Es decir:
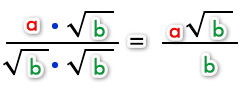
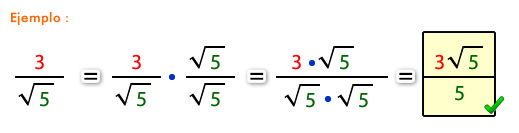
b) Racionalizar fracciones que contengan raíz enésima.
Racionalizar expresiones del tipo:
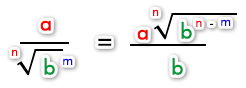
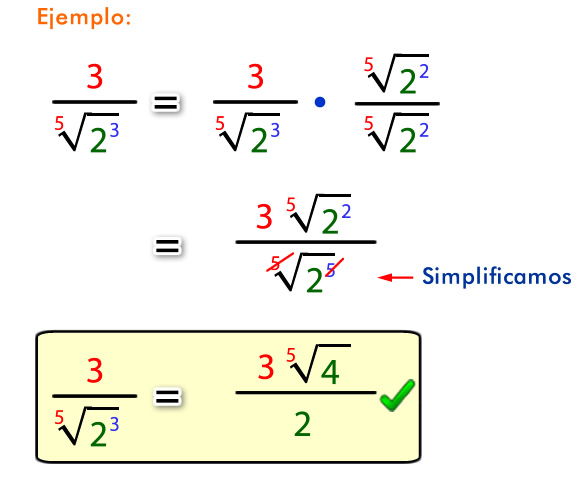
c) Racionalizar fracciones que contengan la suma o resta de dos o más raíces cuadradas o bien la suma o resta de un número natural con una raíz
Racionalizar expreciones del tipo:
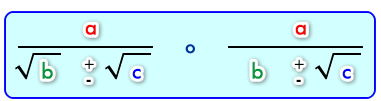
En general cuando el denominador sea un binomio con al menos un radical. Se multiplica el numerador y denominador por el conjugado del denominador. El conjugado de un binomio es igual al binomio con el signo central cambiado.
También tenemos que tener en cuenta que: "suma por diferencia es igual a diferencia de cuadrados".
(b ± c) (b ± c) = b2 - c2

5.1. Introducción a la racionalización