EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 2° - Matemáticas |
| Libro: | EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA. |
| Impreso por: | Invitado |
| Fecha: | jueves, 3 de abril de 2025, 04:59 |
Tabla de Contenidos
- 1. Monomios y las operaciones de adición, sustracción, multiplicación y división.
- 2. Potenciación y radicación de monomios.
- 3. Polinomios y las operaciones de adición, sustracción, multiplicación y división.
- 4. La regla de Ruffini y el teorema del resto.
- 5. Potenciación y radicación de polinomios
- 6. Operaciones algebraicas de polinomios
- 7. Productos notables y cocientes notables.
- 8. *Factorización y su aplicación en actividades de nuestro contexto
1. Monomios y las operaciones de adición, sustracción, multiplicación y división.
Suma de monomiosSólo podemos sumar monomios semejantes.
La suma de dos monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
axn + bxn = (a + b)bxn
2x2y3z + 3x2y3z = 5x2y3z
Si los monomios no son semejantes se obtiene un polinomio.
2x2 y3 + 3x2 y3 z
Producto de un número por un monomio
El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente de monomio por el número.
5 · 2x2 y3 z = 10x2 y3 z
Multiplicación de monomios
La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tenga la misma base, es decir, sumando los exponentes.
axn · bxm = (a · b)bxn +m
5x2 y3 z · 2 y2 z2 = 10 x2 y5 z3
División de monomiosSólo se pueden dividir monomios con la misma parte literal y con el grado del dividendo mayor o igual que el grado de la variable correspondiente del divisor.
La división de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene dividiendo las potencias que tenga la misma base, es decir, restando los exponentes.
axn : bxm = (a : b)bxn − m
![]()
Si el grado del divisor es mayor, obtenemos una fracción algebraica.
2. Potenciación y radicación de monomios.
Potenciacion de un monomio
Un monomio tiene una parte numérica y otra parte literal. Primero trabajaremos la parte numérica, es decir, aplicando la definición de potencia. Luego trabajaremos con la parte literal, en la cual multiplicaremos el exponente de cada letra por el exponente de la potencia dada.
Ejemplo: (3x2y)4, se nos pide elevar el monomio 3x2y a potencia 4
Tal como hemos dicho primero haremos la parte numérica: 34 = 3 x 3 x 3 x
3 = 81
Y ahora pasaremos a la parte literal: (x2y1)4 = x2x4y1x4 = x8y4
Finalmente la respuesta será: 81x8y4
Radicación de Monomios
En la radicación debemos trabajar por separado la parte numérica y la parte literal.
A la parte numérica le sacaremos la raíz correspondiente; y en la parte numérica dividiremos el exponente de cada letra entre el grado del radical
Ejemplo: √(16x4y6), se nos pide sacar la raíz cuadrada del monomio 16x4y6
Empezaremos por la parte numérica: √16 = 4
Ahora, en la parte literal: √x4y6 = x4÷2y6÷2 = x2y3 (el grado del radical es 2)
3. Polinomios y las operaciones de adición, sustracción, multiplicación y división.
En matemáticas, un polinomio es una expresión matemática constituida por un conjunto finito de variables (no determinadas o desconocidas) y constantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como también exponentes enteros positivos.
Las operaciones con polinomios se hacen de la siguiente forma:
- suma de polinomios: para sumar polinomios sumaremos los coeficientes de los términos del mismo grado (los demás los dejaremos igual). Los polinomios se pueden sumar y restar agrupando los términos y simplificando los monomios semejantes.
- resta de polinomios: para restar polinomios sumaremos al minuendo el opuesto del sustraendo, es decir, que cambiaremos de signo todos los monomios que hay en el sustraendo para así realizar una suma de polinomios.
- multiplicación de polinomios 1: realizaremos una multiplicación normal pero con polinomios. Para multiplicar polinomios se multiplica cada término de un polinomio por cada uno de los términos del otro polinomio y luego se simplifican los monomios semejantes.
- multiplicación de polinomios 2: multiplicaremos cada uno de los términos o monomios de un polinomio por cada uno de los términos del otro. Después, se sumarán los términos del mismo grado y los otros se dejarán igual.
Para decir de otra forma que es un polinomio podríamos decir que es una relación n-aria de monomios, o una sucesión de sumas y restas de potencias enteras de una o de varias variables indeterminadas.
Sumar polinomios implica combinar términos. Los términos semejantes son monomios que contienen la misma variable o variables elevadas a la misma potencia. Los siguientes son ejemplos de términos semejantes y no semejantes:
Todas estas operaciones con polinomios las entenderéis mucho mejor con el vídeo y además podréis practicarlas con nuestros ejercicios imprimibles con sus soluciones.
Suma, resta y multiplicación de polinomios
División de polinomios
Para realizar una división de polinomios haremos como si hiciéramos una división normal. A la izquierda colocaremos el dividendo y a la derecha el divisor. Entonces tendremos que dividir cada uno de los monomios del dividendo por cada uno de los monomios del divisor (en el vídeo lo entenderéis mejor con el ejemplo que os doy).
Además, si queréis practicar con divisiones de polinomios parecidas a la que os he explicado en la clase de hoy, podéis hacer los ejercicios imprimibles con sus soluciones
División de polinomios
4. La regla de Ruffini y el teorema del resto.
Con la regla de Ruffini, solamente se obtienen las soluciones enteras. Si la ecuación tiene soluciones complejas o reales, éste método no es válido.
Veremos que para obtener las soluciones de la ecuación, previamente hay que factorizar, por lo que con el mismo ejemplo explicaremos ambos conceptos.
Vamos a resolver un ejemplo explicando paso por paso.
Tenemos la siguiente ecuación:
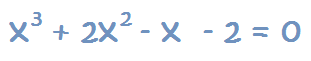
1 – Identificamos los coeficientes de cada término, que son los números que van delante de la incógnita. Para la ecuación anterior, los represento en verde para identificarlos:
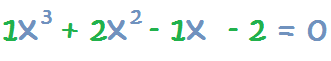
2 – Trazamos dos líneas perpendiculares de esta forma:

3 – Colocamos los coeficientes ordenados por su grado de mayor o menor:
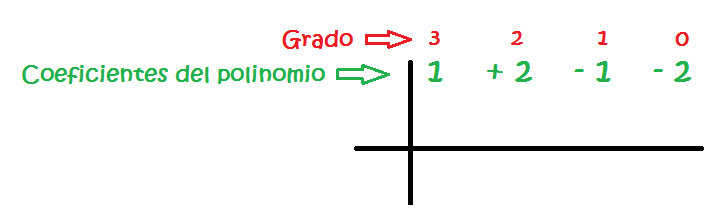
En la regla de Ruffini, el grado va disminuyendo de 1 en 1 y cada grado tiene su lugar. Por ejemplo si no tuviérmos ningún término que tenga x², en el lugar del grado 2, se colocaría un 0.
Los números que hemos escrito hasta ahora en el método de Ruffini, es equivalente a escribir la ecuación, es decir:

4 – Ahora escribimos un número a la izquierda de la línea vertical. Más adelante explicaremos qué número colocar aquí y por qué. De momento, empezamos con el 1.
Ese número corresponde al número (a) del binomio x – a:
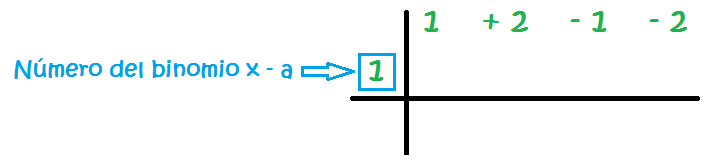
En este caso, escribir ahí un 1, significa el binomio (x – 1) en el método de Ruffini

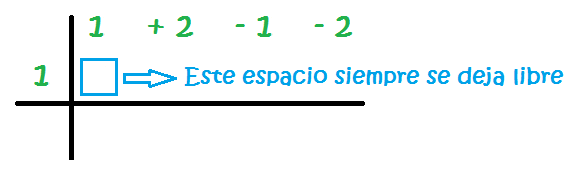
6 – Se hace la suma de la primera columna y el resultado de pone abajo:
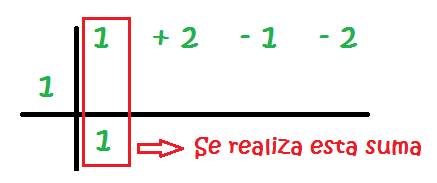
7 – Se multiplica el número de la izquierda por el resultado de la suma de la primera columna. El resultado se coloca en el hueco de la segunda columna:

8 – Se realiza la suma de la segunda columna:
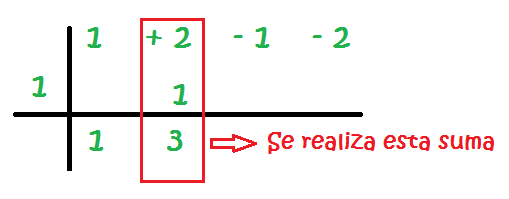
9 – Se multiplica el número de la izquierda por el resultado de la suma de la segunda columna. El resultado se coloca en el hueco de la tercera columna:
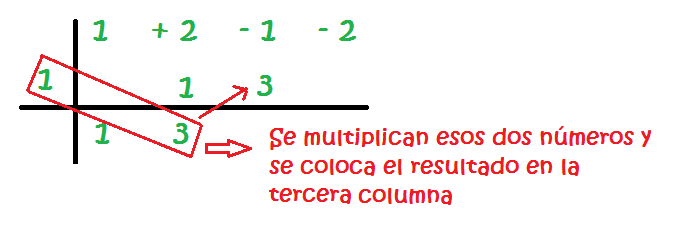
10 – Así sucesivamente hasta completar todas las columnas:
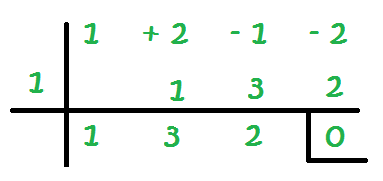
El objetivo es que en la última columna tengamos un 0. Esta es la explicación de qué número colocar a la izquierda de la línea:
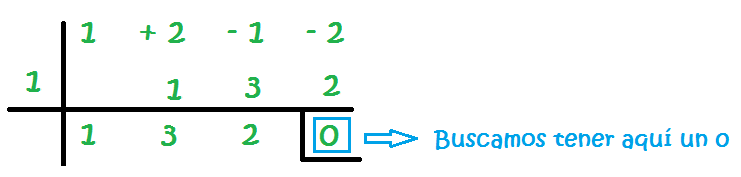
Si no tenemos un cero, tendríamos que probar con otro número a la izquierda de la línea vertical y reiniciar el proceso.
En el Curso de Polinomios, te enseño el método para que encuentres con facilidad el número para que resulte 0 en la última columna. Además de aprender como hacer Ruffini, tendrás más ejemplos del método de Ruffini y ejercicios explicados paso a paso.
Una vez hemos obtenido un cero al final, vamos a ver qué significa lo que tenemos hasta aquí:
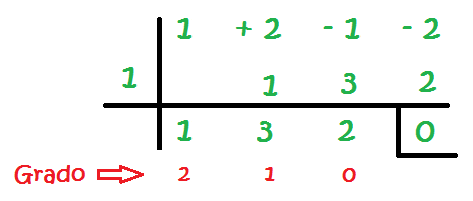
Lo que nos ha quedado en la última fila es otra ecuación, pero ahora, el número que está a la izquierda del 0, tiene grado 0 y éste va aumentando de 1 en 1 hacia la izquierda. En este caso, nos queda lo equivalente a tener esta ecuación:

Y como hemos visto antes, el 1 a la izquierda de la línea vertical significaba:

Lo que quiere decir que lo que tenemos hasta ahora es el producto de esas dos ecuaciones, que es igual a la ecuación original:
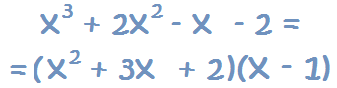
11 – Con la fila que nos ha quedado, volvemos a empezar. Empezamos probando con el 1:
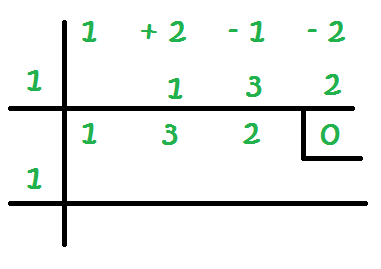
12 – Igual que antes, vamos multiplicando con el resultado de sumar en cada columna:
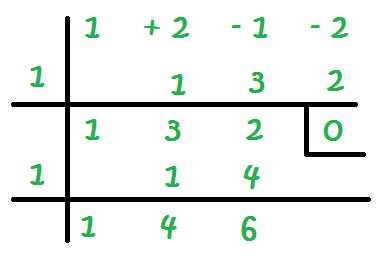
Al final tenemos un 6, y lo que queremos es tener un cero. Por tanto, debemos seguir probando, con -1, con 2, con -2… hasta encontrar el número que nos haga tener un cero en la última columna.
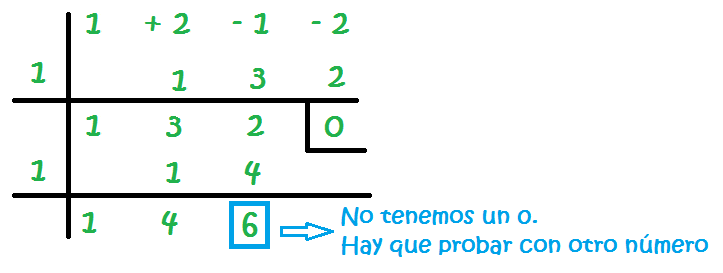
El número que nos hace tener un 0 al final es el -2:
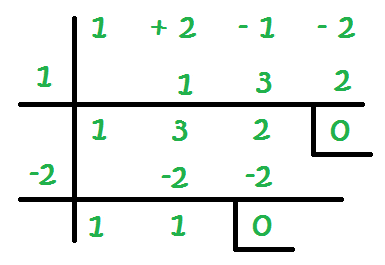
¿Y ahora que hacemos? ¿Cómo sabemos que hemos terminado?
El mayor grado de la última fila es 1, por tanto hemos terminado:
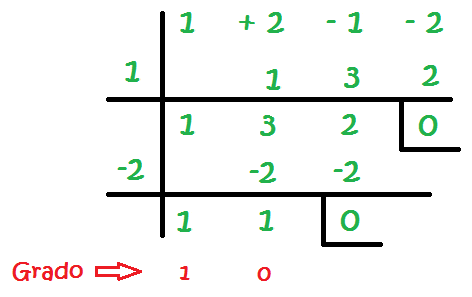
El resultado de la factorización de la ecuacuón por el método de Ruffini es el producto de la última fila y de los números que están a la izquierda de la línea vertical, pero expresados en forma de ecuación:

![]()
![]()
Por tanto, nuestra ecuación será:
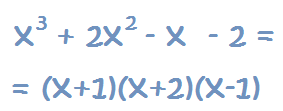
Hasta aquí hemos factorizado la ecuación. Ahora vamos a resolverla:
1 – Igualamos a 0, tal y como estaba en un principio
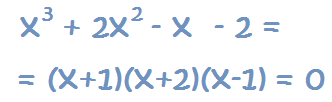
2 – Recuerda que cuando una multiplicación de dos o más factores tiene como resultado 0, quiere decir que uno de los factores es 0, ya que cualquier valor multiplicado por 0 es 0. Por tanto, cualquier factor podría ser 0.
Nos quedan tres ecuaciones de primer grado para despejar, de donde obtenemos las tres soluciones (ya que es una ecuación de tercer grado):
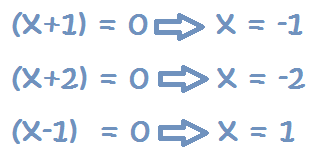
Soluciones: -1, -2 y 1
4.1. División por Ruffini - División de Polinomios
4.2. Teorema del Resto - Ejercicios Resueltos
4.3. Regla de Ruffini │ ejercicio 1
5. Potenciación y radicación de polinomios
Potencia de un polinomio
La potencia de un polinomio, P(x)n, es una forma abreviada de escribir el producto del polinomio n veces:
P ( x ) n = P ( x ) · P ( x ) · ... · P ( x ) ︸ n veces
Calculamos la potencia de un binomio (polinomio de dos términos).
(x + y)1 = x + y
(x + y)2 = (x + y) · (x + y) = x2 + 2xy + y2
(x + y)3 = (x + y) · (x + y)2 = x3 + 3x2y + 3xy2 + y3
Para apreciar las regularidades entre los coeficientes de las distintas potencias ordenamos los resultados.
Potencia | Resultado | Coeficientes |
(a + b)1 | a + b | 1 1 |
(a + b)2 | a2 + 2ab + b2 | 1 2 1 |
(a + b)3 | a3 + 3a2b + 3ab2 + b3 | 1 3 3 1 |
(a + b)4 | a4 + 4a3b + 6a2b2 + 4ab3 + b4 | 1 4 6 4 1 |
Nos fijamos en la regla que siguen los coeficientes de (a + b)4:
(a + b)4 = 1 · a4-0 · b0 + 4 · a4-1 · b1 + 6 · a4-2 · b2 + 4 · a4-3 · b3 + 1 · a4-4 · b4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
La relación existente entre los coeficientes de las distintas potencias de un binomio se conoce con el nombre de triángulo de Tartaglia.
Todas las filas comienzan y acaban con un 1, y los demás coeficientes se obtienen sumando los términos contiguos de la fila anterior.
Raíz cuadrada de un polinomio.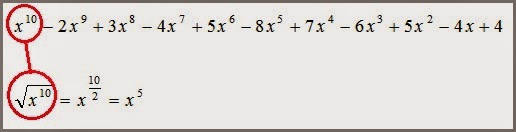



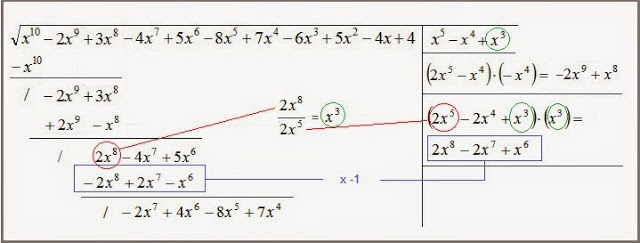
- A cada residuo obtenido se le añadirán tantos términos del polinomio subradical como sean necesarios para que el residuo resultante tenga un término más que el residuo de la operación anterior.
- Hemos de dividir siempre el primer término del residuo que se obtenga entre el doble del primer término de la raíz obtenida hasta el momento, que siempre claro está será el mismo. El cociente obtenido será siempre el siguiente término de la raíz.
- Crearemos siempre un polinomio con el doble de la raíz obtenida hasta el momento y el cociente obtenido del apartado anterior que al multiplicarlo por dicho cociente nos dará como resultado otro polinomio que se restará al residuo.

5.1. Propiedades de la potenciación | Potencia de un producto o multiplicación
6. Operaciones algebraicas de polinomios
Suma de polinomios
Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.
P(x) = 2x3 + 5x − 3
Q(x) = 4x − 3x2 + 2x3
1.Ordenamos los polinomios, si no lo están.Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2.Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3.Sumamos los monomios semejantes.
P(x) + Q(x) = 4x3− 3x2 + 9x − 3
Resta de polinomios
La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x− 4x − 3
P(x) − Q(x) = 3x2 + x − 3
Multiplicación de polinomiosMultiplicación de un número por un polinomio
Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número.
3 · ( 2x3 − 3 x2 + 4x − 2) = 6x3 − 9x2 + 12x − 6
Multiplicación de un monomio por un polinomio
Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.
3 x2 · (2x3 − 3x2 + 4x − 2) = 6x5 − 9x4 + 12x3 − 6x2
Multiplicación de polinomios
P(x) = 2x2 − 3 Q(x) = 2x3 − 3x2 + 4x
Se multiplica cada monomio del primer polinomio por todos los elementos segundo polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) =
= 4x5 − 6x4 + 8x3 − 6x3 + 9x2 − 12x =
Se suman los monomios del mismo grado.
= 4x5 − 6x4 + 2x3 + 9x2 − 12x
Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
También podemos multiplicar polinomios de siguiente modo:
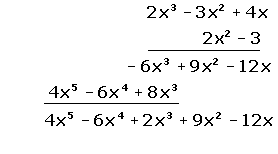
División de polinomios
Resolver la división de polinomios:
P(x) = x5 + 2x3 − x − 8 Q(x) = x2 − 2x + 1
P(x) : Q(x)
A la izquierda situamos el dividendo. Si el polinomio no es completodejamos huecos en los lugares que correspondan.
![]()
A la derecha situamos el divisor dentro de una caja.
Dividimos el primer monomio del dividendo entre el primer monomio del divisor.
x5 : x2 = x3
Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:
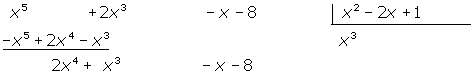
Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.
2x4 : x2 = 2 x2
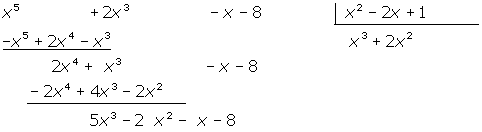
Procedemos igual que antes.
5x3 : x2 = 5 x
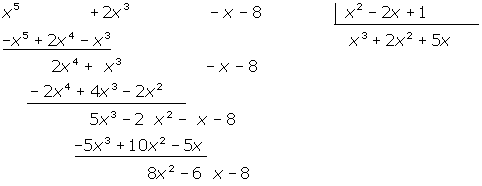
Volvemos a hacer las mismas operaciones.
8x2 : x2 = 8
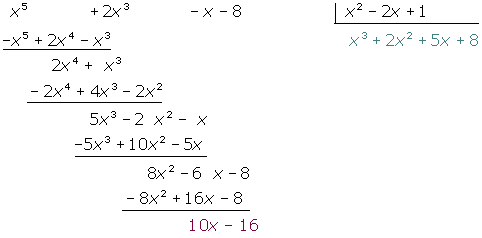
10x − 6 es el resto, porque su grado es menor que el del divisor y por tanto no se puede continuar dividiendo.
x3+2x2 +5x+8 es el cociente.
7. Productos notables y cocientes notables.
Productos notables
Los productos notables son multiplicaciones especiales que resultan de generalizar algunos productos.
Los productos notables nos permiten encontrar un resultado aplicando una formula general sin necesidad de desarrollar siempre los productos o potencias indicadas.
El cuadrado de lado (a+b),esta divido en cuatro regiones. Por tanto el área del cuadrado se puede representar como la suma de las áreas de las regiones que lo conforman. Es decir:
Binomio de suma al cuadradoUn binomio al cuadrado (suma) es igual es igual al cuadrado del primer término, más el doble producto del primero por el segundo más el cuadrado segundo.
(a + b)2 = a2 + 2 · a · b + b2
(x + 3)2 = x 2 + 2 · x ·3 + 3 2 = x 2 + 6 x + 9
Binomio de resta al cuadrado
Un binomio al cuadrado (resta) es igual es igual al cuadrado del primer término, menos el doble producto del primero por el segundo, más el cuadrado segundo.
(a − b)2 = a2 − 2 · a · b + b2
(2x − 3)2 = (2x)2 − 2 · 2x · 3 + 3 2 = 4x2 − 12 x + 9
Suma por diferenciaUna suma por diferencia es igual a diferencia de cuadrados.
(a + b) · (a − b) = a2 − b2
(2x + 5) · (2x - 5) = (2 x)2 − 52 = 4x2 − 25
Binomio al cuboBinomio de suma al cubo
Un binomio al cubo (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
(a + b)3 = a3 + 3 · a2 · b + 3 · a · b2 + b3
(x + 3)3 = x 3 + 3 · x2 · 3 + 3 · x· 32 + 33 =
= x 3 + 9x2 + 27x + 27
Binomio de resta al cuboUn binomio al cubo (resta) es igual al cubo del primero, menos el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, menos el cubo del segundo.
(a − b)3 = a3 − 3 · a2 · b + 3 · a · b2 − b3
(2x - 3)3 = (2x)3 - 3 · (2x)2 ·3 + 3 · 2x· 32 - 33 =
= 8x 3 - 36 x2 + 54 x - 27
Suma de cubosa3 + b3 = (a + b) · (a2 − ab + b2)
8x3 + 27 = (2x + 3) (4x2 - 6x + 9)
Diferencia de cubos
a3 − b3 = (a − b) · (a2 + ab + b2)
8x3 − 27 = (2x − 3) (4x2 + 6x + 9)
Producto de dos binomios que tienen un término común
(x + a) (x + b) = x2 + ( a + b) x + ab
(x + 2) (x + 3) =
= x2 + (2 + 3)x + 2 · 3 =
= x2 + 5x + 6
Cocientes notables
![]()
![]()
![]()
![]()
Más información https://ue.aprendiendomas.com.bo/pluginfile.php/294/mod_book/chapter/1583/Productos%20notables%20y%20cocientes%20notables.pdf
7.1. Productos Notables desde cero
7.2. Productos Notables, Cocientes Notables y División Algebraica
7.3. Cocientes Notables - Ejercicios Resueltos Nivel 1
7.4. Cocientes Notables - Ejercicios Resueltos Nivel 2
8. *Factorización y su aplicación en actividades de nuestro contexto
*