EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 2° - Matemáticas |
| Libro: | EL LENGUAJE MATEMÁTICO Y LA RELACIÓN CON LAS ACTIVIDADES DE LA VIDA COTIDIANA. |
| Impreso por: | Invitado |
| Fecha: | jueves, 21 de noviembre de 2024, 22:59 |
1. Nociones del lenguaje matemático y los fenómenos de la naturaleza.
En la naturaleza es común encontrar patrones matemáticos fascinantes. Las formas de algunas plantas, animales y entornos nos hacen preguntarnos si es posible que los propios organismos se diseñen de esta manera o si acaso hay una mente maestra detrás de su estructura. Y es que, desde cierta perspectiva, resulta increíble que el universo aparentemente caótico se organice con tanta precisión. Incluso, Albert Einstein preguntó alguna vez: “¿Cómo es posible que las matemáticas, producto del pensamiento humano, independiente de la experiencia, se ajusten excelentemente a los objetos de la realidad?”.
Para muchos las matemáticas son el lenguaje no sólo de la naturaleza, sino del universo. Sin embargo, es difícil afirmar esto sin provocar polémicas y dudas existenciales muy grandes, que ni siquiera la ciencia puede contestar aún. Pero no por ello dejaremos de pensar sobre la pregunta de Einstein y tratar de, por lo menos con nuevas preguntas, reflexionar más allá de lo aparente.
La utilidad de los fractales
Los fractales son objetos geométricos que mantienen la misma estructura básica en diferentes niveles. De esta manera, forman un patrón que hace que su desarrollo se mantenga regular. Algunos no nos parecen tan claros porque a primera vista son desordenados, pero están ahí. Las raíces de los árboles son un ejemplo de esto, pues crecen con la misma estructura, aunque no de la misma manera. Otros patrones son mucho más evidentes, como los encontrados en los copos de nieve.
Pero, ¿por qué hay fractales y patrones matemáticos en la naturaleza? En las primeras hojas de su libro Mathematics in Nature, John A. Adam propone algunas pistas exploradas por diversos matemáticos a lo largo de la historia.
Tiene sentido pensar que, si las condiciones del espacio son relativamente estables, obligan a las cosas a comportarse de forma estable también. A veces lentamente y a veces muy rápido, el universo está cambiando y nuestro planeta está cambiando también. Una prueba irrefutable de ello es la extinción de algunas especies de animales y plantas. Esto quiere decir que, para sobrevivir, los seres vivos se mantienen parecidos a sí mismos (como los fractales), en respuesta al entorno que habitan. Si este entorno cambiara drásticamente, es muy probable que dichos seres desaparezcan (dicho sea de paso, los seres humanos hemos modificado radicalmente el entorno que compartimos con otros seres vivos, y esto se ha visto reflejado en secuelas tan graves como el cambio climático).

Peter S. Stevens, autor de Patterns in Nature, explica que la forma en que se estructura la naturaleza responde a los límites impuestos por el espacio tridimensional que habitamos y a la relación entre el tamaño de las cosas y su funcionalidad. Esta idea podría estar ligada con una de Pat Murphy, que afirma que en la naturaleza los patrones responden a la necesidad de economizar energía y hacer su uso mucho más eficiente. Si una forma funciona para hacer sobrevivir a un organismo, se replica en múltiples niveles.
2. Nociones básicas de algebra
Saber mas https://ue.aprendiendomas.com.bo/pluginfile.php/293/mod_book/chapter/1566/algebra-basica.pdf
2.1. Estudio de Variables y Constantes
En matemáticas llamamos constante a una magnitud que no cambia con el paso del tiempo. En ocasiones, se puede tratar de un valor fijo y determinado.
Por otro lado, tenemos el concepto de variable, que se utiliza para definir toda cantidad susceptible de tomar distintos valores numéricos.
Para entender mejor la diferencia entre ambos conceptos, vamos a tomar como referencia la siguiente situación.
María y Rafa están haciendo un viaje por carretera, como están circulando por una autopista muy buena, han podido ir a 100km/h de velocidad durante la última media hora.
Como a lo largo del la última media de hora de viaje la velocidad ha sido la misma, podemos decir que, la velocidad del coche de María y Rafa ha sido una CONSTANTE.
Para que esto haya podido pasar el motor del coche ha tenido que ejercer distintas fuerzas de empuje, es decir en las bajadas el motor no ha necesitado empujar mucho para mantener los 100km/h, pero por contra, en las subidas, el motor ha tenido que empujar mucha más para que esa velocidad se mantuviera constante.
Esto quiere decir que la fuerza de empuje que ha hecho el motor del coche ha sido una VARIABLE, porque ha ido cambiando a lo largo del recorrido.
Después de esto te habrás dado cuenta que al ser así, la mayoría de las magnitudes o medidas que tomamos suelen ser variables, pero si lo piensas bien podrás encontrar algún constante más
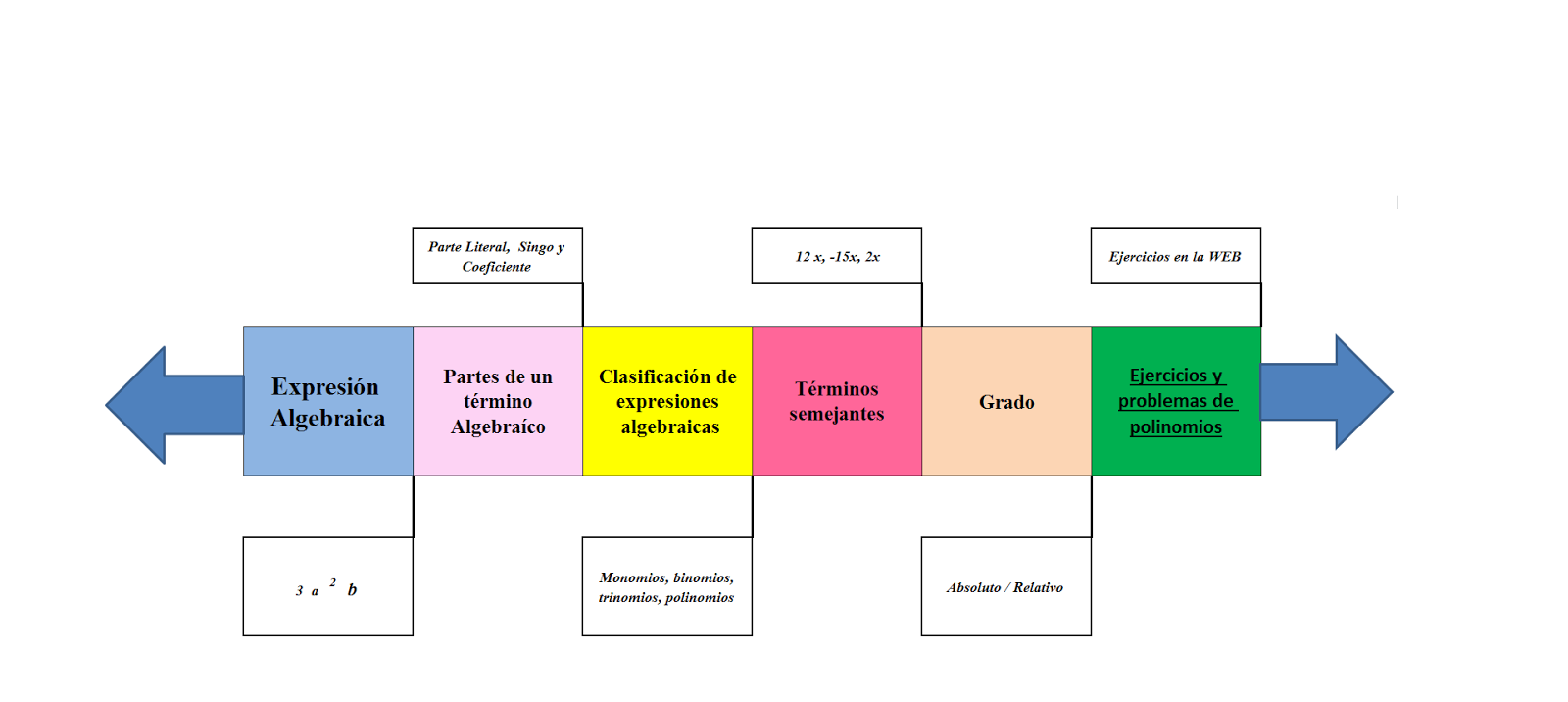
2.2. Grados de un término y un polinomio
Grado de un monomioEl grado de un monomio es la suma de todos los exponentes de las letras o variables.
El grado de 2x2 y3 z es: 2 + 3 + 1 = 6
Grado de un polinomio
El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.
Polinomio de grado cero
P(x) = 2
Polinomio de primer grado
P(x) = 3x + 2
Polinomio de segundo grado
P(x) = 2x2+ 3x + 2
Polinomio de tercer grado
P(x) = x3 - 2x2+ 3x + 2
Polinomio de cuarto grado
P(x) = x4 + x3 - 2x2+ 3x + 2
Grado de una ecuación
El grado de una ecuación es el mayor de los grados de los monomios que forman sus miembros.
5x + 3 = 2x +1 Ecuación de primer grado.
5x + 3 = 2x2 + x Ecuación de segundo grado.
5x3 + 3 = 2x +x2 Ecuación de tercer grado.
5x3 + 3 = 2x4 +1 Ecuación de cuarto grado.
2.3. Grado de un polinomio
2.4. Clases y Grados de un Polinomio | Aprende a identificarlos
2.5. Valor numérico
Valor numérico de una expresión algebraica
El valor númerico de una expresión algebraica, para un determinado valor, es el número que se obtiene al sustituir en ésta por valor numérico dado y realizar las operaciones indicadas.
L(r) = 2 r
r
r = 5 cm. L(5)= 2 · ![]() · 5 = 10
· 5 = 10![]() cm
cm
S(l) = l2
l = 5 cm A(5) = 52 = 25 cm2
V(a) = a3
a = 5 cm V(5) = 53 = 125 cm3
Valor numérico de un polinomioEl valor numérico de un polinomio es el resultado que obtenemos al sustituir la variable x por un número cualquiera.
P(x) = 2x3 + 5x - 3 ; x = 1
P(1) = 2 · 13 + 5 · 1 - 3 = 2 + 5 - 3 = 4
Q(x) = x4 − 2x3 + x2 + x − 1 ; x = 1
Q(1) = 14 − 2 · 13 + 1 2 + 1 − 1 = 1 − 2 + 1 + 1 − 1 = 0
R(x) = x10 − 1024 : x = −2
R(−2) = (−2)10 − 1024 = 1024 − 1024 = 0
2.6. Términos semejantes
Los términos semejantes son aquellos que tienen la misma parte literal, o dicho de otra forma aquellos que tengan las mismas letras y con igual exponente. Ejemplo: y son términos semejantes, además y también son términos semejantes, pues su parte literal es decir es la misma.En una expresión algebraica se llaman términos semejantes a todos aquellos términos que tienen igual factor literal ; es decir, a aquellos términos que tienen iguales letras (símbolos literales) eiguales exponentes.
Qué son terminos semejantes