TRIGONOMETRÍA, TECNOLOGÍA Y PRODUCCIÓN

Funciones trigonométricas de ángulos notables

En la actualidad para obtener el valor de una razón trigonométrica a partir de un ángulo dado, simplemente se utiliza una calculadora en la cual se introduce el valor del ángulo dado y se evalúa en la relación trigonométrica requerida. Los valores de estas razones también se pueden obtener utilizando triángulos rectángulos, cuyos ángulos serán a los que se les quiere encontrar sus razones trigonométricas. En ocasiones este método es muy engorroso, ya que para crear los triángulos se deben realizar bastantes operaciones. Sin embargo, existen ángulos en los que es muy fácil; a estos ángulos se les conoce como ángulos notables.

En las matemáticas y específicamente en la trigonometría, la palabra “notable” se utiliza para referirnos a procesos o valores que están bien definidos o muy comunes, y por ende, se reconocen y memorizan fácilmente. En este sentido, los ángulos notables son aquellos que tienen valores que aparecen muy seguido en la vida cotidiana. Estos ángulos son los de 30°, 45° y 60° y, en segundo lugar, los ángulos de 0°, 90°, 180°, 270° y 360°. Estos últimos, aunque no están definidos como 'notables', también son muy comunes.

Para los 3 ángulos notables podemos encontrar las razones trigonométricas —seno, coseno, tangente, cotangente, secante y cosecante— sin conocer las medidas exactas de los triángulos que los contienen, pues estos ángulos están contenidos en dos triángulos muy especiales e importantes en geometría, a saber: los triángulos isósceles rectángulos y los triángulos equiláteros.

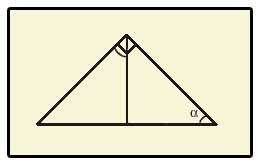
En geometría, un triángulo es un polígono de tres lados que se puede construir a partir de la unión de tres segmentos que se tocan en sus extremos. Cada uno de los puntos de unión entre dos segmentos se llama vértice y la abertura que hay entre cada par de segmentos se llama ángulo. Un triángulo tiene tres vértices y tres ángulos. Finalmente, una de las propiedades de los triángulos que nos interesa es que la suma de los ángulos de un triángulo es 180°.

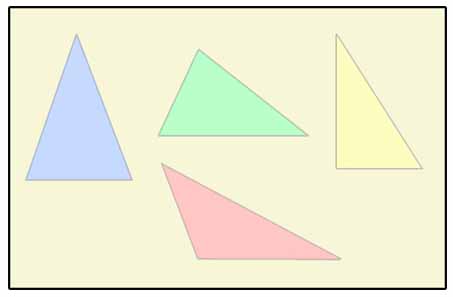
Existen varias formas para clasificar los triángulos.

• Una de ellas es a través de la amplitud de sus ángulos. Un triángulo es rectángulo cuando uno de sus ángulos es recto (es decir: mide 90°); dicho ángulo es delimitado por un par de lados que se conocen como catetos, mientras que el lado opuesto al ángulo recto recibe el nombre de hipotenusa. Un triángulo es acutángulo cuando sus tres ángulos interiores son agudos (miden menos de 90°) y obtusángulo cuando uno de sus ángulos es obtuso (mayor que 90°).
  
  
• Otra manera de clasificar los triángulos es por la longitud de sus lados. En esta clasificación, los triángulos son equiláteros cuando sus tres lados tienen la misma longitud; en este caso, los tres ángulos también son iguales. Un triángulo es isósceles cuando dos de sus lados tienen la misma longitud y de igual forma dos de sus ángulos son iguales. Finalmente se denominan escalenos aquellos triángulos cuyos tres lados tienen diferente longitud.

Obtención de las funciones trigonométricas para ángulos de 30° y 60°

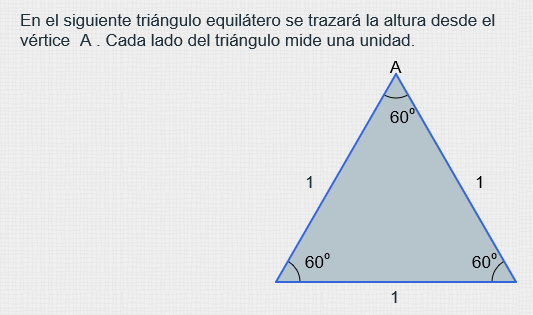
Antes de encontrar el valor para las funciones trigonométricas de los ángulos notables de 30° y 60°, vamos a originar dichos ángulos a partir de un triángulo equilátero. El triángulo equilátero que requerimos es aquel cuyos tres lados tienen una longitud de 1 unidad; además, cada uno de sus ángulos mide 60° (como siempre es el caso en un triángulo equilátero).

Ya que se tiene el triángulo equilátero, de éste se formarán dos triángulos a partir de su altura. Estos nuevos triángulos estarán compuestos por un ángulo de 30°

Y 60°. Finalmente para obtener el valor de una relación trigonométrica, ya sea para 30° o 60°

, sólo hay que utilizar sus definiciones.

En el siguiente recurso interactivo observa paso a paso la obtención de las razones trigonométricas para el ángulo de 60°. Nota además que de inmediato y de forma análoga se obtienen también las razones trigonométricas para el ángulo de 30°.

Obtención de las funciones trigonométricas para un ángulo de 45°

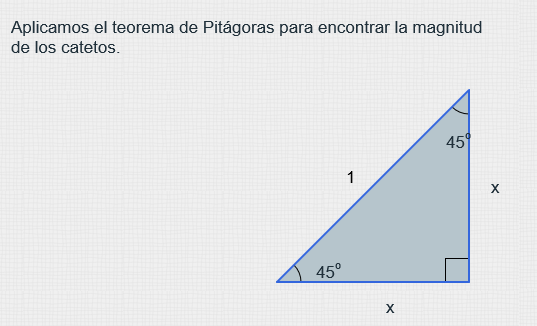
Para encontrar los valores de las funciones trigonométricas del ángulo notable de 45° utilizaremos un triángulo rectángulo isósceles. En dicho triángulo, se cumple que dos de sus lados tienen la misma longitud, digamos x

. Además, como el triángulo es rectángulo, uno de los ángulos es de 90°, por lo que los otros dos medirán 45° (recuerda que los triángulos isósceles siempre tienen dos ángulos idénticos).

Por conveniencia asignaremos a la hipotenusa el valor de 1

Unidad. A continuación podemos utilizar el teorema de Pitágoras para encontrar la longitud de sus catetos. Finalmente, para obtener el valor de las funciones trigonométricas solo hay que utilizar sus definiciones.

En el siguiente espacio interactivo observa paso a paso la obtención de las razones trigonométricas para el ángulo de 45°.

Múltiplos de ángulos notables

A partir de que ya obtuvimos los valores de las funciones trigonométricas de los ángulos notables de 30°, 45° y 60°, podemos obtener también los valores para funciones que representan los múltiplos de dichos ángulos. Para encontrar estas razones trigonométricas, vamos a utilizar los valores que ya hemos encontrado en un triángulo rectángulo.

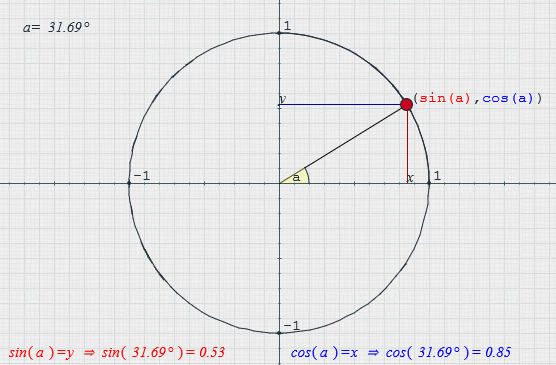
Estas definiciones las plantearemos tomando como base la circunferencia unitaria (es decir: ), una circunferencia de radio 1

Por lo que es útil recordar algunas definiciones:

El seno se define como la razón entre el valor de la coordenada Y del segmento que forma el ángulo con el eje X y la longitud de dicho segmento. En la circunferencia unitaria, el segmento es el radio y mide 1

Unidad, por lo que el seno es igual al valor de la coordenada Y:

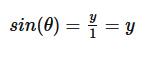
La relación inversa del seno es sin−1 y se define como:

El coseno es la razón entre el valor de la coordenada X del segmento que forma el ángulo con el eje X y la longitud del segmento. De igual forma que para el seno, como es una circunferencia unitaria, el coseno equivale a la coordenada X:

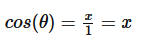
La relación inversa del coseno es cos−1 y se define como:

MÁS SOBRE FUNCIONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO