LEVANTAMIENTO DE DATOS ESTADÍSTICOS DE LAS ACTIVIDADES PRODUCTIVAS DEL CONTEXTO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 1° - Matemáticas |
| Libro: | LEVANTAMIENTO DE DATOS ESTADÍSTICOS DE LAS ACTIVIDADES PRODUCTIVAS DEL CONTEXTO |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 06:12 |
1. Recolección y organización de datos
2. Población, Muestra y Variables.
Es necesario que la población esté bien delimitada, y para ello hay que definirla en el tiempo y en el espacio. Gracias a esta limitación podremos determinar si algo forma parte o no de la población que estamos estudiando.
Población
Conjunto finito o infinito de elementos, sobre los que vamos a realizar observaciones.
Por ejemplo: los habitantes de un lugar, las piezas obtenidas de una máquina en un determinado tiempo, etc.
Como se puede extraer de la definición, la población como tal es un concepto muy abstracto, esto da lugar a que sea muy difícil o incluso imposible trabajar con ella al completo ya que puede ser un tamaño infinito o muy caro. A efectos prácticos, se estudia un subconjunto o muestra a partir de la cual extrapolamos los resultados al resto de la población. En general, cuanto mayor es la muestra mejores son los resultados que podemos obtener. Por ejemplo: si queremos analizar la resistencia de las piezas producidas por una máquina en un determinado periodo de tiempo es evidente que no podemos probar todas las piezas porque las vamos a dañar debemos seleccionar sólo una parte de ellas.
Las características que se tienen en cuenta son:
a) Tamaño: se establece mediante fórmulas en función del grado de confianza y precisión que planteemos.
b) Forma de elección: es fundamental para que la muestra sea representativa de la población de la cual se extrae.
Por ejemplo, si analizamos las piezas producidas por dos máquinas de forma simultánea e igual número, debemos obtener una muestra en la que ambas estén representadas en la misma proporción.
Muestra
Subconjunto finito de una población. El número de elementos que forman la muestra se denomina tamaño muestral.
Mas información https://ue.aprendiendomas.com.bo/pluginfile.php/132/mod_book/chapter/690/Ejercicios%20de%20estad%C3%ADstica.pdf2.1. Relación entre población y muestra
2.2. Tipos de variables estadísticas | Cuantitativas Cualitativas
3. Media, mediana y moda de un grupo de datos recolectados.
La mayor parte de las serie de datos muestran una clara tendencia a agruparse alrededor de un cierto punto central. Así pues, dada cualquier serie de datos particular, por lo general es posible seleccionar algún valor o promedio típico para describir toda la serie de datos. Este valor descriptivo típico es una medición de tendencia central o de ubicación.
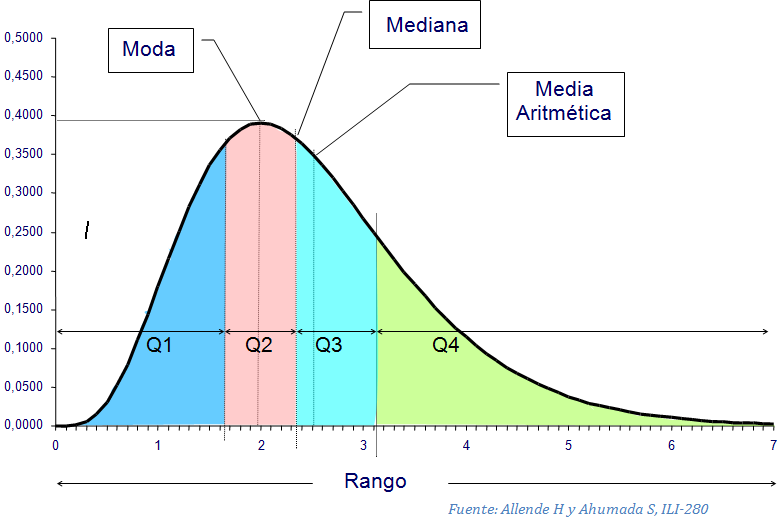
Cinco tipos de promedios a menudo usados como mediciones de tendencia central. Estos son la media aritmética, la mediana, la moda, el rango medio el eje medio.
La media aritmética
La media aritmética es el promedio o medición de tendencia central de uso más común. Se calcula sumando todas las observaciones de una serie de datos y luego dividiendo el total entre el número de elementos involucrados.
La expresión algebraica puede describirse como:
![]()
Para simplificar la notación se usa convencionalmente el término:
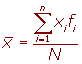
donde:
 = media aritmética de la muestra
= media aritmética de la muestra
= sumatoria de todos los valores de Xi
La mediana
La mediana es el valor medio de una secuencia ordenada de datos. Si no hay empates, la mitad de las observaciones serán menores y la otra mitad serán mayores. La mediana no se ve afectada por ninguna observación extrema de una serie de datos. Por tanto, siempre que esté presente una observación extrema es apropiado usar la mediana en vez de la media para describir una serie de datos.
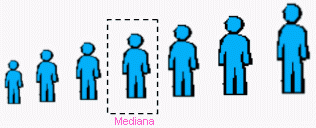
Para calcular la mediana de una serie de datos recolectados en su forma sin procesar, primero debemos poner los datos en una clasificación ordenada. Después usamos la fórmula de punto de posicionamiento:
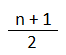
Para encontrar el lugar de la clasificación ordenada que corresponde al valor de la mediana, se sigue una de las dos reglas:
- Si el tamaño de la muestra es un número impar, la mediana se representa mediante el valor numérico correspondiente al punto de posicionamiento, la observación ordenada es (n+1)/2.
- Si el tamaño de la muestra es un número par entonces el punto de posicionamiento cae entre las dos observaciones medias de la clasificación ordenada. La mediana es el promedio de los valores numéricos correspondientes a estas dos observaciones medias.
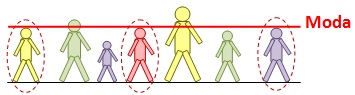
La moda o modo es el valor de una serie de datos que aparece con más frecuencia. Se obtiene fácilmente de una clasificación ordenada. A diferencia de la media aritmética, la moda no se ve afectada por la ocurrencia de los valores extremos.
Ejemplo: Los valores siguientes son las calificaciones de un alumno durante todo el año
7; 8; 9; 7; 9; 8; 8; 8; 7; 8
Podemos afirmar entonces que el modo es igual a 8, dado que es el valor que aparece con más frecuencia.
El rango medio
El rango medio es el promedio de las observaciones menores y mayores de una serie de datos.
El rango medio a menudo es usado como una medición de resumen tanto por analistas financieros como por reporteros meteorológicos, puesto que puede proporcionar una medición adecuada, rápida y simple para caracterizar toda una serie de datos, como por ejemplo todo una serie de lecturas registradas de temperatura por horas durante todo un día.
El eje medio
Como última medida de tendencia central, mencionamos al eje medio, que es el promedio del primer y tercer cuartiles de una serie de datos. Es decir:
Eje medio: (Q1 + Q2) / 2
Siendo Q1 y Q2, el primer y segundo cuartil. En conclusión podemos decir que es una medición de resumen usada para zanjar problemas potenciales introducidos por los valores extremos de los datos.
3.1. Media, mediana y moda | Datos agrupados en intervalos Ejemplo 1
3.2. Media mediana y moda | Datos sin agrupar
4. Representación gráfica e interpretación.
Cómo calcular el tamaño de muestra paso a paso en Excel
4.1. Calculo de Media, Mediana y Moda con excel