POLÍGONOS REGULARES E IRREGULARES EN EL ARTE Y LA TECNOLOGÍA DE LOS PUEBLOS
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 1° - Matemáticas |
| Libro: | POLÍGONOS REGULARES E IRREGULARES EN EL ARTE Y LA TECNOLOGÍA DE LOS PUEBLOS |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 07:21 |
1. Representación gráfica de las formas en los ejes cartesianos.
Ejes cartesianos y representación de puntos en el plan
Unos ejes cartesianos son un par de rectas reales perpendiculares que nos permiten identificar los distintos puntos del plano.
Identificaremos un punto P cualquiera mediante un par de números a y b, y escribiremos P =(a, b). Antes de ver cómo encontrar dichos a y b, analicemos un poco más a fondo los ejes cartesianos.
Esta es una representación gráfica de unos ejes cartesianos:
Observamos que tenemos dos rectas reales que se cruzan en el punto 0 de ambas.
Es destacable que dichas rectas dividen el plano en cuatro partes llamadas cuadrantes, y distinguidas según muestra la figuraLos distintos ejes tienen nombres propios:
- El eje horizontal es el eje de abscisas.
- El eje vertical es el eje de ordenadas.
El punto donde se cortan los dos ejes se llama origen (a veces sencillamente O), y tiene por coordenadas O=(0,0).
Una vez vista la notación habitual, ya estamos en condiciones de localizar puntos.
Una definición rigurosa de qué se considera coordenadas de un punto podría ser:
Dados uno ejes cartesianos y un punto P del plano, si a y b son el valor de la proyección del punto P sobre los ejes de abscisas y ordenadas respectivamente, entonces se tiene P=(a,b) .
Una definición más constructiva podría ser la siguiente:
Las coordenadas a y b de un punto P del plano, P=(a,b), son los puntos de intersección de las paralelas a los ejes de coordenadas trazadas desde el punto P con los ejes de coordenadas. La primera coordenada a es la intersección con el eje horizontal o de abscisas, y la segunda coordenada b es la intersección con el eje vertical o de ordenadas.
Un ejemplo visual resultará mucho más clarificador.
Ejemplo
De entrada, por situación inicial tenemos el punto y los ejes de coordenadas:
Si trazamos paralelas des del punto P, tenemos:
Y por tanto ya podemos decir que P= (2, -3).
El proceso de representar puntos es exactamente el mismo, pero a la inversa.
Supongamos que queremos representar el punto P= (-1, 2) en unos ejes cartesianos, el procedimiento a seguir es el siguiente:
Marcamos en el eje de abscisas el punto -1 y en el eje de ordenadas el punto 2:
Trazamos paralelas a los ejes de ordenadas y abscisas por los puntos a y b respectivamente:
La intersección de dichas paralelas es el punto P= (-1, 2)
1.1. El Plano Cartesiano y Ubicación de Puntos
1.2. Graficar puntos en el plano cartesiano
2. Perímetros y áreas en las formas
El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.
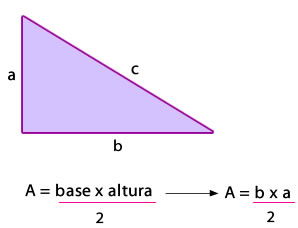
Área y perímetro del triángulo
- Cálculo del perímetro
P = a + b + c
Cálculo del área
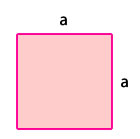
Área y perímetro del cuadrado
P = 4 • a
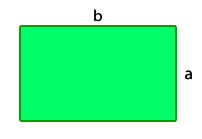
Área y perímetro del rectángulo
- Cálculo del perímetro
P = 2 • a + 2 • b
Área y perímetro del romboide
El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados.
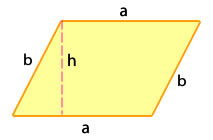
P = 2 • a + 2 • b
P = 2 • (a + b)
Cálculo del área
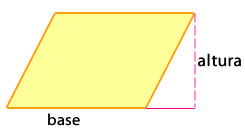
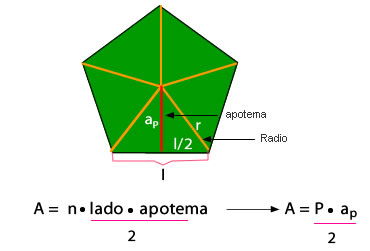

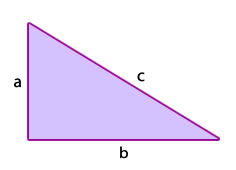
2.1. Perímetros de figuras regulares e irregulares
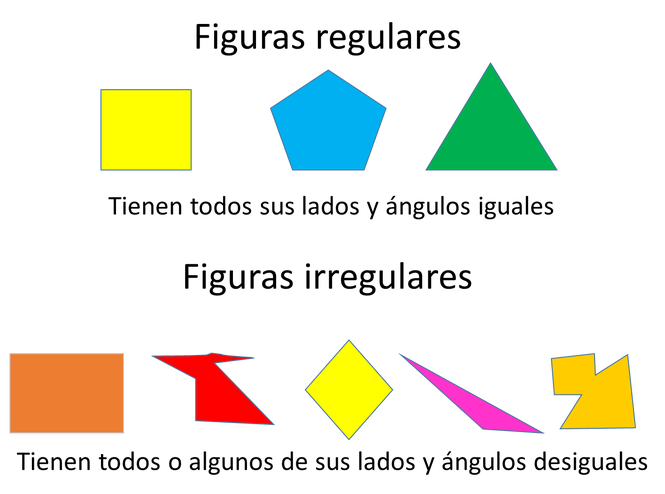
Existen figuras regulares que son las que tienen todos sus lados y sus ángulos iguales, y figuras irregulares que son las que no tienen todos sus lados y ángulos iguales.
En las figuras regulares el perímetro se puede obtener por medio de fórmulas como en los siguientes casos: triángulo equilátero, del cuadrado, del polígono regular, etc.
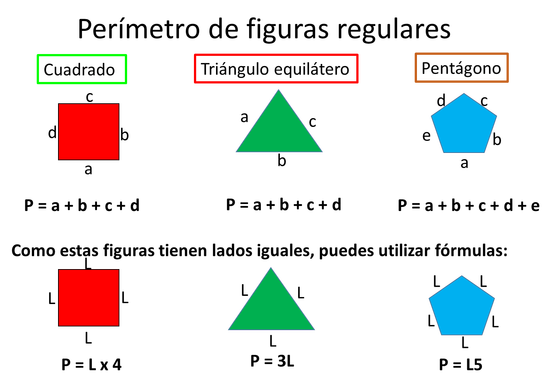
En cambio en las figuras irregulares, es necesario escribir en la fórmula los valores de sus lados uno por uno.

Cuando conoces la longitud del perímetro de cualquier figura, puedes darle el valor a cada uno de sus lados sabiendo que la suma de los valores de todos ellos, debe ser igual al perímetro dado.
Ejemplo: Si te dicen que el perímetro de un triángulo es igual a 15 cm, que obtengas la medida de cada uno de los lados del triángulo, lo primero que tienes que hacer es decidir qué tipo de triángulo será, y considerando las características de ese triángulo, dividir la longitud entre sus lados.
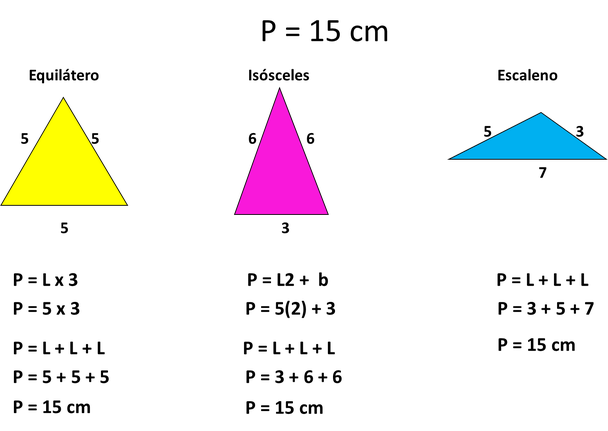
2.2. Áreas de figuras planas
2.3. Perímetro y Área de un círculo
3. Triángulos y su clasificación
Clasificación y propiedades de los triángulos
Clasificación de triángulos
Los triángulos se pueden clasificar según diferentes criterios:
- Por sus lados
- Por sus ángulos
Clasificación de triángulos según sus lados
Triángulo equilátero
Si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60 grados).
Triángulo isósceles
Si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.
Triángulo escaleno
Si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.
Clasificación de triángulos según sus ángulos
Triángulo Rectángulo
Si tiene un ángulo interior recto ( 90° ). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
Triángulo obtusángulo
Si uno de sus ángulos es obtuso (mayor de 90° ); los otros dos son agudos (menor de 90° ).
Triángulo acutángulo
Cuando sus tres ángulos son menores a 90° ; el triángulo equilátero es un caso particular de triángulo acutángulo.
Triángulo equiángulo
Normalmente se llama triángulo equilátero y ya se ha comentado anteriormente.
Propiedades de los triángulos
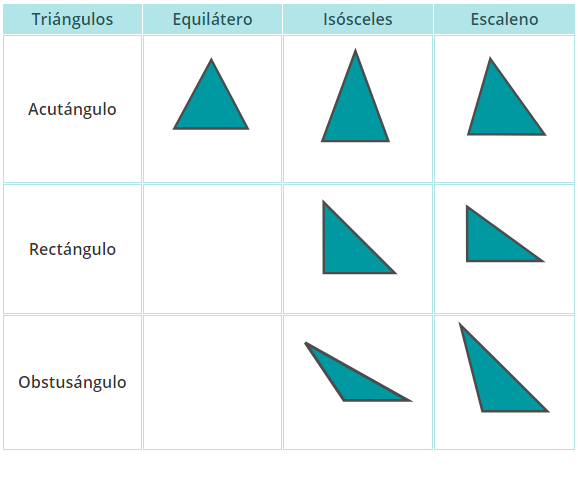
Podemos ver en el esquema anterior que las clasificaciones comentadas en el apartado anterior se pueden combinar de dos a dos (una de cada apartado).
Así, tenemos las siguientes características:
Triángulo acutángulo isósceles: con todos los ángulos agudos, siendo dos iguales, y el otro distinto, este triángulo es simétrico respecto de su altura diferente.
Triángulo acutángulo escaleno: con todos sus ángulos agudos y todos diferentes, no tiene ejes de simetría.
Los triángulos rectángulos pueden ser:
Triángulo rectángulo isósceles: con un angulo recto y dos agudos iguales (de cada uno), dos lados son iguales y el otro diferente, naturalmente los lados iguales son los catetos, y el diferente es la hipotenusa, es simétrico respecto a la altura que pasa por el ángulo recto hasta la hipotenusa.
Triángulo rectángulo escaleno: tiene un ángulo recto y todos sus lados y ángulos son diferentes.
Los triángulos obtusángulos son:
Triángulo obtusángulo isósceles: tiene un ángulo obtuso, y dos lados iguales que son los que parten del ángulo obtuso, el otro lado es mayor que estos dos.
Triángulo obtusángulo escaleno: tiene un ángulo obtuso y todos sus lados son diferentes.
3.1. Clasificación de los triángulos
4. Cuadriláteros
Cuadriláteros
Los cuadriláteros son un tipo especial de polígonos. Del mismo modo que los triángulos y otros polígonos, los cuadriláteros tienen propiedades especiales y pueden clasificarse por las características de sus ángulos y sus lados. Entender las propiedades de los distintos cuadriláteros te pueda ayudar a resolver problemas que contienen éste tipo de polígono.
Definiendo un cuadrilátero
Si analizamos su nombre “cuadrilátero” podemos entender a qué se refiere. El prefijo “cuad-” significa “cuatro,” y “latero” se deriva de la palabra Latina “lado.” Entonces un cuadrilátero es un polígono de cuatro lados.
Como es un polígono, sabemos que es una figura de dos dimensiones hecha de lados rectos. Un cuadrilátero tiene cuatro ángulos formados por sus cuatro lados. Abajo se muestran algunos ejemplos de cuadriláteros. Observa que cada figura tiene cuatro lados rectos y cuatro ángulos.
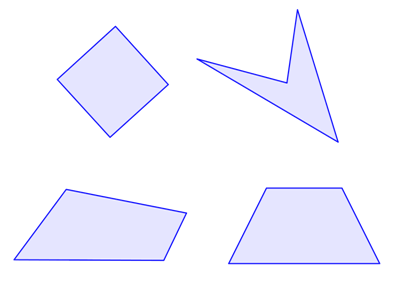
Los ángulos interiores de un cuadrilátero
La suma de los ángulos interiores de cualquier cuadrilátero es 360°. Considera los dos ejemplos siguientes.
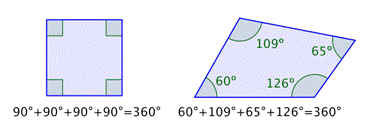
Podrías dibujar muchos cuadriláteros como estos y medir sus ángulos con cuidado. Encontrarás que para cada cuadrilátero, la suma de sus ángulos interiores siempre será 360°.
También puedes usar tu conocimiento de los triángulos como una forma de entender por qué la suma de los ángulos interiores de todos los cuadriláteros es 360°. Cualquier cuadrilátero puede dividirse en dos triángulos como se muestra en las figuras siguientes.
En la primera imagen, los cuadriláteros han sido divididos en dos triángulos. Se muestran las medidas de los ángulos de cada triángulo.
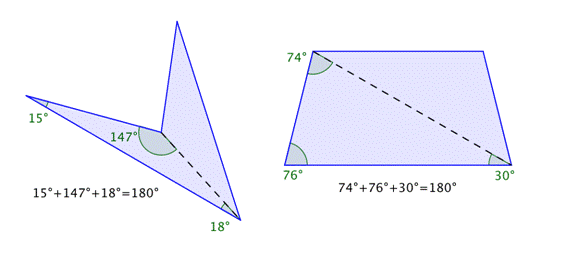
Estas medidas suman 180º. Ahora observa las medidas de los otros triángulos, también suman 180º

Como la suma de los ángulos interiores de cualquier triángulo es 180° y hay dos triángulos en un cuadrilátero, la suma de los ángulos de todos los cuadriláteros es 360°.
Tipos específicos de cuadriláteros
Empecemos por examinar el grupo de los cuadriláteros que tienen dos pares de lados paralelos. Estos cuadriláteros se llaman paralelogramos. Tienen una variedad de formas, pero un ejemplo clásico se muestra a continuación.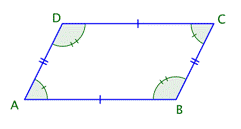
Imagina que extiendes los pares de lados opuestos. Nunca se van a intersectar porque son paralelos, Observa también, que los ángulos opuestos de un paralelogramo son congruentes, al igual que los lados opuestos. (Recuerda que “congruente” significa “del mismo tamaño.”) El símbolo geométrico para congruencia es ![]() , entonces puedes escribir
, entonces puedes escribir ![]() y
y ![]() . Los lados paralelos también tienen la misma longitud:
. Los lados paralelos también tienen la misma longitud: ![]() y
y ![]() . Estas relaciones son válidas para todos los paralelogramos.
. Estas relaciones son válidas para todos los paralelogramos.
Existen dos casos especiales de paralelogramos que te serán familiares de tus primeras experiencias con figuras geométricas. El primer caso especial se llama rectangulo. Por definición, un rectángulo es un paralelogramo porque sus pares de lados opuestos son paralelos, Un rectángulo también tiene la característica especial de que todos sus ángulos son rectos; los cuatro ángulos son congruentes.
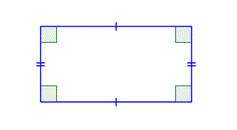
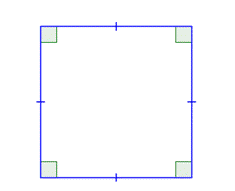
Un cuadrado es también un rectángulo porque tiene dos pares de lados paralelos y cuatro ángulos rectos. Un cuadrado también es un paralelogramo porque sus lados opuestos son paralelos. Entonces, un cuadrado puede clasificarse como cualquiera de las tres formas, siendo “paralelogramo” la descripción menos específica y “cuadrado,” la más descriptiva.
Otro cuadrilátero que podemos encontrar es el rombo. Los cuatro lados del rombo son congruentes, Sus propiedades incluyen que cada par de lados opuestos son paralelos, por lo que también es un paralelogramo.
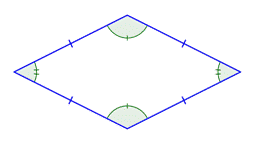
Resumiendo, todos los cuadrados son rectángulos, pero no todos los rectángulos son cuadrados. Todos los rectángulos son paralelogramos, pero no todos los paralelogramos son rectángulos. Y todas estas figuras son cuadriláteros.
El diagrama siguiente ilustra la relación entre los diferentes tipos de cuadriláteros.
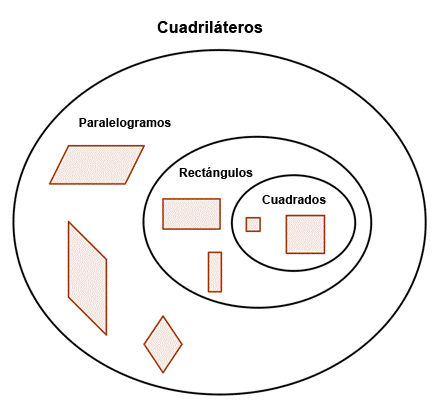
4.1. Clasificación de cuadriláteros y características
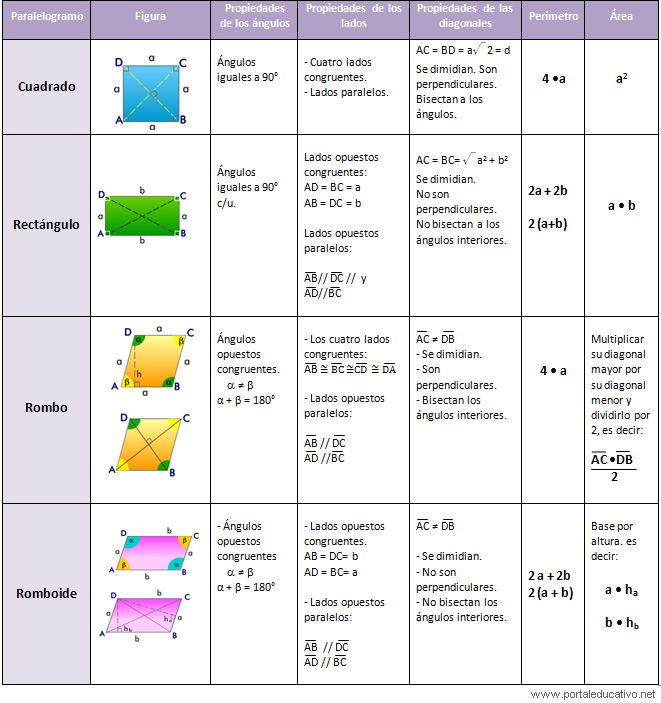
5. Paralelogramos: Cuadrado, Rectángulo y Rombo
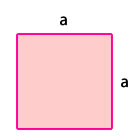
Cuadrado
Un polígono de 4 lados (una figura plana de lados rectos) donde todos los lados tienen igual longitud y todos los ángulos interiores son rectos (90°).
Tiene cuatro lados congruentes. Sus lados opuestos son paralelos. Las líneas diagonales que cruzan el cuadrado son perpendiculares. Las diagonales se dimidian (÷ en partes iguales)
- Diagonal: d = a√2
- Perímetro: p = 4a ·
- Área: A = a2
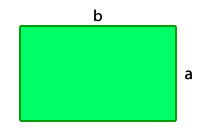
Rectángulo
Rectángulo es un paralelogramo de dos pares de lados de la misma medida y cuatro ángulos rectos. Las diagonales siempre son iguales y oblicuas.
El rectángulo a diferencia del cuadrado, no tiene todos sus lados de la misma longitud, solo tiene sus lados opuestos iguales.
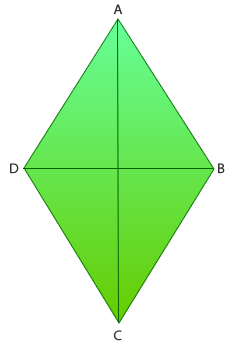
Es un paralelogramo de cuatro lados iguales, dos ángulos agudos (miden menos de 90°) y dos ángulos obtusos (miden más de 90°). Las diagonales del rombo son desiguales y perpendiculares.
Es un paralelogramo de dos pares de lados de la misma medida y dos ángulos agudos. No tiene ángulos rectos, todos son distintos a 90°. Sus diagonales son desiguales y oblicuas.
5.1. Trapecios: Isósceles, Escaleno y Recto
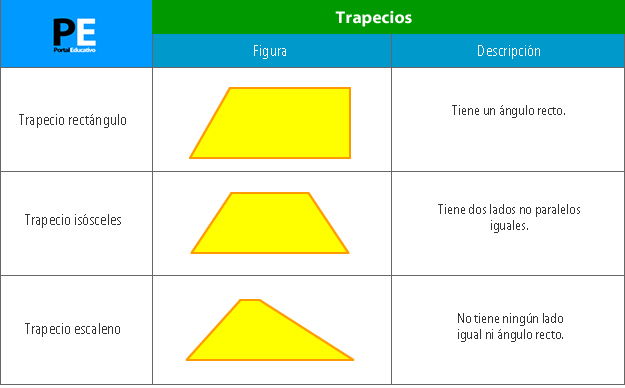
Propiedades Trapecio isósceles:
Además de las propiedades generales de los trapecios, los isósceles tienen las siguientes propiedades:
- Diagonales congruentes.
- Ángulos basales congruentes.
- Ángulos opuestos suplementarios.
Lado oblicuo del trapecio rectángulo
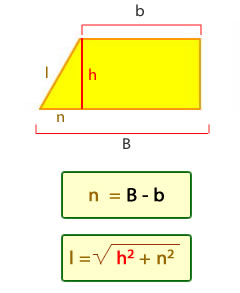
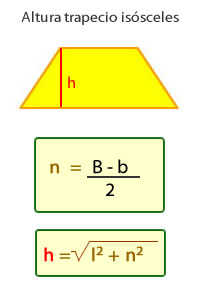
Altura del trapecio isósceles
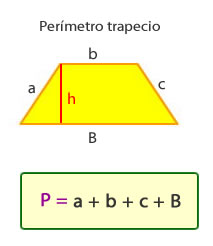
Perímetro del trapecio
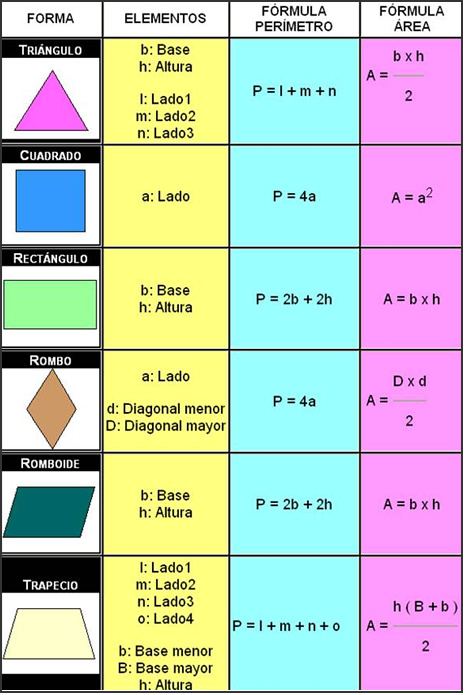
Área del trapecio
El área de un trapecio es la mitad del producto de la longitud de la altura por la suma de las longitudes de la bases.