IMPULSO Y CANTIDAD DE MOVIMIENTO EN EL DESARROLLO PRODUCTIVO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 5° - Ciencias Naturales: Física |
| Libro: | IMPULSO Y CANTIDAD DE MOVIMIENTO EN EL DESARROLLO PRODUCTIVO |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 07:44 |
1. Cantidad de movimiento en una colisión
CANTIDAD DE MOVIMIENTO
La cantidad de movimiento de una partícula se define como:
p = mv
La segunda ley de Newton establece que la
fuerza sobre un objeto es igual a la rapidez de cambio de la cantidad de
movimiento del objeto.En términos de la cantidad de movimiento, la
segunda ley de Newton se escribe como
F = dp/dt
La energía cinética de un cuerpo de masa m se puede expresar como:K = 1/2 mv2 =
p2/2m
Llamamos colisión a la interacción de dos
(o más) cuerpos mediante una fuerza impulsiva. Si m1 y m2 son las masas
de los cuerpos, entonces la conservación de la cantidad de movimiento
establece que:
m1v1i + m2v2i = m1v1f + m2v2f
Donde v1i, v2i, v1f , v2f son las velocidades iniciales y finales de las masas m1 y m2.
CLASIFICACIÓN DE LAS COLISIONES
Las colisiones se clasifican en:
Elásticas: cuando se conserva la energía cinética total.
Inelásticas: cuando parte de la energía cinética total se transforma en energía no recuperable (calor, deformación, sonido, etc.).
Perfectamente inelásticas: cuando los objetos permanecen juntos después de la colisión.
v1f=v2f
- COLISIONES PERFECTAMENTE INELÁSTICAS
Para colisiones perfectamente inelásticas se cumple lo siguiente:
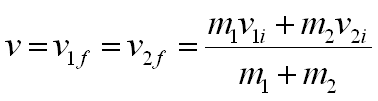
Si m2 está inicialmente en reposo, entonces:
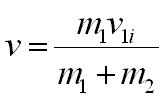
Si m1» m2, entonces v = v1i.
Si m1« m2, entonces v = 0.
Si v2i = -v1i , entonces:
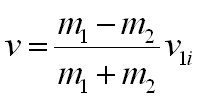
COLISIONES ELÁSTICAS
En colisiones elásticas se conserva el momento y la energía total. Entonces se tiene que:
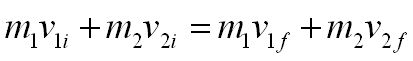
y
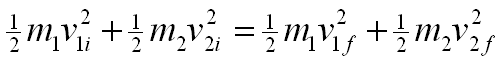
Es fácil mostrar, a partir de lo anterior, que:
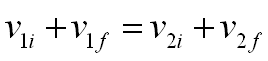
Si denotamos por u la velocidad relativa de los objetos, entonces:
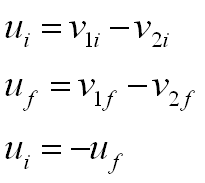
En una colisión elástica la velocidad relativa de los cuerpos en colisión cambia de signo, pero su magnitud permanece inalterada.
Es fácil mostrar que las velocidades finales de los dos objetos son:
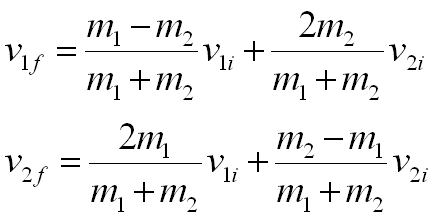
Si v2i = 0, entonces:
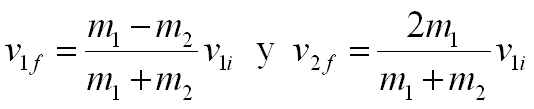
Si m1= m2, entonces v1f = 0 y v2f = v1f
Si m1 » m2, entonces v1f = v1i y v2f = v2i
Si m1« m2, entonces v1f = - v1i y v2f = (2m1/ m2) v2i
COLISIONES INELÁSTICAS
Las colisiones inelásticas se caracterizan por una pérdida en la energía cinética, podemos representar por e, la fracción de la velocidad relativa final entre la inicial, o sea:
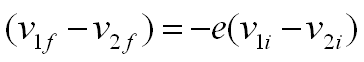
Donde e se conoce como el coeficiente de restitución. Para este caso las velocidades finales serán:
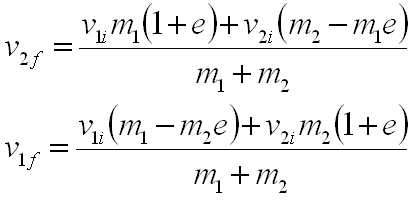
Si e = 0, se tiene el caso de colisiones perfectamente inelásticas, y si e = 1, entonces se tiene el caso de colisiones elásticas. Cualquier valor intermedio supone una pérdida de energía entre estos dos valores.
NOTA: RIEL DE AIRE
El Riel de Aire es un aparato de laboratorio utilizado para estudiar las coliciones en una dimensión. El riel consta de un tubo de sección transversal cuadrada con una serie de perforacoines por las que sale aire a presión. Sobre el riel se colocan carros que se deslizan sobre un colchon de aire que se forma entre el riel y el carro. Los carros se mueven en escencia sin fricción. Sobre los carros se colocan pesos para experimentar el choque de objetos de diferente masa.
El simulador de riel de aire permite modificar los parámetros más imoortantes: masas, velocidades iniciales y coeficiente de restitución, pudiendose llevar a cabo una gran variedad de experimentos con choque elásticos, no elásticos y perfectamente inelásticos.
Más información sobre colisiones ....
2. Impulso y conservación de la cantidad de movimiento
Impulso y cantidad de movimiento
- Impulso
El impulso es el producto entre una fuerza y el tiempo durante el cual está aplicada. Es una magnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo, por lo tanto si la fuerza es constante el impulso se calcula multiplicando la F por Δt, mientras que si no lo es se calcula integrando la fuerza entre los instantes de tiempo entre los que se quiera conocer el impulso.
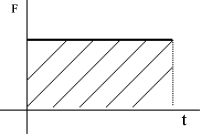
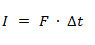
I = Impulso [kg·m/s]
F = Fuerza [N]
Δt = Intervalo de tiempo [s]
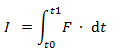
= Impulso [kg·m/s]
F = Fuerza [N]
t0, t1 = Intervalo de tiempo [s]
Unidad de impulso
El impulso se mide en kg·m/s, una unidad equivalente a N·s.
Cantidad de Movimiento
La cantidad de movimiento o momento lineal es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
- Cantidad de Movimiento
Cantidad de Movimiento
La cantidad de movimiento o momento lineal es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
![]()
Cantidad de Movimiento
p = Cantidad de movimiento [kg·m/s]
m = Masa [kg]
v = Velocidad [m/s]
Unidad de cantidad de movimiento
La cantidad de movimiento se mide en kg·m/s. Tiene la misma unidad que el impulso aunque sean conceptos diferentes.
Relación entre impulso y la cantidad de movimiento
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento, por lo tanto el impulso también puede calcularse como:
![]()
Relación entre impulso y cantidad de movimiento
I = Impulso [kg·m/s]
Δp = Variación de la cantidad de movimiento [kg·m/s]
Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de la masa:
![]()
Relación entre impulso y cantidad de movimiento
F = Fuerza [N]
Δt = Intervalo de tiempo [s]
Δp = Variación de la cantidad de movimiento [kg·m/s]
Más sobre impuslso y cantidad de movimiento lineal
3. Choque y colisión
Un choque físico o mecánico es percibido por una repentina aceleración o desaceleracion causada normalmente por un impacto, por ejemplo, de una gota de agua, aunque también una explosión causa choque; cualquier tipo de contacto directo entre dos cuerpos provoca un choque. Lo que mayormente lo caracteriza es la duración del contacto que, generalmente, es muy corta y es entonces cuando se transmite la mayor cantidad de energía entre los cuerpos.
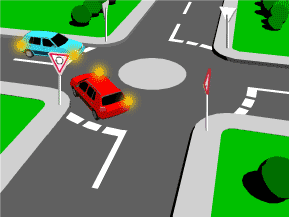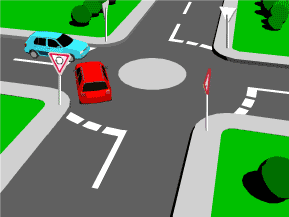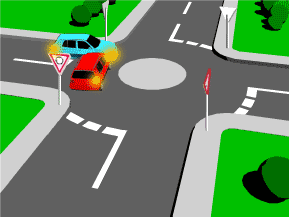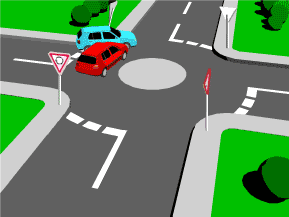
- Choque perfectamente elástico
que la energía cinética se conserve
conservación de la cantidad de movimiento
que no se presente deformación
También se conservan las formas de los cuerpos y no hay energía perdida por rozamiento, calor, etc. El coeficiente de restitución en este tipo de choques vale 1.
K = 1
Ec1(0) + Ec2(0) = Ec1(f) + Ec2(f)
K = Coeficiente de restitución
Ec1(0), Ec2(0) = Energía cinética inicial de los cuerpos 1 y 2
Ec1(f), Ec2(f) = Energía cinética final de los cuerpos 1 y 2
- Choque perfectamente inelástico
K = 0
- Choque semielástico
4. Colisiones elásticas en una dimensión.
Video y ejercicio de choque elástico en una dimensión
Más información..https://ue.aprendiendomas.com.bo/pluginfile.php/684/mod_book/chapter/3694/choque%20en%20una%20dimensi%C3%B3n.pdf
5. Colisiones inelásticas en la vida diaria
video de choque inelastico
6. Colisiones en dos o tres dimensiones
Choques en dos dimensiones
En un sistema aislado de dos patículas interactuantes, se conserva el momento lineal
El balance energético de la colisión se sustituye por el concepto de coeficente de restitución. Un diagrama en forma de tarta nos muestra como se transforma la energía inicial del sistema de dos partículas tras el choque
Se describe también el choque entre las dos partículas en un Sistema de Referencia que viaja con el centro de masa (c.m.). En un sistema aislado el c.m. se mueve con velocidad constante. El lector puede así comparar las descripciones de un mismo fenómeno desde dos puntos de vista diferentes
El objetivo es estudiar los choques bidimensionales de dos partículas en el Sistema de Referencia del Laboratorio (Sistema-L) y en el Sistema de Referencia del Centro de Masas (Sistema–C).
Sistema de Referencia del Laboratorio
Supongamos que chocan dos discos o esferas de masas m1 y m2 y radios r1 y r2.
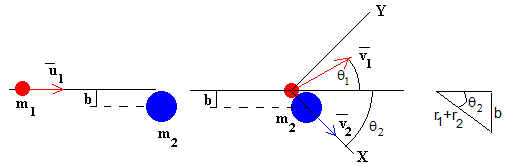
Choque ó colisión en dos dimensiones