APLICACIÓN DE LA ENERGÍA EN LOS PROCESOS PRODUCTIVOS
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 5° - Ciencias Naturales: Física |
| Libro: | APLICACIÓN DE LA ENERGÍA EN LOS PROCESOS PRODUCTIVOS |
| Impreso por: | Invitado |
| Fecha: | domingo, 24 de noviembre de 2024, 13:40 |
Tabla de Contenidos
- 1. Trabajo realizado por una fuerza constante y fuerza variable.
- 2. Trabajo y su relación con la energía cinética
- 3. Aplicación de la potencia mecánica en la industria y la tecnología
- 4. Energía potencial mecánica y energía potencial elástica
- 5. Aplicación de la Ley de Conservación de la Energía en las energías alternativa
1. Trabajo realizado por una fuerza constante y fuerza variable.
Trabajo de una fuerza constante
Cuando una fuerza constante se aplica sobre un cuerpo que realiza un desplazamiento Δx en la dirección de la fuerza aplicada, se dice que la fuerza realiza un trabajo
Vemos que las unidades en las que se mide el trabajo son las de una fuerza por una distancia, siendo la unidad SI 1 julio = 1 newton·m.
El trabajo es positivo si la fuerza se aplica en el mismo sentido que se realiza el desplazamiento y negativo si se opone a él. El trabajo es nulo si no hay desplazamiento. Una persona puede ejercer toda la fuerza que quiera contra una pared, hasta agotarse. Si la pared no se mueve, no ha realizado trabajo alguno.
Si la fuerza, como vector que es, posee una dirección diferente al desplazamiento, solo su componente en la dirección de este realiza trabajo.
Esta cantidad de expresa de manera más sencilla con ayuda del producto escalar
Vemos que
El trabajo es una cantidad escalar, con signo.
No se realiza trabajo si se ejerce una fuerza pero no se produce desplazamiento.
Una fuerza perpendicular al desplazamiento no realiza trabajo alguno.
Trabajo de una fuerza variable
Si tenemos una partícula que realiza una trayectoria arbitraria, sometida a una fuerza variable con la posición o el tiempo, podemos hallar el trabajo dividiendo el camino en diferenciales casi rectilíneos, calculando el trabajo (diferencial) en cada uno, y sumando (integrando) el resultado.
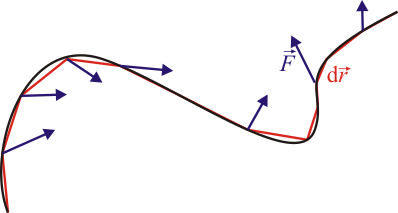
El trabajo diferencial es igual a
A partir de aquí obtenemos el trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C como la suma de los trabajos elementales a lo largo de dicha curva.
Respecto a la notación, el hecho de que el trabajo diferencial (que no diferencial de trabajo) se represente como δW en lugar de dW se debe justamente al hecho de que es una cantidad que depende del camino, como se estudia en más detalle en Termodinámica.
Ver mas sobre trabajo realizado sobre una fuerza variable
2. Trabajo y su relación con la energía cinética
Trabajo y energía cinética
Vamos a tratar en este artículo el concepto de trabajo y su relación con la energía cinética, mencionada ya en el artículo sobre energía mecánica.
La noción de energía es uno de los conceptos mas básicos en física y en efecto en todas las ciencias. La energía puede tomar muchas formas pero la forma particular que nos interesa en este artículo es la energía contenida en un cuerpo debido a su movimiento, la energía cinética. El trabajo (como concepto físico) hecho sobre un cuerpo implica que una fuerza actúe en él durante un desplazamiento. Veremos como la energía cinética de un cuerpo cambia cuando sobre él se realiza un trabajo lo que se conoce como teorema trabajo-energía, y como estos resultados nos pueden permitir entender diversos aspectos del movimiento y resolver problemas que pueden ser dificultosos de resolver utilizando la segunda ley de Newton directamente. Una vez que hayamos aprendido a calcular el trabajo, tendremos una poderosa herramienta para la comprensión del movimiento.
La energía cinética y las fuerzas constantes
La solución de las ecuaciones de movimiento partiendo de la segunda ley de Newton, F = ma, dan la posición del vector desplazamiento como función del tiempo, sin embargo tales soluciones pueden ser difíciles. Existe una vía para encontrar las soluciones a las ecuaciones de movimiento donde se puede esquivar el problema de cómo la posición del cuerpo varía con el tiempo. Con este nuevo enfoque podemos relacionar el desplazamiento de un cuerpo sometido a una fuerza con su rapidez*.
En el artículo sobre movimiento rectilíneo llegamos a las expresiones de cálculo del desplazamiento y la velocidad de un cuerpo que se mueve bajo la acción de una fuerza constante, las que pueden exponerse como:
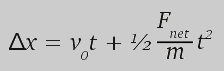(ecuación 1)
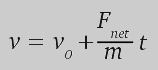(ecuación 2)
El desplazamiento Δx es x - x0 , donde la posición x varía con el tiempo y x0 es la posición al tiempo t = 0. Para eliminar el tiempo, lo despejamos en la ecuación 2 y los sustituimos en la ecuación 1. Cancelando los términos iguales y reorganizando podemos llegar a que:
Fnet
Δx = ½mv2 - ½mv02 (ecuación 3)
Esta expresión es todo lo que necesitamos para saber cuan rápido se mueve un cuerpo en el que actúa una fuerza neta constante después de haber viajado una distancia.
La cantidad de la izquierda de la ecuación 3 es el trabajo neto, wnet, hecho por la fuerza neta sobre el cuerpo, de forma que para una fuerza constante en una dimensión:
wnet = Fnet Δx (ecuación 4)
De esta forma podemos definir con palabras el concepto de trabajo:
Como el producto de la magnitud de la fuerza neta aplicada a un cuerpo por el desplazamiento que realiza el cuerpo.
Por su parte el término de la derecha de la ecuación 3 representa el cambio de la energía cinética contenida en el cuerpo debido al trabajo aplicado, ya que como sabemos del artículo energía mecánica:
Ec = ½mv2 (ecuación
5)
La energía cinética es un escalar no negativo y depende solamente de la magnitud de la velocidad, es decir de la rapidez.
El trabajo es un concepto tan importante que se ha reservado un nombre especial para su unidad, el joule en honor a James Joule que desarrolló importantes trabajos en este campo.
Un joule (J), es el trabajo realizado por una fuerza de 1N cuando ha movido un cuerpo una distancia de 1m. La ecuación 3 nos indica que dada la igualdad, la energía cinética (al igual que cualquier otra forma de la energía) también se pueden medir en joules. Si se fija, por definición el trabajo nos queda en N·m, mientras la energía cinética está en kg·m2/s2. No es difícil demostrar que 1N·m = 1kg·m2/s2.
En el lenguaje coloquial la palabra trabajo tiene diferentes significados, no se puede confundir la connotación coloquial con la definición precisa dada por la ecuación 4. Muchas veces en la vida diaria la palabra trabajo se usa en concordancia con la definición científica, estamos de acuerdo que para arrastrar una caja por el piso tenemos que hacer un trabajo. En este caso hay plena concordancia, se hace una fuerza y se produce un desplazamiento. Pero también acostumbramos a llamar trabajo al que hacemos cuando sostenemos estacionario un objeto en los brazos tal como una bolsa de mercado, aquí no hay trabajo ya que no hay desplazamiento.
El teorema trabajo-energía
Miremos de nuevo a la ecuación 3. Suponga que un cuerpo se mueve bajo la influencia de una fuerza neta constante, desde una posición inicial xi a una posición final xf , es decir, tiene un desplazamiento Δx = xf - xi . Como cambia su rapidez lo hace también su energía cinética. El cambio de la energía cinética, ΔEc, está dado por:
ΔEc
= Ecf - Eci
(ecuación 6)
Observe que el término de la derecha de la ecuación 6 corresponde plenamente con el de la ecuación 3, por lo que:
Wnet = ΔEc
(ecuación 7)
La ecuación 7 se conoce como el teorema trabajo-energía, que se podía enunciar como:
"Cuando sobre un cuerpo se realiza trabajo, se produce un cambio de igual magnitud en su energía cinética."
Como sabemos, el trabajo es el producto de dos magnitudes
vectoriales, fuerza y desplazamiento, de esto se desprende que el trabajo
también será vectorial, pero como estamos trabajando en un sistema
uni-direccional, tanto la fuerza neta como el desplazamiento quedan
completamente definidos asignándoles un signo, de esta forma, el trabajo se
considera positivo cuando la fuerza neta está en la misma dirección que el
desplazamiento y de signo negativo cuando la fuerza neta está en la dirección
contraria al desplazamiento. Lo que significa, en términos de la energía
cinética, que cuando el trabajo es positivo, aumenta la energía cinética del
cuerpo y cuando es negativo la reduce.
Supongamos que lanzamos una piedra hacia arriba. Mientras la piedra sube, el
signo del desplazamiento es contrario a la fuerza de la gravedad
que está actuando en ella (el desplazamiento es hacia arriba y la gravedad es
hacia abajo), se está realizando trabajo negativo sobre la piedra, y de acuerdo
al teorema trabajo-energía, la energía cinética de la piedra está bajando. Una
vez que alcanza la altura máxima la piedra se detiene, ha perdido toda su
energía cinética (v = 0), comienza entonces el descenso, ahora el
trabajo es positivo (la gravedad y el desplazamiento son en la misma dirección)
y la energía cinética vuelve a subir gradualmente hasta llegar a ser del valor
inicial, cuando la piedra llegue al punto de partida (estamos considerando que
no hay pérdidas de energía por rozamiento con el aire).
Pero, sorpresivamente al llegar al punto de partida el trabajo neto es cero, no
se ha hecho trabajo neto sobre la piedra, ya que el desplazamiento final es
también cero. No es difícil darse cuenta que los signos positivo y negativo de
trabajos iguales de ida y de vuelta hacen que se anulen mutuamente.
El teorema trabajo-energía es útil en realidad si podemos calcular el trabajo. En la mayoría de los casos reales sobre el cuerpo actúan más de una fuerza, por ejemplo, si bajamos un cubo al fondo de un pozo a través de una cuerda que gira en una polea, para coger con él agua, sobre el cubo actúan dos fuerzas, la tensión en la cuerda y la fuerza de la gravedad. Si el descenso del cubo es lento y a velocidad constante es por qué estamos haciendo en la cuerda una fuerza que anula la gravedad, en este caso la fuerza neta es cero y por tanto el trabajo es también cero. No obstante, podemos decir que la cuerda está haciendo trabajo negativo sobre el cubo en la misma magnitud, pero de dirección contraria al que hace la gravedad que es positivo, y, de hecho, el trabajo neto en cualquier punto del recorrido es cero porque sus signos se anulan mutuamente.
Trabajo en sistemas de dos y tres dimensiones.
Ya sabemos que la energía cinética tiene una dependencia cuadrática de la velocidad del cuerpo portador de la energía, y como el cuerpo puede moverse en una sola dirección, la energía cinética tiene una referencia uni-direccional, esto significa que es dependiente solamente de la magnitud de la velocidad, es decir de la rapidez. Ahora trataremos de extender los conceptos de energía cinética, trabajo y el teorema trabajo-energía a dos y tres dimensiones. Continuemos asumiendo que la fuerza neta es constante, pero ahora debe utilizarse su naturaleza plena de vector, al igual que con el desplazamiento, la velocidad y la aceleración (dejaremos de utilizar el sub-índice "net" de la fuerza para reducir la complejidad de la escritura de las expresiones).
La aplicación de la energía y el trabajo en dos y tres dimensiones se simplifica, porque las fuerzas y sus efectos sobre el movimiento se pueden aplicar de forma independiente en las diferentes direcciones cartesianas.
Usemos un sistema bi-direccional por simplicidad. En este caso la ecuación 3, que relaciona el trabajo y la energía se puede descomponer en dos expresiones de acuerdo a la dirección de los ejes cartesianos como:
Fx Δx = ½mvx2 - ½mvx02 (ecuación 8)
Fy Δy = ½mvy2 - ½mvy02 (ecuación 9)
Donde tanto la fuerza, como la velocidad y el desplazamiento han sido separados en sus componentes. Ya sabemos que la energía cinética, depende de la magnitud de la velocidad, es decir de la rapidez, si sumamos los dos componentes cuadráticos x e y de la magnitud de la velocidad de las ecuaciones 8 y 9 llegamos a que la rapidez es:
v2 = vx2 + vy2 (ecuación 10)
La suma ejecutada nos hace llegar a la expresión generalizada del teorema trabajo-energía:
Fx Δx + Fy Δy = ½mv2 - ½mv02 (ecuación 11)
Extendiendo el razonamiento a tres dimensiones llegamos a que para una fuerza F constante:
w = Fx Δx + Fy Δy + Fz Δz (ecuación 12)
Video de Teorema de trabajo y energia cinetica
3. Aplicación de la potencia mecánica en la industria y la tecnología
Definición de potencia
Antes de entrar a establecer el significado del término potencia mecánica, es necesario que acudamos a determinar su origen etimológico:
-Potencia es una palabra que deriva del latín, concretamente de “potentia”, que puede traducirse como “cualidad del que tiene el poder” y que se compone de tres partes diferenciadas: el verbo “posse”, que es equivalente a “poder”; la partícula “-nt”, que se usa para indicar “agente”; y el sufijo “-ia”, que indica “cualidad”.
-Mecánica, por su parte, procede del griego, de “mekhanikos”. Este significa “relativo a la máquina” y se estructura a partir de la suma de los siguientes elementos: el sustantivo “mekhane”, que puede traducirse como “máquina”, y el sufijo “-ico”, que es sinónimo de “relativo a”.
El concepto de potencia puede emplearse para nombrar a la cantidad de trabajo que se desarrolla por una cierta unidad de tiempo. Puede calcularse, en este sentido, dividiendo la energía invertida por el periodo temporal en cuestión. En el lenguaje coloquial, potencia es sinónimo de fuerza o poder
Mecánica, por su parte, es algo que ejerce un mecanismo o aquello que puede provocar diversos efectos físicos, como una erosión o un choque. También se trata de la rama de la física dedicada a estudiar el movimiento y el equilibrio de los cuerpos que se someten a una fuerza.
Con esto en mente, podemos definir qué es la potencia mecánica. Se trata del trabajo desarrollado por una persona o por una maquinaria en un determino espacio temporal. La potencia mecánica, en este sentido, es aquella transmitida mediante la puesta en marcha de un mecanismo o el ejercicio de la fuerza física.
Un ejemplo de potencia mecánica lo encontramos en el accionar de un grúa que debe levantar una carga. Supongamos que se necesita levantar un contenedor para depositarlo adentro de un camión. Debido a que el contenedor es muy pesado, ninguna persona puede moverlo. Se utiliza, por lo tanto, una grúa que está en condiciones de desarrollar una potencia mecánica superior a aquella que puede conseguir cualquier individuo. De este modo, la grúa levanta el contenedor y lo deposita en el camión que se encargará de su transporte.
Además de todo lo expuesto, podemos establecer otros datos importantes acerca de la potencia mecánica:
-Se mide en watts (W). Un watt equivale a un joule (j) de trabajo por segundo (s).
-Gracias a la potencia mecánica podemos calcular la rapidez o lentitud con la que podemos realizar un trabajo en un determinado periodo de tiempo. Un dato interesante a la hora de llevar a cabo, por ejemplo, construcciones de diversa índole.
-Además de los dispositivos ya citados, como las grúas, tenemos que saber que existen otras muchas máquinas en las que poder hacer uso y aplicación del concepto de potencia mecánica. Con eso nos estamos refiriendo a excavadoras, manipuladoras de tipo telescópico e incluso a carretillas elevadoras.
Ver mas sobre potencia ..
Aplicación de la potencia mecanica en las industrias
4. Energía potencial mecánica y energía potencial elástica
¿Qué es la energía Potencial mecánica?
Entendemos por energía mecánica aquella que un cuerpo o un sistema obtienen a raíz de la velocidad de su movimiento o su posición específica, y que es capaz de producir un trabajo mecánico. En líneas generales, la energía mecánica involucra tanto la energía cinética, la energía elástica y la energía potencial de un objeto.
La energía mecánica se conserva en los campos conservativos y en los que forman partículas de acción puramente mecánica, manteniéndose así constante en el tiempo, de acuerdo a la siguiente formulación:
Emec = Ec + Ep + Ee =cte.
En donde Ec es la energía cinética del sistema, Ep su energía potencial gravitatoria y Ee su energía potencial elástica.
Esto no ocurre en sistemas de partículas cargadas de movimiento (pues la energía mecánica se transforma en electromagnética), o en sistemas termodinámicos que atraviesan cambios de estado (la convierten en energía térmica) o en la mecánica de los medios continuos disipativos (en los que la energía se disipa debido a deformaciones y generación de calor).
La energía mecánica es frecuentemente utilizada para realizar trabajos puntuales o convertirla en otras formas de energía, como es el caso de la energía hidráulica, que aprovecha la energía potencial del agua que cae; la energía eólica, que aprovecha la energía cinética del viento, o la energía mareomotriz, que aprovecha la energía cinética de las mareas.
Existen dos tipos de energía mecánica, como se ha visto. Estos son:
Energía cinética. Aquella que se deriva del movimiento de los objetos o sistemas, y que tiene que ver con su velocidad y su desplazamiento. Por ejemplo, una bola en movimiento.
Energía potencial. Aquella que tiene que ver con la posición o la forma de los objetos o sistemas, de los que depende una capacidad de trabajo, y que puede a su vez ser de dos tipos:
- Energía potencial gravitatoria. Aquella que se debe a la acción de la gravedad sobre los cuerpos, como es el caso de un objeto que cae de una altura.
- Energía potencial elástica. Tiene que ver con la constitución y forma del material del objeto, que tiende a recuperar su forma original luego de haber sido sometido a fuerzas que lo deformen, como es el caso de un resorte de metal.
Ejemplos de energía mecánica
Algunos ejemplos posibles de energía mecánica en sus diferentes formas son los siguientes:
Un carrito de montaña rusa. En su punto más alto del ascenso, el carrito habrá acumulado suficiente energía potencial gravitatoria (debido a la altura) para caer libremente un segundo después y convertirla toda en energía cinética (debido al movimiento) y alcanzar velocidades de vértigo.
Un molino de viento. La energía cinética del viento le brinda un empuje que las aspas del molino atrapan y convierten en trabajo mecánico: hacer girar el engranaje que molerá, más abajo, los granos o el trigo del campesino.
Un péndulo. El ejemplo clásico de cómo la energía potencial gravitatoria del peso se convierte en energía cinética para hacerlo mover en su recorrido, conservando la energía mecánica total.
Como se ha dicho ya, la energía mecánica puede dividirse en dos formas: la cinética (movimiento) y la potencial (forma o posición).
La primera es calculable mediante la fórmula simple de Ec = ½ m . v2 y su unidad de medición en el Sistema Internacional serán los Joules (J).
En cambio, la energía potencial se trata de la cantidad de energía almacenada en el sistema, debido a su configuración particular o a su posicionamiento respecto a un campo gravitacional o electromagnético, según sea el caso. Esta energía es susceptible de convertirse en otras formas de energía, como la cinética misma.
5. Aplicación de la Ley de Conservación de la Energía en las energías alternativa
Ley de la conservación de la energía. Constituye el primer principio de la termodinámica y afirma que la cantidad total de energía en cualquier sistema aislado (sin interacción con ningún otro sistema) permanece invariable con el tiempo, aunque dicha energía puede transformarse en otra forma de energía.
Es una de las leyes fundamentales de la física y su teoría se trata de que la energía no se crea ni se destruye, únicamente se transforma; ello implica que la masa en ciertas condiciones se puede considerar como una forma de energía.
La ley de la conservación de la energía es considerada una de una de las leyes fundamentales de la física y constituye el primer principio de la termodinámica. Plantea que la energía total de un sistema aislado permanece constante o que la energía no se crea ni se destruye, únicamente se transforma lo que implica que en ciertas condiciones la masa se puede considerar como una forma de energía.
La ley de conservación de la energía afirma que no existe ni puede existir nada capaz de generar energía, no existe ni puede existir nada capaz de hacer desaparecer la energía y por último si se observa que la cantidad de energía varía, siempre será posible atribuir dicha variación a un intercambio de energía con algún otro cuerpo o con el medio circundante.
La energía es la capacidad de los cuerpos o sistemas de cuerpos para efectuar un trabajo. Todo sistema que pasa de un estado a otro produce fenómenos físicos o químicos que no son más que manifestaciones de alguna transformación de la energía, pues esta puede presentarse en diferentes formas: cinética, potencial, eléctrica, mecánica, química. Siempre que se produzca una cantidad de una clase de energía se deberá consumir una cantidad exactamente equivalente de otra clase o clases.
Cuando un sistema se encuentra en un estado particular se caracteriza por un valor de su energía interna que es la sumatoria de la energía cinética y potencial de todas las partículas que componen el sistema. Al tomar la energía interna como un todo, no es necesario especificar los diferentes tipos de energía intrínsecos de las partículas componentes. Esto significa que cualesquiera que sean las interacciones del sistema con los alrededores, la energía que este cede o recibe de ellos se traduce exclusivamente en un aumento o disminución de su energía interna (U) lo cual simplifica extraordinariamente el estudio del sistema y sus interacciones. La energía interna (U) se mide en Joule (J).
Dentro de los sistemas termodinámicos, una consecuencia de la ley de conservación de la energía es la llamada primera ley de la termodinámica, la cual establece que, al suministrar una determinada cantidad de calor (Q) a un sistema, esta cantidad de energía será igual a la diferencia del incremento de la energía interna del sistema (ΔU) más el trabajo (W) efectuado por el sistema sobre sus alrededores.
Más información sobre la ley de la conservación de la energía