Dibujo Técnico Aplicado a los Diseños y Proyectos Productivos
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 5° - Artes Plásticas y Visuales |
| Libro: | Dibujo Técnico Aplicado a los Diseños y Proyectos Productivos |
| Impreso por: | Invitado |
| Fecha: | sábado, 5 de abril de 2025, 18:39 |
1. Perspectiva de: uno, dos y tres puntos: aplicaciones
El dibujo en perspectiva es una técnica de dibujo que se emplea para representar la profundidad espacial, a la que llamamos perspectiva. Dicho de otro modo, sirve para representar correctamente un objeto tridimensional en un plano bidimensional.
Tradicionalmente se conocen tres tipos de dibujo de perspectiva: de un punto de fuga (paralela), de dos (oblicua) o de tres (aérea).
Perspectiva de un punto de fuga (perspectiva paralela):

La perspectiva de un punto de fuga o paralela se suele usar para composiciones en las que los objetos se observan de frente.
Las líneas que se extienden desde la parte frontal hasta el fondo, se encuentran o convergen en un punto. El punto donde convergen se llama "punto de fuga".
El punto de fuga siempre descansa en una línea horizontal a la altura de los ojos, a la que llamamos "línea de horizonte", y representa la altura a la que se encuentran los ojos de la cámara o del observador.
Perspectiva de dos puntos de fuga (perspectiva oblicua):
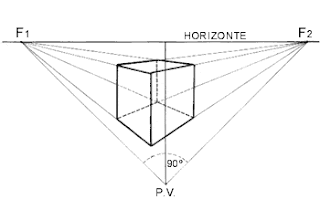
La perspectiva de dos puntos de fuga u oblicua se suele usar para composiciones en las que los objetos se observan desde un ángulo. Es la que más se parece a la que tiene el ojo humano, así que es la que más se usa a la hora de dibujar ilustraciones o los fondos de un cómic.
En la perspectiva de un punto las líneas convergen en un punto que se extiende desde el fondo hasta el primer plano. En la perspectiva de dos puntos de fuga, además de la profundidad, tenemos líneas convergentes que representan también la anchura.
Perspectiva de tres puntos de fuga (perspectiva aérea):
La perspectiva de tres puntos de fuga o aérea es la que se usa para composiciones en las que se observa un objeto desde abajo o desde arriba.
En la perspectiva de dos puntos las líneas que representan la profundidad y la anchura convergen en dos puntos de fuga diferentes.
En la perspectiva de tres puntos, las líneas que representan la altura se extienden hasta un tercer punto de fuga.
Para composiciones en las que se mira un objeto desde abajo, el punto de fuga de la altura está por encima del objeto.
2. Perspectiva cónica: frontal y oblicua
Perspectiva Cónica Frontal
Esta es una obra de Antonio Rojas, llamada ‘Light After Light’, donde el pintor pone a prueba el espacio pictórico para desarrollar sus imágenes mentales. Nos encontramos atrapados en un espacio al que buscamos sus límites. La percepción que este autor tiene de la realidad se perece muy poco a lo que se entiende como normal. Definitivamente la naturaleza de estas imágenes no es realista.

Podemos ver cómo las líneas horizontales y verticales no se desvían y siguen manteniéndose paralelas entre sí y perpendiculares con las otras. Pero si nos fijamos en las líneas de profundidad (en negro) podemos apreciar como líneas que son paralelas, en la realidad se van acercando hasta que convergen en un único punto, que en este caso se trata aproximadamente del centro de la obra.

Esta obra pertenece a Leonardo Da Vinci, y se llama ‘La Última Cena’. Leonardo utiliza en la obra tres formas de conseguir un espacio tridimensional. Por una parte las paredes y el techo crean líneas de fuga a través de los tapices y casetones que nos conducen hacia la pared del fondo.

Perspectiva Cónica Oblicua
Esta obra titulada ‘La Anunciación’ pertenece a Fra Angelico, y se muestra en los edificios justamente detrás de estas personas, los puntos en donde se conectan las líneas de fuga. En este caso aparecen varios puntos de fuga.

Este caso es especial. Esta obra se titula ‘La iglesia de Auvers-sur-Oise’,
de Van Gogh, aparece como ejemplo de perspectiva cónica oblicua en pintura en
varios manuales, pero dado el carácter expresivo del autor y el resultado final
del cuadro, no consideramos que su preocupación fuera la exactitud minuciosa de
la perspectiva.

3. Perspectiva axonómetrica: Isométrica, dimétrica y trimétrica
Perspectiva axonométrica
La proyección axonométrica es una proyección sobre un plano (Axonométrico) que tiene una posición arbitraria en el espacio. Si los rayos son perpendiculares al plano axonométrico, se trata de una proyección axonométrica ortogonal. Este sistema de proyección es muy similar a la manera de observar los objetos en el espacio, conservándose, sin embargo, todas las propiedades de la proyección cilíndrica (paralelismo, perpendicularidad).
Las proyecciones del plano axonométrico en el plano horizontal XY determina la recta XY cuya proyección es perpendicular al eje Z. En efecto: Ambas rectas (eje Z y XY) son ortogonales, la recta XY está contenida en el plano axonométrico y la proyección axonométrica es una proyección ortogonal.

Elementos del Sistema de Proyección:
Los elementos de un sistema de proyección son:
· Tres planos perpendiculares (denominado triedro trirrectangular).
· Las rectas donde se cortan los tres planos coordenados (denominados ejes).
· Corte de los tres ejes (denominado vértice).
Coordenadas y escalas
Se pueden medir las coordenadas de los puntos sobre los ejes, tomando en cuenta la deformación correspondiente de estos. (De allí se deriva el nombre axonométrica que en griego significa medida sobre los ejes).
Cada eje tiene su escala predeterminada de acuerdo con el plano axonométrico y su respectiva dirección de los rayos de proyección. Todas las líneas paralelas al plano axonométrico se conservan en esta proyección en verdadero tamaño. Para determinar las escalas sobre los ejes, rebatimos estos sobre el plano axonométrico donde se deben proyectar en verdadero tamaño. Para definir la proyección axonométrica basta fijar los ángulos bajo los ejes X, Y, Z, cuya suma debe ser 360º y ninguno puede ser 90º. También se puede definir mediante el triángulo axonométrico.
Trimetría: los tres ángulos son distintos, las tres escalas son distintas.
Bimetría: dos ángulos son iguales y dos escalas también son iguales (la escala distinta esta sobre el eje opuesto al ángulo distinto).
Isometría (Monometría): los tres ángulos son iguales a 120º, las tres escalas son también iguales.
Características de la proyección axonométrica
La proyección axonométrica es una proyección cilíndrica, ortogonal donde se conserva: Propiedades:
a) El paralelismo y la proporcionalidad, así como los diámetros conjugados de una cónica.
b) El plano axonométrico se proyecta en su verdadero tamaño.
c) La recta perpendicular a una recta paralela al plano axonométrico se proyecta bajo un ángulo recto en ella.
d) Una esfera se proyecta como una circunferencia.
Uso: La proyección axonométrica se usa ventajosamente para representar esquemas de instalaciones, piezas mecánicas, edificios, etc. Da una ilusión más parecida al objeto que la proyección oblicua ya que se acerca más a la manera de mirar (pero a veces es más laborioso efectuarla.
Representación y visibilidad: Se acostumbra repasar únicamente la proyección (perspectiva) aunque la proyección horizontal es igualmente indispensable.
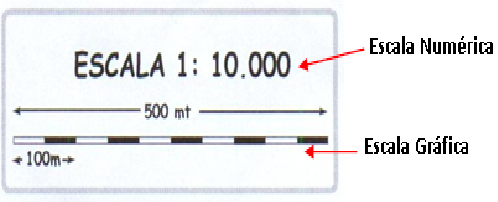
4. Escala numérica y gráfica
Escala numéricaLa escala numérica se expresa normalmente mediante una fracción cuyo numerador (la unidad) es la medida en el mapa y el denominador la medida correspondiente en el terreno. La escala numérica que aparece en la leyenda de los mapas y su uso en el cálculo de las distancias o áreas es de precisión.
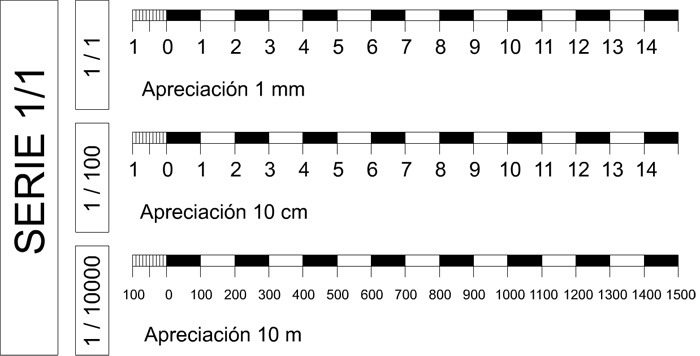
Escala gráfica
Es una línea graduada por medio de la cual las distancias en la carta o mapa se pueden medir directamente en términos de distancias en el terreno. Es la que aparece en la leyenda de los documentos cartográficos en forma de barras mediante líneas paralelas graduadas y numeradas en kilómetros. La escala de barras es la que señala en forma gráfica las distancias reales en el mapa.