MOVIMIENTO CIRCULAR EN EL UNIVERSO Y EN EL ÁTOMO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Ciencias Naturales: Física |
| Libro: | MOVIMIENTO CIRCULAR EN EL UNIVERSO Y EN EL ÁTOMO |
| Impreso por: | Invitado |
| Fecha: | viernes, 22 de noviembre de 2024, 11:19 |
1. Relación angular y lineal
Relación entre las magnitudes angulares y lineales
Magnitudes lineales y angulares
De la definición de radián (unidad natural de medida de ángulos) obtenemos la relación entre el arco y el radio. Como vemos en la figura, el ángulo se obtiene dividiendo la longitud del arco entre su radio
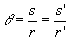
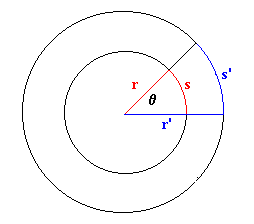
Derivando s=rq respecto del tiempo obtenemos la relación entre la velocidad lineal y la velocidad angular
La dirección de la velocidad es tangente a la trayectoria circular, es decir, perpendicular a la dirección radial
Derivando esta última relación con respecto del tiempo obtenemos la relación entre la aceleración tangencial at y la aceleración angular.
Existe aceleración tangencial, siempre que el módulo de la velocidad cambie con el tiempo, es decir, en un movimiento circular no uniforme.
El cálculo de la componente normal de la aceleración es algo más complicado. La aceleración normal está relacionada con el cambio de la dirección de la velocidad con el tiempo. En un movimiento circular uniforme no existe aceleración tangencial ya que le módulo de la velocidad no cambia con el tiempo, solamente cambia su dirección y por tanto, solamente existe aceleración normal.
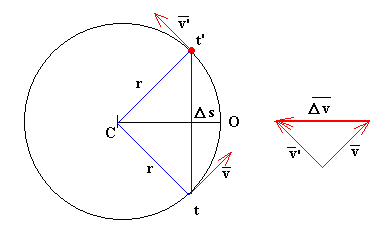
Supongamos
un móvil que describe un movimiento circular uniforme. Calculemos el cambio de
velocidad
que
experimenta el móvil entre los instantes t y t', tal como se ve
en la figura. El vector
tiene dirección radial y sentido hacia el centro
de la circunferencia. Los triángulos de color rojo y de color azul de la figura son
isósceles semejantes por lo que podemos establecer la siguiente relación
Dividiendo ambos miembros entre el intervalo de tiempo Dt=t'-t
Cuando el intervalo de tiempo Dt tiende a cero, la cuerda Ds se aproxima al arco, y el cociente ds/dt nos da la velocidad v del móvil
La aceleración normal an tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil y su módulo viene dado por una u otra de las expresiones siguientes:
La velocidad de un móvil en movimiento circular tiene la dirección tangente a la circunferencia.
Existe aceleración tangencial at siempre que cambie el módulo de la velocidad con el tiempo. El sentido de la aceleración tangencial es el mismo que el de la velocidad si el móvil acelera, y es de sentido contrario si se frena. En un movimiento circular uniforme no hay aceleración tangencial.
En un movimiento circular siempre existe aceleración normal, an ya que cambia la dirección de la velocidad con el tiempo. La aceleración normal tiene dirección radial y sentido hacia el centro de la circunferencia que describe el móvil.
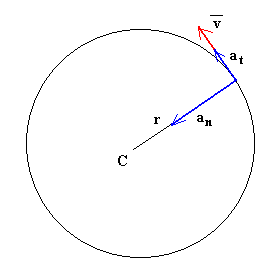
La aceleración total del móvil se obtiene sumando vectorialmente ambas componentes de la aceleración
Ver más en el video
2. Aceleración y fuerza centrípeta
Aceleración centrípeta
En un movimiento circular cualquiera, la aceleración puede tener una componente en dirección tangencial a la circunferencia y otra componente en dirección radial y dirigida hacia el centro de la trayectoria. A la primera se le llama aceleración tangencial y a la segunda, aceleración centrípeta.
La aceleración tangencial se manifiesta como un cambio en el módulo de la velocidad tangencial, mientras que la aceleración centrípeta aparece como un cambio en la dirección y sentido de la velocidad.
En un movimiento circular uniforme, debido a que el módulo de la velocidad tangencial es constante, solo existe una aceleración que cambia la dirección y el sentido de la velocidad, es decir, la aceleración centrípeta.
El cambio del vector velocidad tangencial apunta hacia el
centro de curvatura, al igual que la aceleración centrípeta ac.
Si se considera el cambio de velocidad, ∆v = v f − vi , que experimenta un móvil en un pequeño intervalo de tiempo ∆t , se ve que ∆v es radial y está dirigido hacia el centro curvatura. La aceleración, por lo tanto, también tiene esa dirección y sentido, y por eso se denomina aceleración centrípeta.
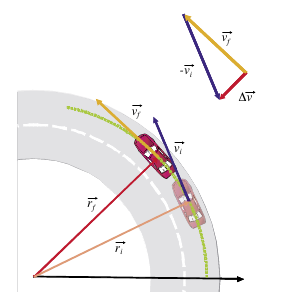
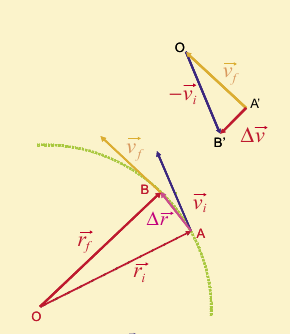
Si consideramos un intervalo de tiempo muy pequeñísimo y considerando las relaciones geométricas de la figura anterior tenemos:
Como hemos aprendido, la aceleración es una consecuencia de la aplicación de una fuerza neta sobre el cuerpo, por lo que la aceleración centrípeta tendrá la misma dirección y sentido que la fuerza centrípeta, bastará sólo con multiplicar la masa del cuerpo en cuestión por la aceleración.
Ejercicios sobre aceleración centripeta
Fuerza centrípeta La fuerza centrífuga la encontramos todos los días y en cada
momento de nuestra vida cotidiana. Lo experimentamos cuando doblamos en una
esquina en un automóvil o cuando un avión se inclina hacia un giro son típicos
ejemplos de ella. Algunas personas pueden confundir la fuerza centrípeta
con su contraparte, la fuerza centrífuga, porque están tan estrechamente
relacionadas. Sin embargo, son diferentes, la fuerza centrípeta se define como,
el componente de fuerza que actúa sobre un cuerpo en movimiento curvilíneo que
se dirige hacia el centro de curvatura o eje de rotación. ¿Qué es la fuerza centrípeta? Es cuando algún objeto que describe una trayectoria de forma
circular, por situaciones de la fuerza que es ejercida por quien hace la
acción, tiene la sensación de ser llevado al interior del centro de la circunferencia
que se describe. En qué consiste la fuerza centrípeta La fuerza centrípeta es un sistema que funciona cuando un
determinado objeto se mueve en dirección curvilínea. Este tipo de fuerza
actuará de forma perpendicular con respecto a la dirección, en este caso, la gravedad
operará como un agente contrario, puesto que, si la velocidad cambia, sobre el
objeto se aplicará un cambiante de centrifuga que ayudará a mantener el trayecto
sencillamente uniforme. La etimología de la palabra nos dice que la palabra proviene
del término “Centrípeta” la cual proviene de la combinación de “centrum”
palabra que hace referencia al centro del vórtice y “petere” que quiere decir “dirigirse
hacia”, es decir, dirigirse hacia el centro. Cómo se calcula Para poder calcular la fuerza centrípeta se utiliza una
fórmula F = – (m·v2/r) ur = – m·w2·r = m·a a = – w2·r Donde: F: fuerza centrípeta. El newton (N) es la unidad de
medida en el Sistema Internacional (S.I.). m: Masa del cuerpo. El kilogramo (kg) es la unidad de
medida en el Sistema Internacional. v: módulo de la velocidad. Se mide en metros por segundo
(m/s). Ur: vector unitario radial r: radio de la trayectoria circular w: velocidad angular medida en rad/s a: aceleración centrípeta medida en m/s² Aplicaciones de la fuerza centrípeta La fuerza centrípeta es generalmente utilizada en las centrífugas
de laboratorio. Aquí, las partículas que se encuentran suspendidas en un
líquido se separan del líquido acelerando los tubos orientados de modo que las
partículas más pesadas se dirijan hacia el fondo de los tubos. Mientras que las centrifugadoras suelen separar sólidos de
líquidos, también pueden fraccionar líquidos, como por ejemplo en muestras de
sangre o componentes separados de gases. Las centrífugas de gas se utilizan
para separar el isótopo más pesado uranio-238 del isótopo más ligero
uranio-235. El isótopo más pesado es atraído hacia el exterior de un cilindro
giratorio. La fracción pesada se gira y se envía a otra centrífuga. Se puede hacer un telescopio reflector líquido girando un
metal líquido reflectante, como el mercurio. Importancia La fuerza centrípeta es de suma importancia ya que ponen y
ayudan a que los objetos o cuerpos a los cuales se les está aplicando las fuerzas
logren mantenerse en equilibrio y al mismo tiempo ayuda a resolver diferentes
problemas con ecuaciones. Diferencia entre fuerza centrípeta y fuerza centrífuga La fuerza centrífuga es la tendencia que tiene un objeto a
seguir un camino curvo que se aleja del centro de la misma curva. Básicamente
ésta no es realmente una fuerza, sino más bien es un resultado de la inercia,
que es la tendencia de un objeto a resistirse al cambio ya sea que esté en
movimiento o no. La fuerza centrípeta, es una fuerza real que tiene la
capacidad de contrarrestar la fuerza centrífuga y evitar que el cuerpo en
cuestión “salga volando”, ya que lo mantiene en movimiento a una velocidad
constante y con una trayectoria circular. Ejercicios de fuerza centrípeta
3. Aceleración angular
Aceleración angular
Definimos aceleración angular como los cambios que experimenta la velocidad en las unidades de tiempo. Hacemos referencia a ella con la letra griega alfa α. Igual que la velocidad angular, la aceleración es de una corriente vectorial.
Se define aceleración angular como el canje que sufre la velocidad en las unidades de tiempo. Se la denomina como alfa α. Así como la velocidad angular, la aceleración angular presenta carácter vectorial.
La expresamos en s-2 que representa los radianes por segundo al cuadrado y esto es porque el radián es adimensional. Por ende la aceleración angular mantiene el eje de rotación que se mantiene en una dirección constante en el espacio.
Definimos como vector de aceleración angular en su ecuación como:
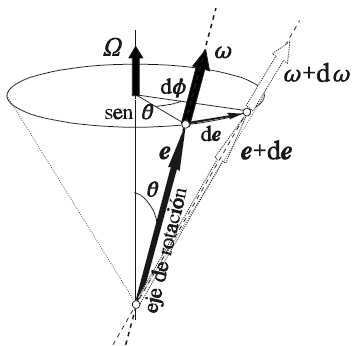
El vector de velocidad angular de un cuerpo contorno del eje de rotación lo denominamos e y al versor asociado de dicho eje se denomina w, del modo que tenemos w = we.
En el caso individual en que este eje de rotación mantiene su orientación fija, el espacio entonces será de/dt = 0 y su vector asociado en este caso alfa, se localiza referente el eje de rotación. Implementándose de la siguiente manera:
De esta forma el módulo de la aceleración angular |α| = α, como la derivada de la aceleración angular respecto al modo angular del tiempo, su dirección es aquella que corresponde al eje de rotación. Por otro lado el sentido es la w cuando la aceleración angular se incrementa con el tiempo, pero a su vez el sentido opuesto comienza a disminuir.
Cuando el eje de rotación no conserva la dirección precisa en el espacio será
,sin embargo
,
Porque el versor de este eje cambia de dirección por el transcurso en el que el movimiento de e es un versor, la derivada se presentará como un vector perpendicular a e, todo ello respecto al eje instantáneo de rotación.
En ese caso lo más general de aceleración angular de alfa que se expresa de la siguiente manera
Siendo gama la velocidad angular referida a la rotación o precesión de este eje de rotación. En la fórmula debemos observar que el vector aceleración tiene dos componentes básicos. Los dos componentes longitudinales cuyo módulo es
Los componentes transversales, perpendiculares al eje rotación cuyo módulo gama x W son la segunda característica de este tipo de cálculos.
El vector de expresión anterior que observamos denominado alfa no presentará similar dirección y aceleración que el vector W.
El vector de aceleración angular alfa no tendrá por ende una dirección en su eje de rotación.
En los movimientos planos de un sólido rígido la aceleración angular al igual que la velocidad, tienen una dirección de eje de rotación y es dado por:
Esperamos que mediante el uso de este artículo te hayan quedado claro que las funciones planteadas para ser utilizadas deben ser implementadas en el sentido de que no hay una muy buena relación entre los teoremas y los axiomas por lo que recomendamos basarse en las situaciones en que lo elementos pre indicados puedan ser llevados al cociente de la moción.
Ver más sobre velocidad angular
4. Velocidad angular media
Velocidad angular media
La velocidad angular media de rotación se define como el ángulo girado por unidad de tiempo del vector posición de un punto que describe movimiento circular. Las aspas de un ventilador de techo (como el mostrado en la figura 1), siguen movimiento circular y su velocidad angular media de giro se calcula tomando el cociente entre el ángulo girado y el tiempo en que se recorrió ese ángulo.
Las reglas que sigue el movimiento de rotación son de cierta manera semejantes a las ya familiares del movimiento traslacional. Las distancias recorridas pueden medirse en metros también, sin embargo las magnitudes angulares cobran especial relevancia porque facilitan en gran medida la descripción del movimiento.
Por lo general se utilizan letras griegas para las magnitudes angulares y letras latinas para las correspondientes magnitudes lineales.
Definición y fórmulas
En la figura 2 se representa el movimiento de un punto sobre una trayectoria circular c. La posición P del punto corresponde al instante t y la posición angular correspondiente a ese instante es ϕ.
A partir del instante t transcurre un lapso de tiempo Δt. En ese lapso la nueva posición del punto es P’ y la posición angular se ha incrementando un ángulo Δϕ.
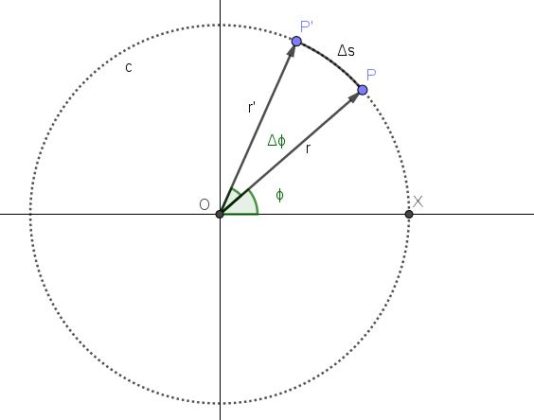
Figura 2. Movimiento circular de un punto. Fuente: elaboración propia
Ejercicio
Las puntas de las aspas del ventilador de techo mostrado en la figura 1 se mueven con una rapidez de 5 m/s y las aspas tienen 40 cm de radio.
Con estos datos calcule: i) la velocidad angular media de la rueda, ii) el número de vueltas que da la rueda en un segundo, iii) el periodo en segundos.
Solución
i) La rapidez lineal es v=5 m/s.
El radio es r= 0,40 m.
De la relación entre rapidez lineal y rapidez angular despejamos esta última:
v = r・ω => ω = v/r = (5 m/s)/(0,40 m) = 12,57 rad/s
ii) ω = 2π・f => f = ω / 2π = (12,57 rad/s) / ( 2π rad) = 2 vuelta/s
iii) T= 1 / f = 1 / (2 vuelta/s) = 0,5 s por cada vuelta.
Más sobre velocidad angular media