EL MOVIMIENTO ACELERADO EN EL DESARROLLO TECNOLÓGICO
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Ciencias Naturales: Física |
| Libro: | EL MOVIMIENTO ACELERADO EN EL DESARROLLO TECNOLÓGICO |
| Impreso por: | Invitado |
| Fecha: | sábado, 23 de noviembre de 2024, 15:30 |
1. Aceleración promedio e instantánea en movimiento unidimensional.
Aceleración media e instantánea
La velocidad y la aceleración tienen una mutua relación, sin embargo suele confundirse, se puede decir que la velocidad es el espacio recorrido en un lapso de tiempo determinado y la aceleración seria si la velocidad de una partícula cambia con el tiempo entonces decimos que la partícula tiene una aceleración, es decir la aceleración describe la razón de cambio de la velocidad con el tiempo, la aceleración se describe como una cantidad vectorial.
La diferencia es que, la aceleración describe cómo cambia la velocidad con el tiempo y la velocidad describe el cambio de la posición de una partícula con el tiempo.
Aceleración media
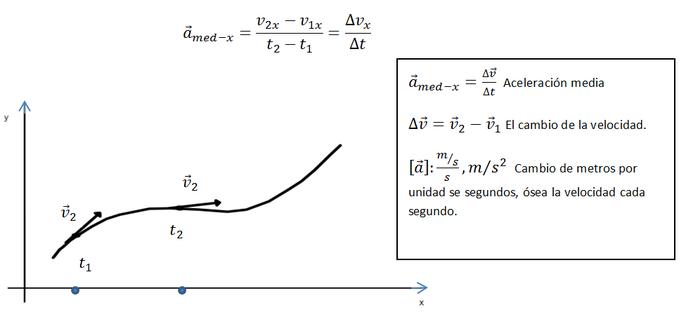

La velocidad y la aceleración tienen una mutua relación, sin embargo suele confundirse, se puede decir que la velocidad es el espacio recorrido en un Ejemplo
Un automóvil parte de una posición 0 m, con 0 velocidad inicial, en 6 segundo se encuentra a 10 m, del punto de partida con una velocidad de 3m/s, a este llamaremos punto A, y 14 segundos después de haber salido del punto de partida se encuentra a 46 m del punto de partida con una velocidad de 7m/s, a este llamaremos punto B.
a) Determine la velocidad media del punto A al punto B.
b) Determinar la aceleración media del punto A al punto B.
En el siguiente problema necesitamos al menos dos expresiones que nos permitan encontrar los valores que necesitamos es decir velocidad media y aceleración media tenernos la información que necesitamos y a partir de ello vamos a operar.
Plantear
Es necesario seguir un orden en los procedimientos operacionales por la coherencia de los mismos, en este casos encontraremos primero la velocidad media posterior mente la aceleración media entre los dos puntos A y B.
Ejecutar
a) Para encontrar la velocidad media necesitamos realizar la siguiente operación

b) La aceleración media la podemos calcular mediante la siguiente expresión

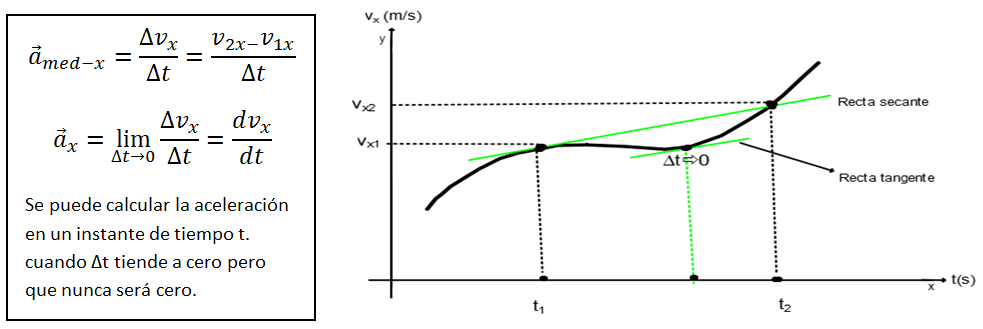
El movimiento unidimensional es aquel en el que el móvil está obligado a desplazarse siguiendo una línea determinada. Se distinguen dos tipos de movimientos, a saber:
1. Movimiento Horizontal: Es aquel en el que el móvil se desplaza en línea recta en sentido horizontal, a lo largo del eje x. Ejemplos de este movimiento pueden ser:
Vehículos desplándose a velocidad constante.
Carros, trenes, etc. acelerado.
Carros, trenes, etc. frenado.
2. Movimiento Vertical: Es aquel en el que el móvil se desplaza en línea recta en sentido vertical, a lo largo del eje y. Ejemplos de este movimiento pueden ser:
Globo Aerostático.
Paracaídas.
Lanzamientos verticalmente ascendentes y descendentes.
En función de la variación de la velocidad, el movimiento puede ser rectilíneo uniforme (M.R.U.) y rectilíneo uniformemente variado
Movimiento unidimensional asombró al hombre por siglos. De hecho no fue hasta el trabajo de Gali-leo (Galileo Galilei, italiano, 1564-1642) que el hombre empezó a describir adecuadamente el movimiento de los cuerpos. Para ilustrar el estado de las cosas en los tiempos remotos, basta recordar la célebre paradoja de Cenote Aquiles y la tortuga. De acuerdo a Seno, Aquiles nunca podría alcanzar una tortuga porque para hacerlo primero tendría que alcanzar el punto de donde la tortuga partió. Sin embargo al alcanzarlo, la tortuga se habría movido alguna cantidad, estando de nuevo las cosas igual que al empezar. Este proceso debería ser entonces repetido un número infinito de veces de modo que Aquiles nunca alcanzaría la tortuga .Para la descripción del movimiento, Galileo debió asignar números para medir los conceptos de posición y tiempo, cuestión no fácil aquellos tiempos, por la ausencia de instrumentos adecuados para ello.
Movimiento unidimensional.
Para el movimiento de un cuerpo en una línea recta, la posición del cuerpo puede ser indicada por una variable numérica x llamada suposición respecto algún origen en esa recta. Esa variable indica la distancia del cuerpo al origen expresada en alguna unidad de medida, hoy en día esa unidad es el metro. Se dice que el cuerpo se mueve si dicha variable, denominada coordenada de posición, varía con el transcurso de tiempo. Considere por ejemplo que un cuerpo se mueve de modo que su coordenada de posición x varía con el tiempo de acuerdo al grafico siguiente .La curva de forma parabólica nos indica donde está el cuerpo sobre el eje X en cada tiempo, en particular nos dice que el cuerpo estuvo en el origen.
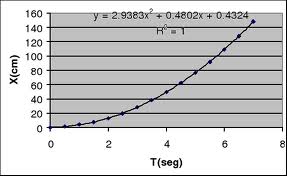
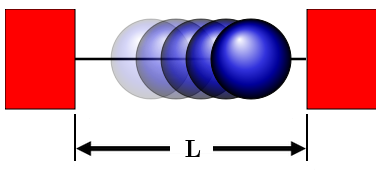
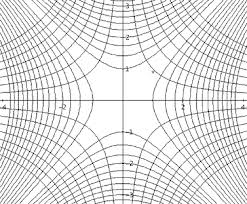
2. Movimiento con aceleración constante de los medios de transporte y cuerpos puntuales en la naturaleza.
Movimiento con aceleración constante.
Como ya hemos visto la aceleración al igual que la velocidad tiene una manera similar de operar la diferencia son los datos, se t1=0 y t2 cualquier instante posterior, podemos encontrar la aceleración media a partir de la siguiente expresión.

Para determinar la posición partiendo de ecuaciones de velocidad y aceleración constante podemos determinarla con una expresión así.
![]()
ambién podemos utilizar una expresión para encontrar el tiempo, realizando los procedimientos obtendremos una expresión así.
![]()
EJEMPLO
Un
automóvil pasa por un poste que sostiene una lámpara, acelera apenas pasa justo
al lado del poste, su aceleración constante es de 3.0m/s^2 , en t=0, está a 4.0m
al este del poste, moviéndose en dirección este a 9m/s.
a) Calcular su
posición en t=3s.
b) calcular su
velocidad en t=5.0s.
c) ¿Dónde está el automóvil
cuando su velocidad es de 40m/s?
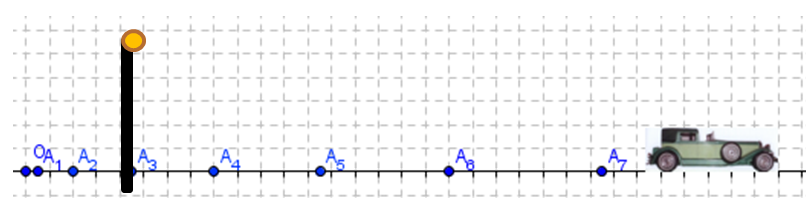
Identificar
Tenemos los datos necesarios para encontrar la posición y la velocidad en un determinado instante, necesitamos al menos 3 expresiones que nos permitan encontrar los datos que necesitamos.
Plantear
Necesitamos una expresión que nos permita operar posición como función del tiempo, dado los datos que se conocen, también necesitamos una expresión que nos permita operar velocidad como función del tiempo y por ultimo una expresión que nos permita operar velocidad como función de la posición.
Ejecutar
a). Para determinar la posición partiendo de los datos que tenemos la siguiente operación nos permitirá operar y encontrar el valor.
![]()
La posición en la que se encontrara el automóvil en 3 segundos será a 44.5m.
b). Para calcular la velocidad en un determinado tiempo conociendo la velocidad como función del tiempo será, donde los sub índices significan final y inicial per que comúnmente solo se coloca una 0 por la i, dejando por entendido que el otro valor es el final, esto dependerá del libro de texto que utilices, pero que no afecta la operación siempre y cuando realizas bien las operaciones.
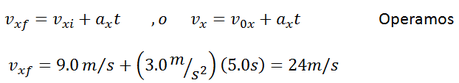
c). Necesitamos calcular partiendo de la velocidad como función de la posición, para determinar donde estará el automóvil cuando su velocidad sea de 40 m/s.

Ver más información en el video
Cuerpos puntuales
Un cuerpo puntual o particula es un objeto considerado sin tamaño,que puede tener movimiento,pero que no existe en la naturaleza.
Un cuerpo no necesita ser pequeño para ser considerado puntual.
Un ejemplo es la helice de un helicoptero gira sobre su eje a medida que avanza.

3. Saberes y conocimientos culturales en movimientos telúricos, sismos y otros.
Información sobre sismo y movimientos teluricos