LOGARITMOS Y EXPONENTES EN LA REALIDAD COTIDIANA
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 4° - Matemáticas |
| Libro: | LOGARITMOS Y EXPONENTES EN LA REALIDAD COTIDIANA |
| Impreso por: | Invitado |
| Fecha: | viernes, 4 de abril de 2025, 14:45 |
1. Definición y cálculo de un logaritmo
Definición de Logaritmo
A instancias de las matemáticas, un logaritmo es el exponente al cual es necesario elevar a una determinada cantidad positiva para que resulte un número determinado. También se lo conoce como la función inversa a la función exponencial.
En tanto, se denomina logaritmación a la operación
matemática a través de la cual, dando un número resultante y una base de
potenciación se tendrá que hallar el exponente al cual habrá que elevar la base
para así conseguir el mencionado resultado.
Tal como sucede con la suma y la multiplicación que tienen sus operaciones opuestas, la
división y la resta, la logaritmación tiene a la exponenciación como su
función inversa.
Ejemplo: 10(2) = 100, el logaritmo de 100 en base 10 será el 2 y se lo
escribirá de la siguiente forma: log10 100 = 2.
Este método
de cálculo
a través de los denominados logaritmos fue impulsado por John Napier a
comienzos del siglo XVII.
El método logarítmico no solamente contribuyó en cuanto al avance de la ciencia
sino que además se convirtió en una herramienta
fundamental en el ámbito de la Astronomía
haciendo más simples cálculos realmente muy complejos.
A los logaritmos se los usó muchísimo en la geodesia, en algunas ramas de la matemática aplicada y en la navegación marítima cuando las calculadoras y las computadoras todavía no eran el hecho concreto que son hoy en día.
Logaritmo concéptos básicos
1.1. Propiedades logarítmicas
Logaritmos y sus propiedades
1- Definición de Logaritmo
Se define logaritmo como el exponente de una potencia con cierta base, es decir, el número al cual se debe elevar una base dada para obtener un resultado determinado.
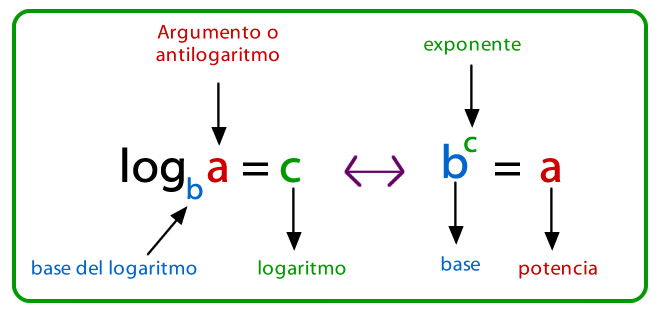
Por ejemplo:
5 0 = 1
51 = 5
52 = 25
53 = 125, etc.
Luego, siendo la base 5, el logaritmo de 1 (que se escribe log5 1) es 0, por que 0 es el exponente al que hay que elevar la base 5 para que dé 1; el log5 5 es 1; el log5 25 es 2, el log5 125 es 3, etc.
- No existe el logaritmo de los números negativos.
El argumento y la base de un logaritmo son números reales positivos. Además, la base no puede ser 1. Es decir, en la expresión logb a, siempre, por definición, a ∈ R+ y b ∈ R+ – {1}.
- El argumento y la base de un logaritmo son números reales positivos. Además, la base no puede ser 1. Es decir, en la expresión logb a, siempre, por definición, a ∈ R+ y b ∈ R+ – {1}.
- Calcula el valor de log0,7 0,343
2- Propiedades
2.1- Logaritmo de la unidad
El logaritmo de 1 en cualquier base es igual a 0.
logb (1) = 0 ; con b ≠ 1.
Ej: log5 (1) = 0 porque 50 =1
log7 (1) = 0 porque 70 = 1
log20 1 = 0 ⇔ 200 = 1
2.2- Logaritmos de la base
El logaritmo de la base es igual a 1.
logb (b) = 1 ; con b ≠ 1.
Ej:
log5 (5) = 1 ⇔ 51 = 5
log6 (6) = 1 ⇔ 61 = 6
log12 (12) = 1 ⇔ 121 = 12
2.3- Logaritmo de una potencia con igual base:
El logaritmo de una potencia de un número es igual al producto entre el exponente de la potencia y el logaritmo del número.
logb bn = n, con b ≠ 1
Ej:
log6 6 3 = 3
2.4- Logaritmo de un producto
El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
logb (a • c) = logb a + logb c
Ej:
logb (5 • 2) = logb 5 + logb 2
2.5- Logaritmos de un cociente
El logaritmo de un cociente es igual al logaritmo del dividendo, menos el logaritmo del divisor.
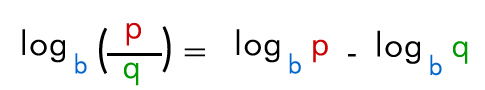
Ej:
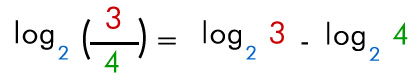
2.6- Logaritmo de una potencia
El logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base.
loga cn = n loga c
Ej:
log3 10 2 = 2 log3 10
2.7- Logaritmo de una raíz
El logaritmo de una raíz es igual al logaritmo de la cantidad subradical dividido entre el índice de la raíz.
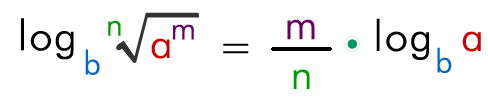
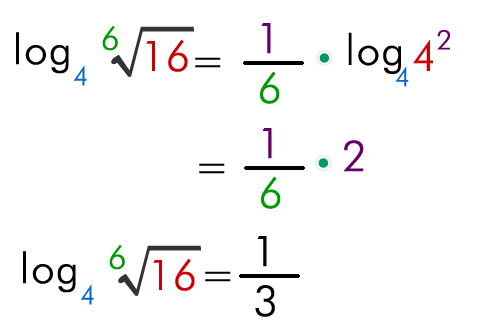
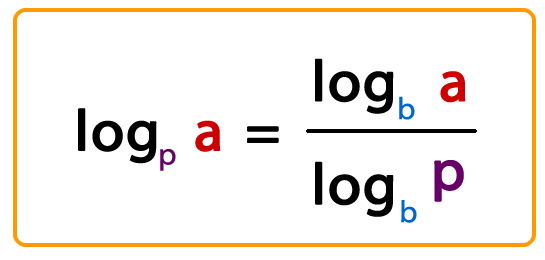
Ej:
log2 5 = log 5 / log 2
Más información de propiedades de los logaritmos
1.2. Ecuaciones logarítmicas
Resolución de ecuaciones logaritmicas
Ejm 1:
Ejem 2:
Ejem 3:
Ejem 4:
2. Propiedades exponenciales
Propiedades exponenciales
2.1. Ecuaciones exponenciales
Ecuaciones exponenciales,ejercicios detallados
3. Sistemas de ecuaciones exponenciales y logarítmicas.
Ecuaciones exponenciales y logarítmicas
Ejm:1
Ejm:2
4. Representación gráfica de una función exponencial y logarítmica
Graficando funciones exponenciales
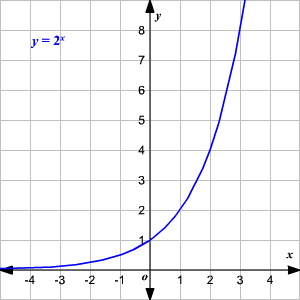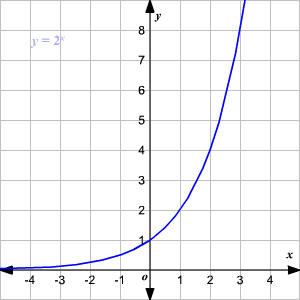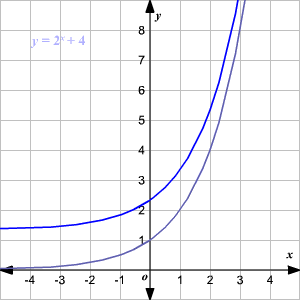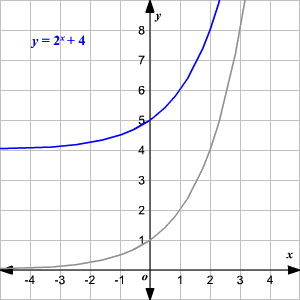
Una función exponencial sencilla para graficar es ![]()
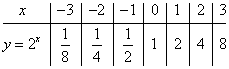
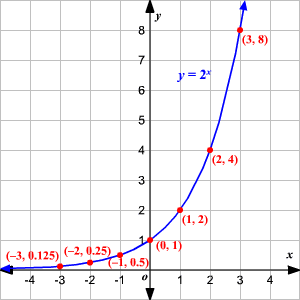
Dese cuenta que la gráfica tiene al eje de las x como una asíntota en la izquierda, y aumenta muy rápido en la derecha.
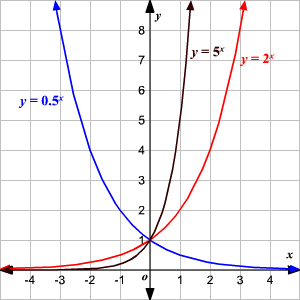
Cambiar la
base
cambia la forma de la gráfica.
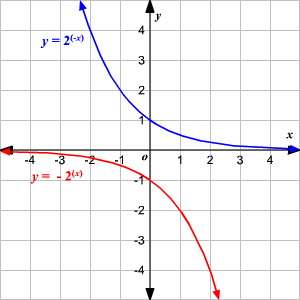
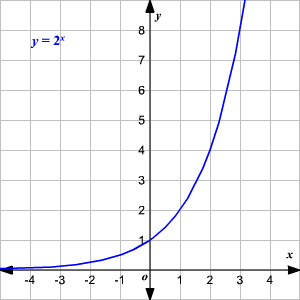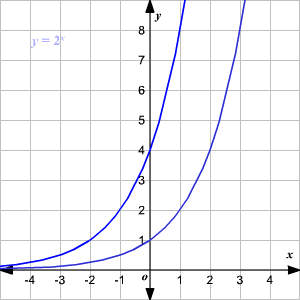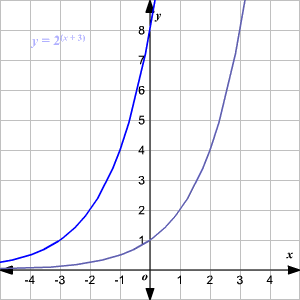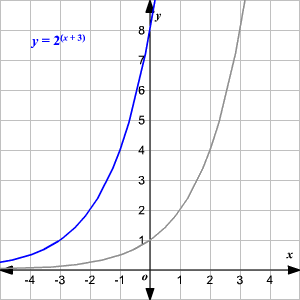
Reemplazando x con el reflejo de – x la gráfica atraviesa el eje de las y ; reemplazando y con - y se refleja a través del eje de las x .
Reemplazando x con x + h se traduce la gráfica a h unidades a la izquierda.
Reemplazando y con y - k (que es lo mismo que sumar k en el lado derecho) se traduce la gráfica k unidades hacia arriba.
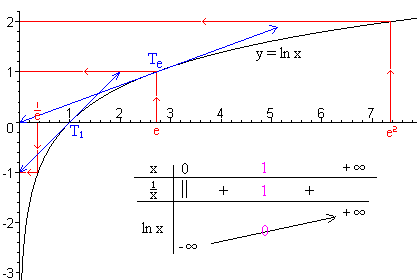
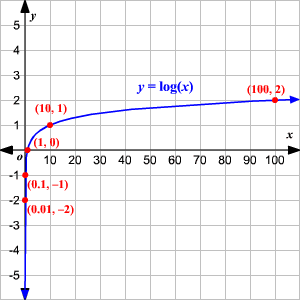
Graficando funciones logarítmicas
La función ![]() es la
función inversa
de
es la
función inversa
de ![]()
Así, es la reflexión de esa gráfica a través de la recta diagonal y = x .
Cuando no se escribe la base, asuma que el log es base 10.
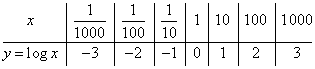
Video de grafica de una función logaritmica
Video de una grafica de función exponencial
5. Aplicación de funciones exponenciales y logarítmicas en actividades diversas.
Aplicación de funciones exponenciales y logarítmicas a la vida cotidiana
Ver más ......