Imprimir libroImprimir libro

INECUACIONES Y NÚMEROS COMPLEJOS

Sitio: ue.aprendiendomas.com.bo
Curso: 4° - Matemáticas
Libro: INECUACIONES Y NÚMEROS COMPLEJOS
Impreso por: Invitado
Fecha: domingo, 24 de noviembre de 2024, 12:49

Tabla de Contenidos

1. Desigualdades e inecuaciones

Desigualdades e inecuaciones


solución de desigualdades


Intervalos como solución de una inecuación





1.1. Inecuaciones de primer y segundo grado

Sistemas de inecuaciones con una incógnita de primer y segundo grado

A continuación te voy a explicar cómo resolver sistemas de inecuaciones lineales o de primer grado con una incógnita, así como sistemas de inecuaciones de segundo grado con una incógnita.

Lo veremos con ejercicios resueltos paso a paso.

¡Empezamos!

Solución de un sistema de ecuaciones con una incógnita

Tal y como explico en el Curso de Inecuaciones, una inecuación con una incógnita tiene como solución un rango de valores.

Pues bien.

En un sistema de inecuaciones con una incógnita, la solución estará formada por el rango de valores en el cual se solapen cada una de las soluciones de las inecuaciones que forman el sistema.

Cualquier valor que se encuentre dentro de ese intervalo cumplirá las desigualdades de todas las inecuaciones.

Si no hay ningún rango de valores donde se solapen todas las soluciones, el sistema no tendría solución.

Lo verás más claro cuando vayamos resolviendo ejercicios.

Para poder resolver un sistema de inecuaciones de primer y segundo grado con una incógnita, es necesario que sepas resolver por separado inecuaciones de primer grado como inecuaciones segundo grado.

Vamos a empezar por resolver sistemas de ecuaciones de primer grado con una incógnita.

Cómo resolver sistemas de ecuaciones lineales de primer grado con una incógnita

Los sistemas de inecuaciones lineales de primer grado con una incógnita son aquellos donde todas las inecuaciones que forman el sistema son inecuaciones de primer grado, como por ejemplo:


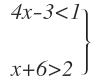
Para resolver este sistema, tenemos que resolver por separado cada inecuación y después, el rango de valores donde coincidan ambas soluciones será la solución del sistema.

Empezamos resolviendo la primera inecuación:



Pasamos el 3 sumando al segundo miembro:

Operamos en el segundo miembro:

Y pasamos el 4 dividiendo al segundo miembro:

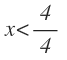
Volvemos a operar y llegamos a su solución:

Los valores de x que sean menores que 1, o el intervalo (-∞,1), que si lo representamos en al recta, queda de la siguiente mantera:

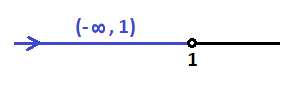
Seguimos resolviendo la segunda inecuación:

Y operamos:


La solución de esta inecuación son los valores de x que sean mayores que -4, o lo que es lo mismo el intervalo (-4,∞)


Una vez tenemos ambas soluciones por separado, representamos ambas soluciones juntas en la recta. El intervalo donde se solapen ambas soluciones será la solución del sistema:


En nuestro caso es el intervalo (-4,1):



Cómo resolver sistemas de ecuaciones de segundo grado con una incógnita


Los sistemas de inecuaciones de segundo grado con una incógnita son aquellos donde al menos una de las inecuaciones que forman el sistema es una inecuación de segundo grado.

Por ejemplo:

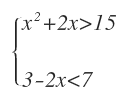
Vamos a ver cómo resolver este sistema. El procedimiento es el mismo que en el caso anterior, solo que ahora tenemos una inecuación de segundo grado y por tanto, se resuelve de una forma distinta  a las de primer grado.

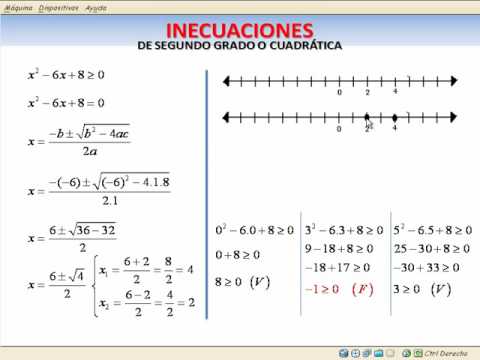
Empezamos resolviendo la primera inecuación, que se trata de una inecuación de segundo grado:

Pasamos el 15 al primer miembro:

Y resolvemos la ecuación de segundo grado que resulta al cambiar la desigualdad por el signo igual:


Cuyas soluciones son:

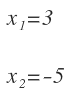
Las representamos en la recta real:



Y ahora tenemos que saber en qué tramos se cumple que es mayor que cero.

Le doy un valor a la x entre el -3 y 5 y veo que el resultado es negativo:

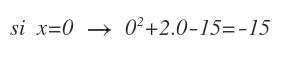
Luego en los otros 2 tramos será positivo:


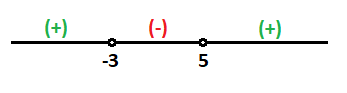
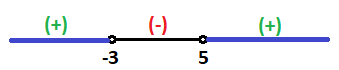
Por tanto, la solución de esta inecuación son los tramos donde la ecuación es positiva, que los marco en azul:

Por tanto, la solución de la inecuación de segundo grado es:

Es decir, los valores de x que sean menores que -3 y mayores que 5.

Ahora vamos a resolver la segunda inecuación:

En este caso es una inecuación de primer grado.

Pasamos el -2 dividiendo al segundo miembro y como es negativo, la damos la vuelta a la desigualdad:

Y finalmente nos queda:

La solución son los valores de x mayores que -2 o los que pertenecen al intervalo (-2,∞).

Representado en la recta real es:

Ya tenemos la solución de cada inecuación por separado.

Ahora tenemos que encontrar el rango de valores donde se solapen las dos soluciones.

Para ello, en la recta, dibujamos las dos soluciones, una encima de la otra:

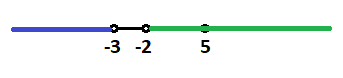
El tramo donde se solapan la línea azul (solución de la primera inecuación) y la línea verde (solución de la segunda inecuación) es el tramo rojo:

Por lo que la solución del sistema es desde 5 hasta infinito, sin coger el 5, ya que es solución de la primera inecuación pero de la segunda no:


Cualquier valor que se sea mayor que 5 cumplirá las dos desigualdades del sistema.

 Más sobre inecuaciones de Primer Grado


Inecuaciones de Segundo Grado (Cuadráticas)













1.2. Inecuaciones de segundo grado con valor absoluto

Inecuaciones de segundo grado con valor absoluto




Más información sobre inecuaciones cuadraticas con valor absoluto


1.3. Inecuaciones de grado superior a 2

Inecuaciones polinómicas de grado superior a dos

Son inecuaciones que se pueden escribir de la forma:  an xn  + an-1 xn-1 + …….. + a1 x + a0 > 0

Para su resolución, se procede de forma similar al caso de las inecuaciones polinómicas de segundo grado, es decir, se factoriza el polinomio y se estudia su signo.

Para resolver una inecuación polinómica , seguiremos los siguientes pasos:

  1. Escribir la inecuación en la forma general, es decir, realizar las operaciones necesarias para que todo la expresión polinómica quede a un lado de la inecuación y cero en el otro lado.
  2. Factorizar el polinomio. Si no se puede factorizar, encontrar los puntos donde el polinomio es igual a cero.
  3. Hallar los intervalos de prueba. Esto se logra determinando los valores en que cada factor es cero, estos puntos determinarán los límites de los intervalos en la recta numérica.
  4. Seleccionar un punto de prueba en cada intervalo para determinar el signo en cada intervalo.

La solución la conforman todos los intervalos que hacen que la desigualdad sea cierta. La solución se puede expresar algebraica (como intervalo) y gráficamente.

Ejemplo:

Factorizamos la inecuación:

(x -1)(x – 2)(x – 1/2)(x + 2/3) < 0

En la que inter las raíces:

x = 1   ,    x = 2  ,   x = 1/2  ,   x =- 2/3

Estudiamos el signo en los intervalos:

El conjunto solución es:    (-2/3 ,1/2) ∪ (1 , 2)

Ver más sobre inecuaciones de grado superior a 2








1.4. Sistemas de inecuaciones de primer y segundo grado

Inecuaciones y sistemas de inecuaciones de primer grado

Una inecuación es como una ecuación, con la diferencia de que cada uno de los dos miembros que la componen no está separado por el signo =

Sino por una desigualdad. Las desigualdades son cuatro: mayor >, menor <, mayor o igual ≥ y menor o igual ≤

No vamos a entrar aquí en un estudio exhaustivo de las propiedades de las desigualdades ni de las relaciones de orden en el conjunto de los números reales. Solamente destacaremos que las desigualdades se comportan como las igualdades para la operación suma pero de manera algo distinta para la operación producto.

Si sumamos (o restamos) la misma cantidad en los dos miembros de una desigualdad, la desigualdad no varía. En el caso de una inecuación obtenemos una inecuación equivalente. Igual ocurre con el producto si multiplicamos (o dividimos) los dos miembros de una desigualdad por la misma cantidad positiva: la desigualdad no varía. Sin embargo, si multiplicamos (o dividimos) los dos miembros de una inecuación por una misma cantidad negativa, la desigualdad cambia de sentido. Así pues, cuando manipulemos inecuaciones y multipliquemos o dividamos ambos miembros por la misma cantidad obtendremos inecuaciones equivalentes, pero tendremos cuidado cuando lo hagamos con una cantidad negativa pues en ese caso la inecuación equivalente a la anterior tendrá cambiado el sentido de la desigualdad. Mejor lo vemos con un ejemplo.

Resolvamos la siguiente inecuación de primer grado:

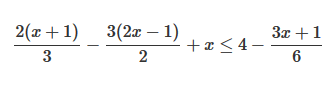
Se procede exactamente igual que en una ecuación de primer grado (eliminamos paréntesis y denominadores, trasponemos términos y reducimos términos semejantes). En este caso multiplicamos todos los términos (los dos miembros de la desigualdad) por , que es el mínimo común múltiplo de los denominadores y luego procedemos a ir simplificando hasta obtener una desigualdad completamente reducida.Veámoslo:

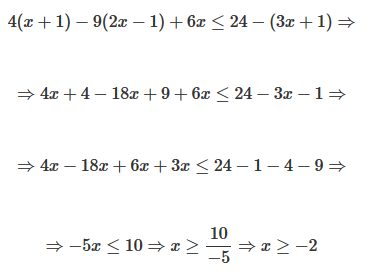
Obsérvese que, en el penúltimo paso, al dividir los dos miembros de la desigualdad entre −5, la desigualdad cambia de sentido. La solución de la inecuación, x≥−2, se puede escribir en forma de intervalo. En este caso la solución se corresponde con todos los números reales mayores o iguales que −2, es decir, el intervalo de números reales [−2, +∞). Obsérvese que este intervalo es cerrado por la izquierda (se denota con un corchete) pues la desigualdad, al tener el igual (no estricta), incluye al número −2

Para la representación gráfica de la solución trazamos, sobre la recta real, una flecha comenzando en −2
con sentido hacia la derecha, para significar que estamos tomando todos los números reales mayores que −2. Como se ha de incluir el extremo, el “circulito” que hace de origen de la flecha, lo “rellenamos”. De esta forma cerramos el intervalo incluyendo el extremo (en este caso −2).


Si lo que tenemos que resolver es un sistema lineal de dos o más inecuaciones con una incógnita, el procedimiento a seguir es resolver cada una de las inecuaciones por separado. Una vez hecho esto se representa gráficamente la solución de cada una de ellas. La parte simultánemente común de cada una de las soluciones es la solución del sistema. Si no hay parte común el sistema de inecuaciones no tiene solución. Veamos un ejemplo.

Resolveremos el siguiente sistema de inecuaciones:

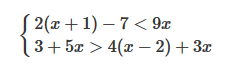
Para ello resolvemos en primer lugar la primera inecuación:

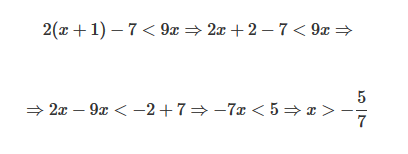
A continuación resolvemos la segunda inecuación:

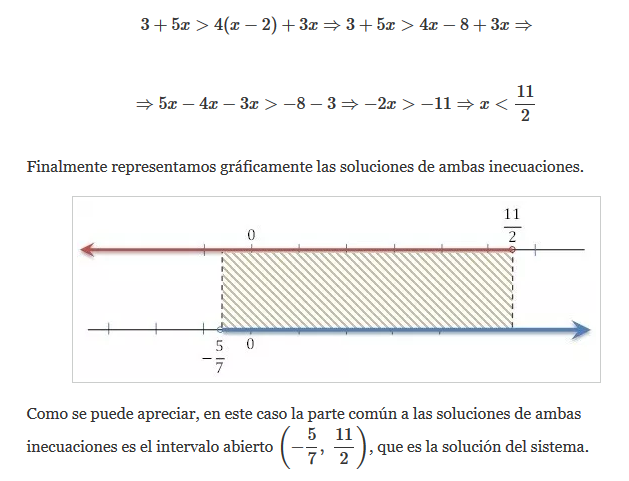
Ver más sobre sistemas de inecuaciones de segundo grado




2. Números complejos

Números Complejos

Los números complejos son aquellos que resultan de la suma de un número real y un número imaginario; entendiéndose como número real, aquel que puede expresarse de forma entera (s, 10, 300, etc.) o decimal (2,24; 3,10; etc.), mientras que el imaginario es aquel número cuyo cuadrado es negativo. Los números complejos son muy utilizados en el álgebra y en el análisis, además de aplicarse en otras especialidades de las matemáticas puras como lo son el cálculo de integrales, ecuaciones diferenciales, en la hidrodinámica, la aerodinámica, entre otras.


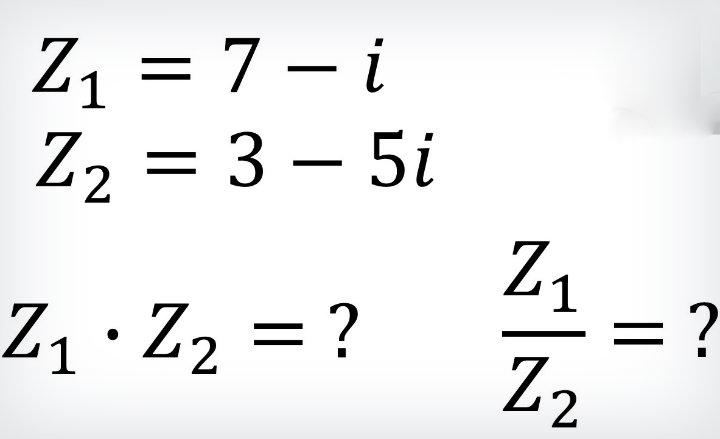
En las matemáticas, estos números representan un grupo que son considerados como puntos del plano y que se les conoce como el plano complejo. Este grupo incluye a los números reales y a los imaginarios. Una característica resaltante de estos números es el teorema fundamental del álgebra, el cual manifiesta que cualquier ecuación algebraica de grado “n” tendrá específicamente “n” soluciones complejas.

El concepto de números complejos surge ante la imposibilidad de los números reales de incluir a las raíces de orden par, del grupo de números negativos. Por lo tanto, los números complejos tienen la capacidad de mostrar todas las raíces de los polinomios, cosa que no pueden hacer los números reales.

Como ya se ha mencionado, los números complejos suelen usarse en diversas ramas de las matemáticas, física e ingeniería y es que gracias a sus características tienen la capacidad de representar las ondas electromagnéticas y la corriente eléctrica. En la electrónica y en las telecomunicaciones, es frecuente el uso de los números complejos.

Según registros históricos, el matemático griego Herón de Alejandría, fue uno de los primeros en plantear la aparición de los números complejos, esto debido a las dificultades que surgieron al momento de construir una pirámide. Pero no fue sino hasta el siglo XVl, cuando los números complejos comenzaron a ocupar un lugar significativo dentro de las ciencias. Es importante resaltar que para ese entonces se buscaban fórmulas que permitieran la obtención de raíces exactas de los polinomios de nivel 2 y 3. Por lo tanto su interés era el de hallar las raíces reales de las ecuaciones que se mencionaron anteriormente, así como también luchar con las raíces de cifras negativas.

Por último, si se desea analizar geométricamente los números complejos, es necesario utilizar un plano complejo; entendiéndose este como un plano cartesiano modificado en donde la parte real se encuentra en el eje de las abscisas, mientras que los imaginarios se ubican en el eje de ordenadas.

Ver más sobre números complejos o imaginários






2.1. La unidad imaginaria

La unidad imaginaria

La unidad imaginaria es el número y se designa por la letra i.

Potencias


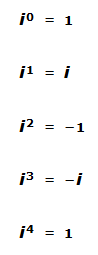
Los resultados se repiten de cuatro en cuatro, por eso, para saber cuánto vale una determinada potencia de i, se divide el exponente entre 4, y el resto es el exponente de la potencia equivalente a la dada.

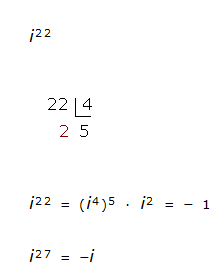
Más información sobre números imaginarios




2.2. Expresión binómica de los números complejos

Expresión binómica de los números complejos

Forma binómica

Un número complejo Z (no confundirse con C, que es el conjunto al que pertenecen) se puede representar de la forma:


Perteneciendo a y b al conjunto de los números reales.

Esta forma de escribir los números complejos corresponde a la forma binómica, que tiene dos partes:

  • a = Parte real
  • b = Parte imaginaria

Éstos son ejemplos de números complejos en forma binómica:

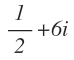
Si la parte real de un número complejo es 0, ese número es imaginario puro, ya que solo tiene parte imaginaria:

Por otro lado, si no tiene parte imaginaria, estamos hablando de un número real puro, que no es ni más ni menos que un número real:

Más información sobre números complejos en forma binómica





2.3. Propiedades de los números complejos

Propiedades de los números complejos

El sistema de números complejos, construido a partir de los números reales, tienen propiedades heredadas de éstos como las propiedades sobre la suma y la multiplicación.
Recuerde que dos números complejos, z1=a1+b1i   y   z2=a2+b2i son iguales si y sólo si son iguales sus partes reales y sus partes imaginarias, a1=a2   y   b1=b2.
Una idea para demostrar muchas de las propiedades sobre identidades sobre operaciones de suma y multiplicación es efectuar las operaciones de un miembro de la identidad, aplicar las propiedades de los números reales a las partes reales y a las partes imaginarias para llegar al lado derecho de la identidad. De aquí decimos que las propiedades de la suma y la multiplicación son heredadas de las propiedades de los números reales.
Pero el sistema de los números complejos no tiene todas las propiedades de los números reales, por ejemplo no se tienen propiedades de orden.
En la página se enuncian otras propiedades propias del sistema de números complejos junto con algunas pruebas.



Propiedades de la suma
Se define la suma de dos números complejos z1=a+bi y z2=c+di como

(a+bi)+(c+di)=(a+c)+(b+d)i

A partir de esta definición, usando las propiedades de los números reales, podemos probar que se cumplen las siguientes.

Propiedad de cierre o cerradura para la suma
          Para z1,z2∈C se tiene que z1+z2∈C

Propiedad conmutativa
Para cualesquiera z1,z2∈C se cumple que
z1+z2=z2+z1

Propiedad asociativa
Para cualesquiera z1,z2,z3∈C se cumple que
(z1+z2)+z3=z1+(z2+z3)

Propiedades de la multiplicación
 Se define el producto de dos números complejos z1=a+bi   y   z2=c+di como

(a+bi)⋅(c+di)=(ab−bd)+(ad+bc)i

A partir de esta definición, usando las propiedades de los números reales, podemos demostrar que se cumplen las siguientes. Las pruebas son similares a las de la suma.

Propiedad de cierre o cerradura para la multiplicación
          Para z1,z2∈C se tiene que z1⋅z2∈C

Propiedad conmutativa
Para cualesquiera z1,z2∈C se cumple que
z1⋅z2=z2⋅z1

Propiedad asociativa
Para cualesquiera z1,z2,z3∈C se cumple que
(z1⋅z2)⋅z3=z1⋅(z2⋅z3)

Existencia del elemento neutro para la multiplicación
1+0i, abreviado por 1, es el elemento neutro para la multiplicación.

Existencia del inverso multiplicativo o recíproco
Todo número complejo z, dintinto de 0, tiene un único inverso multiplicativo , denotado por z−1



Propiedades del conjugado
 El conjugado de un número complejo z=a+bi, denotado por z¯¯¯, se define como z¯¯¯=a−bi

Es claro las siguientes
El conjugado de un número real es él mismo.

El conjugado de un número imaginario puro es el opuesto del número.
A continuación otras propiedades del conjugado

El conjugado del conjugado
Para z∈C se tiene que

z¯¯¯¯¯¯=z


La suma y resta con el conjugado
Para z∈C se tiene que

z+z¯¯¯=2Re(z) y z−z¯¯¯=2Im(z)

El producto con el conjugado
Para cualesquiera z∈C, z=a+bi, se tiene que
z⋅z¯¯¯=a2+b2




Más información sobre números complejos y sus propiedades





PROPIEDADES DE
LOS NÚMEROS COMPLEJOS


El sistema de números complejos, construido a partir de los números reales, tienen propiedades heredadas de éstos como las propiedades sobre la suma y la multiplicación.
Recuerde que dos números complejos, z1=a1+b1i   y   z2=a2+b2i son iguales si y sólo si son iguales sus partes reales y sus partes imaginarias, a1=a2   y   b1=b2.
Una idea para demostrar muchas de las propiedades sobre identidades sobre operaciones de suma y multiplicación es efectuar las operaciones de un miembro de la identidad, aplicar las propiedades de los números reales a las partes reales y a las partes imaginarias para llegar al lado derecho de la identidad. De aquí decimos que las propiedades de la suma y la multiplicación son heredadas de las propiedades de los números reales.
Pero el sistema de los números complejos no tiene todas las propiedades de los números reales, por ejemplo no se tienen propiedades de orden.
En la página se enuncian otras propiedades propias del sistema de números complejos junto con algunas pruebas.





Propiedad transitiva
 Si z1=z2 y z2=z3 entonces z1=z3
Sean z1=a1+b1i, z2=a2+b2i y z3=a3+b3i,

Tenemos que ver que las partes reales de z1 y z3 son iguales.

Por la igualdad de los números complejos se tiene
Si z1=z2 entonces a1=a2   y   b1=b2
Si z2=z3 entonces a2=a3   y   b2=b3

Entonces por la propiedad transitiva de los números reales como a1=a2   y  a2=a3 se cumple que a1=a3

De manera similar, llegamos que b1=b3.

Así conluimos que z1=z3.



Propiedades de la suma
 Se define la suma de dos números complejos z1=a+bi y z2=c+di como
(a+bi)+(c+di)=(a+c)+(b+d)i

A partir de esta definición, usando las propiedades de los números reales, podemos probar que se cumplen las siguientes.

Propiedad de cierre o cerradura para la suma
          Para z1,z2∈C se tiene que z1+z2∈C

Propiedad conmutativa
Para cualesquiera z1,z2∈C se cumple que
z1+z2=z2+z1

Propiedad asociativa
Para cualesquiera z1,z2,z3∈C se cumple que
(z1+z2)+z3=z1+(z2+z3)
Sean z1=a1+b1i, z2=a2+b2i y z3=a3+b3i,


Desarrollamos el lado izquierdo, primero sustituímos
((a1+b1i)+(a2+b2i)) + (a3+b3i)

      Aplicamos la suma de complejos planteada entre paréntesis

=((a1+a2)+(b1+b2)i)+(a3+b3i)

      Sumamos

=((a1+a2)+a3)+((b1+b2)+b3)i

      Aplicamos la propiedad asociativa en la parte real y en la parte imaginaria
=(a1+(a2+a3))+(b1+(b2+b3))i

Siguiendo el mismo proceso podemos demostrar que la última línea es igual a z1+(z2+z3).


Existencia del elemento neutro para la suma
0+0i, abreviado por 0, es el elemento neutro para la suma.


Existencia del inverso aditivo u opuesto
Todo número complejo z tiene un único inverso aditivo, denotado por −z.
Esta propiedad se refiere a la existencia, para cada número real z, de un único número complejo −z, tal que z+(−z)=0

El opuesto de z=a+bi es el número complejo −a−bi Efectivamente, si z=a+bi, se tiene que
z+(−z)====(a+bi)+(−a−bi)(a+(−a))+(b+(−b))i0+0i0
y es único, si z~=c+di es un opuesto de z, se tiene
(a+bi)+(c+di)=0+0i
Esto es
(a+c)+(b+d)i=0+0i
Pero sabemos que dos números complejos son iguales si son iguales sus partes reales y sus partes imaginarias. De aquí, a+c=0 y b+d=0. Ahora estamos en los números reales, de aquí c=−a   y   d=−b. Es decir, hay un único inverso dado por −a−bi





Propiedades de la multiplicación
 Se define el producto de dos números complejos z1=a+bi   y   z2=c+di como
(a+bi)⋅(c+di)=(ab−bd)+(ad+bc)i

A partir de esta definición, usando las propiedades de los números reales, podemos demostrar que se cumplen las siguientes. Las pruebas son similares a las de la suma.

Propiedad de cierre o cerradura para la multiplicación
          Para z1,z2∈C se tiene que z1⋅z2∈C

Propiedad conmutativa
Para cualesquiera z1,z2∈C se cumple que
z1⋅z2=z2⋅z1

Propiedad asociativa
Para cualesquiera z1,z2,z3∈C se cumple que
(z1⋅z2)⋅z3=z1⋅(z2⋅z3)

Existencia del elemento neutro para la multiplicación
1+0i, abreviado por 1, es el elemento neutro para la multiplicación.

Existencia del inverso multiplicativo o recíproco
Todo número complejo z, dintinto de 0, tiene un único inverso multiplicativo , denotado por z−1.   Leer más


Propiedad distributiva
 Para cualesquiera z1,z2,z3∈C se cumple que
z1⋅(z2+z3) = z1⋅z2+z1⋅z3


2.4. Operaciones de números complejos (adición, sustracción, multiplicación y división)

Operaciones con números complejos