MEDICIONES Y ERRORES EN LA INVESTIGACIÓN COMUNITARIA

Sitio:	ue.aprendiendomas.com.bo
Curso:	2° - Ciencias Naturales
Libro:	MEDICIONES Y ERRORES EN LA INVESTIGACIÓN COMUNITARIA

Impreso por:	Invitado
Fecha:	sábado, 23 de noviembre de 2024, 15:02

Tabla de Contenidos

1. Cálculo de Errores de los instrumentos de medición de uso cotidiano en la comunidad
- 1.1. ERROR ABSOLUTO Y ERROR RELATIVO
2. Diferencia entre precisión y exactitud
- 2.1. ¿Cuál es la diferencia entre exactitud y precisión?
3. Determinación de la magnitud del error en las mediciones
- 3.1. Qué es el error absoluto y el error relativo
4. *Medidas utilizadas por las naciones y pueblos indígena originarios.

1. Cálculo de Errores de los instrumentos de medición de uso cotidiano en la comunidad

En nuestras actividades cotidianas, o en las que se realizan en la industria o la investigación, siempre se busca realizar las mediciones con cuidado, procurando que los instrumentos o aparatos empleados ésten calibrados y proporcionen resultados confiables. Sin embargo, hay que tener presente que cuando se mide una magnitud Física, el valor que se obtiene no sera exactamente igual al valor verdadero de dicha magnitud, por mas que se realice con el mayor cuidado y se utilicen aparatos recíen calibrados y de gran presición. Por lo tanto se puede decir que en las mediciones no existe una medida exacta, ya que es imposible medir el valor de una magnitud sin impresición alguna. Por ello es muy importante determinar que tan cercano es el resultado obtenido al valor verdadero o valor real. Para lograrlo, se lleva acabo el llamado análisis de error.

Instrumentos de medida: Sensibilidad, precisión, incertidumbre.

La parte fundamental de todo proceso de medida es la comparación de cierta cantidad de la magnitud que deseamos medir con otra cantidad de la misma que se ha elegido como unidad patrón. En este proceso se utilizan los instrumentos de medida que previamente están calibrados en las unidades patrón utilizadas (ver Centro Español de Metrología).

Los instrumentos de medida nos permiten realizar medidas directas (un número seguido de la unidad) de una magnitud.

Un instrumento de medida se caracteriza por los siguientes factores:

Sensibilidad. Es la variación de la magnitud a medir que es capaz de apreciar el instrumento. Mayor sensibilidad de un aparato indica que es capaz de medir variaciones más pequeñas de la magnitud medida.
Precisión. La medida que es capaz de apreciar un instrumento. Está relacionada con la sensibilidad. A mayor sensibilidad, menores variaciones es capaz de apreciar, medidas más pequeñas nos dará el instrumento.

Un instrumento de medida debe ser capaz de medir la cifra más pequeña de su escala.

La incertidumbre está relacionada con el proceso de medida. Se trata del máximo error de la medida. Evidentemente, está relacionada con la precisión del instrumento. Por regla general se toma como incertidumbre la precisión del aparato, algunas veces aunque no sea demasiado correcto se toma la mitad de la precisión como incertidumbre.

Errores experimentales.

Tenemos dos tipos de errores en el proceso de medida:

Errores sistemáticos. Tienen que ver con la metodología del proceso de medida (forma de realizar la medida):

Calibrado del aparato. Normalmente errores en la puesta a cero. En algunos casos errores de fabricación del aparato de medida que desplazan la escala. Una forma de arreglar las medidas es valorando si el error es lineal o no y descontándolo en dicho caso de la medida.
Error de paralaje: cuando un observador mira oblicuamente un indicador (aguja, superficie de un líquido,...) y la escala del aparato. Para tratar de evitarlo o, al menos disminuirlo, se debe mirar perpendicularmente la escala de medida del aparato.

Errores accidentales o aleatorios. Se producen por causas difíciles de controlar: momento de iniciar una medida de tiempo, colocación de la cinta métrica, etc. Habitualmente se distribuyen estadísticamente en torno a una medida que sería la correcta. Para evitarlo se deben tomar varias medidas de la experiencia y realizar un tratamiento estadístico de los resultados. Se toma como valor o medida más cercana a la realidad la media aritmética de las medidas tomadas.

Ejemplo. Se mide la distancia entre dos puntos y se obtienen como resultados 4,56 m; 4,57 m; 4,55 m; 4,58 m; 4,55 m. Si calculamos la media aritmética (sumamos todas las medida y dividimos por el total de medidas, cinco en este caso) nos sale 4,562 m. Como el aparato no sería capaz de medir milésimas, redondeamos y nos queda 4,56 m como medida que tomamos como real.

Cálculo de errores: error absoluto, error relativo.

Bien sea una medida directa (la que da el aparato) o indirecta (utilizando una fórmula) existe un tratamiento de los errores de medida. Podemos distinguir dos tipos de errores que se utilizan en los cálculos:

Error absoluto. Es la diferencia entre el valor de la medida y el valor tomado como exacto. Puede ser positivo o negativo, según si la medida es superior al valor real o inferior (la resta sale positiva o negativa). Tiene unidades, las mismas que las de la medida.
Error relativo. Es el cociente (la división) entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto por ciento (%) de error. Al igual que el error absoluto puede ser positivo o negativo (según lo sea el error absoluto) porque puede ser por exceso o por defecto. no tiene unidades.

CÁLCULO DE ERRORES. ERROR ABSOLUTO Y RELATIVO.

Fuente: http://www.mclibre.org/otros/daniel_tomas/diversificacion/matematicas/Calculo_de_errores.pdf

1.1. ERROR ABSOLUTO Y ERROR RELATIVO

2. Diferencia entre precisión y exactitud

La precisión y la exactitud son dos factores importantes, pero diferentes, que hay que considerar cuando se toman mediciones de datos. Tanto la exactitud como la precisión reflejan cuán cerca está una medición de un valor real, pero tienen ciertos matices que los diferencian.

Precisión vs Exactitud

La precisión es la consistencia de los resultados cuando se repiten las mediciones.
La exactitud refleja cuán cerca está una medición de un valor conocido o aceptado.

Precisión

La precisión es la consistencia de los resultados cuando se repiten varias mediciones. Cuanto menor sea la dispersión de las mediciones mayor será la precisión.

Exactitud

En general, en matemáticas y en ciencias, nos referimos a la exactitud como lo cerca que está una medida de su valor real.

Sin embargo, hay algunos organismos como la ISO (Organización Internacional de Estandarización) que define la exactitud como “mediciones con resultados tanto verdaderos como consistentes”. Lo que significa que para la ISO una medida “exacta” tiene que ser exacta y precisa.

Uno de los ejemplos más fáciles es de una balanza.

Imagina que vamos a medir una masa que pesa 50.0 gramos y nuestra balanza marca en sucesivas mediciones: 51,1, 51,0, 51,2 y 51,1. Esta balanza será bastante precisa pero no muy exacta, habrá que calibrarla.

Si realizamos lo mismo y obtenemos los valores de: 49,0, 51,0, 50,5, 49,5. Esta balanza será mucho más exacta (la media de los valores se aproxima más), sin embargo, es menos fiable (menos precisa).

Otro ejemplo muy visual es el de la puntería.

Imagina por ejemplo que tenemos un arma colocada sobre un soporte fije y disparamos a una diana.

Si los disparos siempre van hacia el mismo sitio y se encuentran agrupados, podemos decir que el arma tiene una buena precisión.
Si a su vez añadimos que todos los disparos dan en la diana, tendremos buena precisión (agrupados) y buena exactitud (cerca del objetivo).

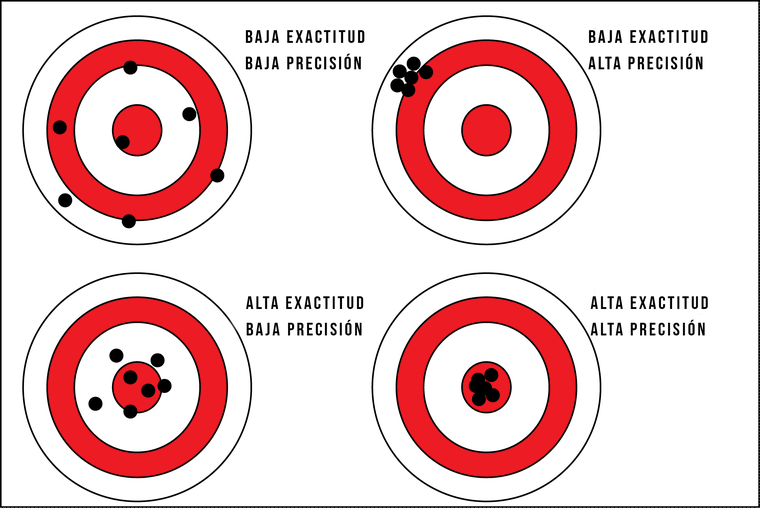
¿Qué crees que es mejor?

Que nos pesemos en una báscula tres veces y cada número es diferente, pero cercano al peso real (báscula exacta).
Que nos pesemos tres veces en una báscula y todos los valores estén muy próximos entre sí, pero alejados del peso real (báscula precisa).

Pues dependerá de nuestro objetivo. Si queremos comprobar cuánto pesamos preferiremos la báscula exacta, pero si estamos a dieta y queremos ver la evolución de nuestro peso, nos servirá mejor una báscula precisa.

Y ahí es donde entra la calibración de los aparatos que pretende mejorar la exactitud de un aparato preciso.

Por eso, tenemos que tener claro que la tanto la precisión como la exactitud son necesarias; y más en el ámbito científico, lo cual no siempre es fácil. Y es que, siempre hay errores, otro concepto muy importante.

Un error es la diferencia entre el valor real y el medido. Sin embargo, debido a que el valor real nunca es conocido con veracidad (es lo que intentamos medir), el error siempre debe ser estimado.

Resumen

Como son dos términos tan relacionados es muy fácil intercambiarlos, pero la siguiente regla mnemotécnica te ayudará a recordarlos:

La pRecisión es Repetición de los resultados.
La eXactitud es dar en la X de la diana (o casi).

2.1. ¿Cuál es la diferencia entre exactitud y precisión?

3. Determinación de la magnitud del error en las mediciones