IGUALDAD, DESIGUALDAD y ESTADÍSTICA EN LA MATEMÁTICA.
| Sitio: | ue.aprendiendomas.com.bo |
| Curso: | 2° - Matemáticas |
| Libro: | IGUALDAD, DESIGUALDAD y ESTADÍSTICA EN LA MATEMÁTICA. |
| Impreso por: | Invitado |
| Fecha: | lunes, 7 de abril de 2025, 11:55 |
Tabla de Contenidos
- 1. Ecuaciones de 1er grado con una incógnita y su aplicación en actividades económicas de diversos ámbitos
- 2. Inecuaciones de primer grado: planteamiento y resolución de inecuaciones de 1er con una incógnita relacionada a actividades económicas de diversos ámbitos.
- 3. Función lineal y afín, su expresión y representación gráfica.
- 4. Probabilidad de un suceso y la regla de Laplace
- 5. Diagrama del árbol
1. Ecuaciones de 1er grado con una incógnita y su aplicación en actividades económicas de diversos ámbitos
En cuanto a las matemáticas, las ecuaciones de primer grado son la introducción al álgebra. Su comprensión es imprescindible para cualquier tipo de ecuaciones: ecuaciones de segundo grado o de grado mayor, exponenciales, irracionales, etc. y para los sistemas de ecuaciones.
En cuanto a la vida real, aunque en un principio no se piense así, las ecuaciones son una herramienta de gran utilidad que nos permiten resolver numerosos problemas a los que nos enfrentamos diariamente. Podemos comprobarlo en la sección de problemas.
Como ya indica su nombre, en las ecuaciones de primer grado, la parte literal de los monomios no tiene exponente (por ejemplo, 3x puede formar parte de una ecuación pero 3x2 no porque sería de segundo grado). Justamente este hecho nos asegura que, en caso de existir solución, hay sólo una (excepto el caso especial en qué hay infinitas soluciones).
Decimos "en caso de existir solución" ya que en ocasiones las ecuaciones no tienen solución. Por ejemplo, la ecuación x = x + 1 (cuya lectura es "un número que es igual a su consecutivo") no tiene solución porque esto nunca se cumple. De hecho, la ecuación se reduce a 1 = 0, lo cual es imposible.
Si obtenemos una igualdad imposible, la ecuación no tiene solución.Ejemplo:
Si obtenemos la ecuación 1 = 0 , la ecuación inicial no tiene solución.
Si obtenemos una igualdad que siempre se cumple, cualquier valor es solución de la ecuación, es decir, la solución es todos los reales.
Ejemplo:
Si obtenemos la igualdad 0 = 0 , la solución es todos los reales:
Procedimiento para eliminar los paréntesis.
Cuando hay denominadores y queremos evitarlos, multiplicamos toda la ecuación por el mínimo común múltiplo de éstos.
De este modo, al simplificar, los denominadores desaparecen.
Para quitar los paréntesis, multiplicamos el coeficiente de delante del paréntesis por todos los elementos que contiene.
El coeficiente puede ser el signo menos (es decir, -1, entonces el contenido cambia de signo), el signo más (es decir, +1, el contenido no cambia) o un número positivo, negativo o una fracción (este número pasa a multiplicar todo el contenido del paréntesis, cambiando los signos en el caso de ser negativo).
Cuando tenemos paréntesis anidados, es decir, un paréntesis dentro de otro, los vamos quitando desde fuera hacia dentro. Es decir, primero quitamos el paréntesis exterior (multiplicando su contenido por su coeficiente) y después, quitamos los siguientes procediendo del mismo modo: desde el más exterior a los más interiores. En realidad, no es necesario seguir un orden a la hora de quitar los paréntesis, pero es recomendable seguirlo mientras estamos aprendiendo.
En esta sección se resuelven ecuaciones de primer grado cuya dificultad va aumentado: ecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros).Ecuación I.1: ecuación![]()
Pasamos las x's a un lado de la igualdad (izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
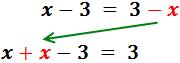
![]()
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
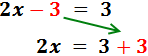
![]()
El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
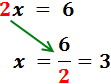
Por tanto, la solución de la ecuación es x = 3.
1.1. Resolución de ecuaciones de primer grado
2. Inecuaciones de primer grado: planteamiento y resolución de inecuaciones de 1er con una incógnita relacionada a actividades económicas de diversos ámbitos.
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad.
Los signos de desigualdad que se utilizan en las inecuaciones son: , , y :
a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3.
a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 > 2.
a ≤ b significa "a es menor o igual que b". Por ejemplo: 2 ≤ 2.
a ≥ b significa "a es mayor o igual que b". Por ejemplo: 3 ≥ 2.
Nota: se dice que los signos y son estrictos porque no puede darse la igualdad. Es decir, indican "menor" y "mayor", respectivamente, pero nunca "igual".
Solución de una inecuación
La solución de una inecuación es el valor o conjunto de valores que puede tomar la incógnita para que se cumpla la inecuación. A diferencia de las ecuación (cuyo signo es "="), no podemos saber de antemano el número de soluciones.
Puede darse el caso en que la solución es sólo un punto (por ejemplo, ), un intervalo (por ejemplo, ), una unión de intervalos o que no exista ninguna solución.
Tipos de inecuacionesInecuación lineal: cuando las expresiones de ambos lados son polinomios de primer grado.
Ejemplo:
La solución de esta inecuación es el intervalo .
Inecuación de segundo grado: cuando las expresiones de ambos lados son polinomios de grado menor o igual que 2.
Ejemplo:
Esta inecuación no tiene soluciones (reales) puesto que ningún número al cuadrado es negativo.
Inecuación racional: cuando las expresiones de uno o ambos lados son un cociente de polinomios.
Ejemplo:
La solución de esta inecuación es .
Inecuación con valor absoluto: cuando en las expresiones algebraicas hay valores absolutos.
Ejemplo:
Esta inecuación no tiene solución porque el módulo (valor absoluto) de un número es siempre mayor o igual que 0.
Resolvemos este tipo de inecuaciones en otra página:
La metodología de resolución es análoga a la de las ecuaciones, pero teniendo siempre en cuenta que se trata de una desigualdad. Esto supone, por ejemplo, cambiar el signo de desigualdad cada vez que multiplicamos o dividimos por un negativo para mantener la relación.
Ejemplo:
Para multiplicar por un negativo, por ejemplo, -2, cambiamos la desigualdad al resultado:
Notemos que si no la cambiamos, obtenemos una relación falsa ().
Intervalos: en los intervalos utilizaremos los símbolos "" y "" para el extremo izquierdo y los símbolos "" y "" para el extremo derecho. Los paréntesis indican que el extremo está incluido en el intervalo y los corchetes indican lo contrario.
Por ejemplo, el intervalo están incluido en el intervalo , pero también en y en . Sin embargo, el intervalo no está incluido en ni en .
Para expresar la unión de dos o más intervalos utilizamos el símbolo .
Inecuación 1
![]()
Solución
Agrupamos los monomios según su parte literal (los que tienen x y los que no) como hacemos en las ecuaciones de primer grado, pero sin multiplicar ni dividir toda la inecuación por un número negativo:
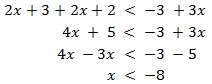
Por tanto, la solución es un intervalo:
![]()
donde los paréntesis indican que los extremos del intervalo no están incluidos (desigualdad estricta). Por ejemplo, los siguientes valores sí verifican la inecuación:
2.1. Inecuaciones de Primer Grado - Lineales | Ejemplo 1
2.2. Inecuaciones de Primer Grado - Ejercicios Resueltos
3. Función lineal y afín, su expresión y representación gráfica.
Función lineal
La función de variable real que tiene por ecuación general , cuya gráfica es una recta que pasa por el origen de coordenadas, se llama función lineal.
En las funciones lineales de este tipo , el valor de m, que corresponde a un número real, se llama pendiente. El pendiente mide la inclinación de la recta respecto del eje de abscisas.
Ejemplo
El pendiente de la recta es .
El pendiente de la recta es .
El pendiente de la recta es .
Es importante entender que como mayor es el valor del pendiente , mayor inclinación respecto el eje horizontal posee la recta. Además,
Si es positivo (), la recta pasa por el primer y por el tercer cuadrantes.
Si es negativo (), la recta pasa por el segundo y cuarto cuadrantes.
- Si es cero (), la recta es horizontal y coincide con el eje de abscisas.
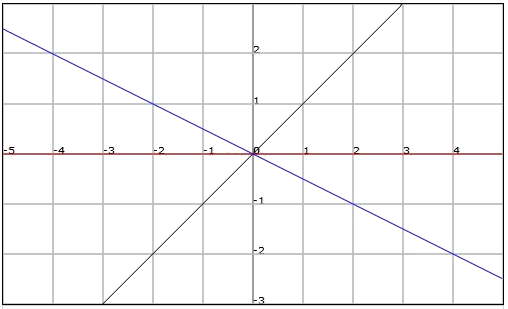
El pendiente de una recta también puede ser calculado a partir de las coordenadas de un punto de la recta para una función lineal, y de las coordenadas de dos puntos en general para una recta cualquiera.
3.1. Gráfica de la función lineal | Ejemplo 1
4. Probabilidad de un suceso y la regla de Laplace
Regla de Laplace
La regla de Laplace es tremendamente importante, puesto que nos permite calcular la probabilidad de un suceso, siempre que los sucesos elementales sean equiprobables, es decir, que todos los resultados posibles tengan la misma probabilidad. En estas condiciones, tenemos que:
- La probabilidad de un suceso se obtiene dividiendo el número de resultados que forman el suceso A entre el número de resultados posibles.
Si decimos que los sucesos de son los casos favorables a , entonces podemos escribir la regla de Laplace como:
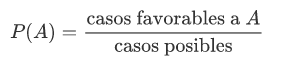
¡Atención! Debemos tener en cuenta que esta regla sólo funciona cuando todos los casos son equiprobables. NO es válido un razonamiento como el siguiente:
- Queremos calcular la probabilidad del suceso "ser atropellado por un tranvía". Sólo hay dos casos posibles, "ser atropellado" y "no ser atropellado". Hay un caso favorable, "ser atropellado". Por tanto, la probabilidad es de
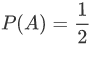
Esto significaría que cada vez que saliéramos a la calle, tendríamos el de probabilidad de ser atropellados. El error está, por supuesto, en que los dos sucesos no tienen la misma probabilidad.
Por este mismo motivo, si queremos resolver un problema con la regla de Laplace, tenemos que ir con cuidado si queremos considerar que nuestros resultados posibles están desordenados, puesto que podría ser que no todos fueran igual de probables. Veamos el siguiente ejemplo NO válido.
Si en una familia hay dos hijos, y suponemos que la probabilidad de ser hombre es la misma que la de ser mujer, ¿cuál es la probabilidad de que los dos hijos sean del mismo sexo?
Podríamos argumentar que el espacio muestral es
![]()
Entonces, los casos favorables son , y los casos posibles son , por lo que la probabilidad sería de .
El error está en que los tres casos no son equiprobables, ya que para que haya un hombre y una mujer, puede ser que el primer hijo sea un hombre, y el segundo una mujer, o bien que la primera sea una mujer, y el segundo un hombre. Lo resolveremos correctamente en el próximo ejemplo.
Así pues, cuando queramos aplicar la regla de Laplace, normalmente consideraremos nuestro espacio muestral ordenado, como hemos hecho hasta ahora, para evitar errores.
Veamos cómo se aplica correctamente esta regla.
Ejemplo
Si en una familia hay dos hijos, y suponemos que la probabilidad de ser hombre es la misma que la de ser mujer, ¿cuál es la probabilidad de que los dos hijos sean del mismo sexo?
Como vamos a aplicar la regla de Laplace, consideraremos los resultados ordenados.
En este caso, nuestro espacio muestral es
![]()
Los casos favorables son y . Por lo tanto, la probabilidad es de
4.1. Probabilidad de un evento simple | Ejemplo 1
4.2. Probabilidad (I) Regla de Laplace
5. Diagrama del árbol
Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad.
En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final).
Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1
Ejemplo 1Una clase consta de seis niñas y 10 niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
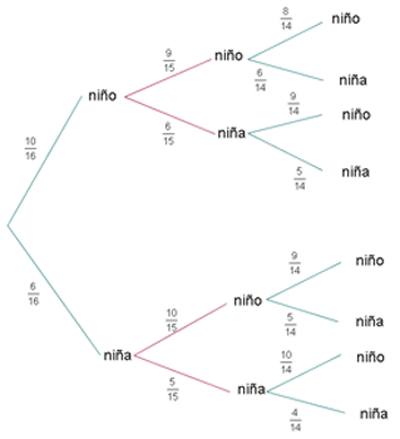
1. Seleccionar tres niños.
Son sucesos independientes
![]()
2. Seleccionar exactamente dos niños y una niña.
![]()
3. Seleccionar exactamente dos niñas y un niño.
![]()
4. Seleccionar tres niñas.
![]()
Ejemplo 2
Calcular la probabilidad de que al arrojar al aire tres monedas, salgan:
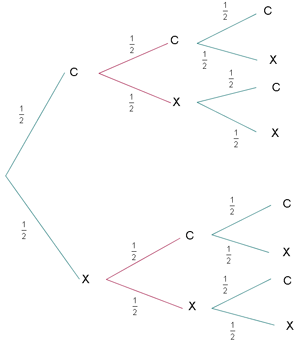
1. Tres caras.
![]()
5.1. Diagrama en árbol, probabilidad
5.2. Diagrama de arbol 1 de 3