LA FORMA Y EL NÚMERO EN SITUACIONES DE LA COTIDIANIDAD.

5.3. Procedimiento para la determinación del valor numérico de una variable en una ecuación de 1er grado.

El valor numérico de una expresión algebraica es el número que resulta de sustituir las variables de la de dicha expresión por valores concretos y completar las operaciones. Una misma expresión algebraica puede tener muchos valores numéricos diferentes, en función del número que se asigne a cada una de las variables de la misma.

La única precaución necesaria es respetar el orden y las propiedades de las operaciones. Por ejemplo, no tiene sentido calcular el valor numérico de  para , porque no se puede dividir entre cero. En la siguiente animación puedes ver cómo se haría la sustitución para calcular el valor numérico de  para ,  y . Faltaría completar las operaciones (el resultado final es ), pero lo más importante es que te fijes en los elementos que se añaden al hacer la sustitución: El punto del producto entre el 3 y el 2 (valor de ) y los paréntesis de -1 (valor de ), que son necesarios para indicar la multiplicación con el 2.

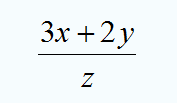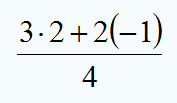
El punto de la multiplicación se puede omitir entre el 2 y el -1 gracias a los paréntesis, aunque escribirlo no sería un error. Fíjate en los siguientes ejemplos, en los que puedes ver cómo calcular el valor numérico de varias expresiones, paso a paso, para distintos valores de las variables.

EXPRESIÓN ALGEBRAICA	VALORES DE LAS VARIABLES	VALOR NUMÉRICO PARA ESOS VALORES DE LAS VARIABLES