LA FORMA, EL NÚMERO Y LA RELACIÓN CON EL ENTORNO NATURAL Y CULTURAL
5. Teorema de Pitágoras en las culturas ancestrales.
5.2. Demostración gráfica y analítica del Teorema de Pitágoras
El teorema de Pitágoras
En primer lugar deberíamos recordar un par de ideas:
- Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
- En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos
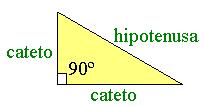
¿Qué es el teorema de Pitágoras?
Tenemos una página que explica el Teorema de Pitágoras, pero aquí tienes un breve resumen:
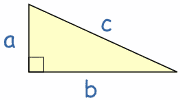
El teorema de Pitágoras dice que en un triángulo rectángulo, el cuadrado de a (a²) más el cuadrado de b (b²) es igual el cuadrado de c (c²):
a2 + b2 = c2
Demostración del teorema de Pitágoras usando álgebra
Podemos ver que a2 + b2 = c2 usando el Álgebra
Mira este diagrama... tiene dentro un triángulo "abc" (en realidad tiene cuatro):
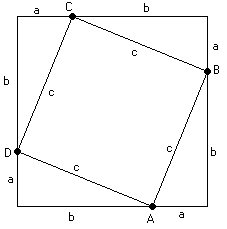
Es un gran cuadrado, cada lado mide a+b, así que el área es:
A = (a+b)(a+b)
Ahora sumamos las áreas de los trozos más pequeños:
Y hay cuatro triángulos, cada uno con área A =½ab
Así que los cuatro juntos son A = 4(½ab) = 2ab
Si sumamos el cuadrado inclinado y los 4 triángulos da: A = c²+2ab
El área del cuadrado grande es igual al área del cuadrado inclinado y los 4 triángulos. Esto lo escribimos así:
(a+b)(a+b) = c²+2ab
Ahora, vamos a operar a ver si nos sale el teorema de Pitágoras:
Empezamos con: (a+b)(a+b) = c²+2ab
Desarrollamos (a+b)(a+b): a²+2ab+b² = c²+2ab
Restamos "2ab" de los dos lados: a²+b² = c²
