SISTEMAS DE NUMERACIÓN, OPERACIONES CON NÚMEROS ENTEROS (Z) Y RACIONALES (Q).
4. Origen de los Enteros.
4.1. Operaciones en Z: Adición y sustracción, multiplicación y división, sus propiedades aplicadas a la vida cotidiana.
Suma de números enteros
1. Si los números enteros tienen el mismo signo, se suman los valores absolutos y al resultado se le coloca el signo común.
3 + 5 = 8
(−3) + (−5) = − 8
2. Si números enteros son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le coloca el signo del número de mayor valor absoluto.
− 3 + 5 = 2
3 + (−5) = − 2
Propiedades de la suma de números enteros1. Interna:
a + b ϵ ℜ
3 + (−5) = -2
2. Asociativa:
(a + b) + c = a + (b + c) ·
(2 + 3) + (− 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0 = 0
3. Conmutativa:
a + b = b + a
2 + (− 5) = (− 5) + 2
− 3 = − 3
4. Elemento neutro:
a + 0 = a
(−5) + 0 = − 5
5. Elemento opuesto
a + (-a) = 0
5 + (−5) = 0
−(−5) = 5
Resta de números enterosLa diferencia de los números enteros se obtiene sumando al minuendo el opuesto del sustraendo.
a - b = a + (-b)
7 − 5 = 2
7 − (−5) = 7 + 5 = 12
Propiedades de la resta de números enteros
1.Interna:
a − b ϵ ℜ
10 − (−5) =15
2. No es Conmutativa:
a - b ≠ b - a
5 − 2 ≠ 2 − 5
Multiplicación de números enterosLa multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
Regla de los signos
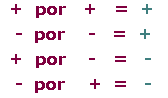
2 · 5 = 10
(−2) · (−5) = 10
2 · (−5) = − 10
(−2) · 5 = − 10
Propiedades de la multiplicación de números enteros
1. Interna:
a · b ϵ ℜ
2 · (−5) =-10
2. Asociativa:
(a · b) · c = a · (b · c)
(2 · 3) · (−5) = 2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
3. Conmutativa:
a · b = b · a
2 · (−5) = (−5) · 2
-10 = -10
4. Elemento neutro:
a ·1 = a
(−5)· 1 = (−5)
5. Distributiva:
a · (b + c) = a · b + a · c
(−2)· (3 + 5) = (−2) · 3 + (−2) · 5
(−2)· 8 =- 6 - 10
-16 = -16
6. Sacar factor común:
a · b + a · c = a · (b + c)
(−2) · 3 + (−2) · 5 = (−2) · (3 + 5)
División de números enterosLa división de dos números enteros es otro número entero, que tiene como valor absoluto el cociente de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Propiedades de la división de números enteros1. No es una operación interna:
(−2) : 6 No pertenece enteros
2. No es Conmutativo:
a : b ≠ b : a
6 : (−2) ≠ (−2) : 6