SISTEMAS DE NUMERACIÓN, OPERACIONES CON NÚMEROS ENTEROS (Z) Y RACIONALES (Q).
2. Sistema de numeración binario: Operaciones en el sistema binario (adición, sustracción, multiplicación y división)
Actualmente la mayoría de las personas utilizamos el sistema decimal (de 10 dígitos) para realizar operaciones matemáticas. Este sistema se basa en la combinación de 10 dígitos (del 0 al 9). Construimos números con 10 dígitos y por eso decimos que su base es 10. Por ejemplo el 23, el 234, 1093 etc. Todos son dígitos del 0 al 9.Pero hay otro sistema o lenguaje muy utilizado que es el sistema binario de numeración, que en algunos casos, como por ejemplo en informática, se puede llamar Lenguaje Binario, debido a que es el lenguaje que usamos para entendernos con el ordenador
El sistema binario es un sistema de numeración en el que los números se representan utilizando las cifras 0 y 1, es decir solo 2 dígitos (bi = dos). Esto en informática y en electrónica tiene mucha importancia ya que las computadoras trabajan internamente con 2 niveles: hay o no hay de Tensión, hay o no hay corriente, pulsado o sin pulsar, etc.
Esto provoca que su sistema de numeración natural sea el binario, por ejemplo 1 para encendido y 0 para apagado. También se utiliza en electrónica y en electricidad (encendido o apagado, activado o desactivado, etc.). El lenguaje binario es muy utilizado en el mundo de la tecnología.

Números Binarios
Como ya dijimos, el sistema binario se basa en la representación de cantidades utilizando los números 1 y 0. Por tanto su base es 2 (número de dígitos del sistema). Cada dígito o número en este sistema se denomina bit (contracción de binary digit).
Por ejemplo el número en binario 1001 es un número binario de 4 bits. Recuerda "cualquier número binario solo puede tener ceros y unos".
Los Números Binarios empezarían por el 0 (número binario más pequeño) después el 1 y ahora tendríamos que pasar al siguiente número, que ya sería de dos cifras porque no hay más números binarios de una sola cifra.
El siguiente número binario, por lo tanto, sería combinar el 1 con el 0, es decir el 10 (ya que el 0 con el 1, sería el 01 y no valdría porque sería igual que el 1), el siguiente sería el número el 11. Ahora ya hemos hecho todas las combinaciones posibles de números binarios de 2 cifras, ya no hay más, entonces pasamos a construir los de 3 cifras. El siguiente sería el 100, luego el 101, el 110 y el 111. Ahora de 4 cifras...
Según el orden ascendente de los números en decimal tendríamos los números binarios equivalentes a sus números en decimal :
El 0 en decimal sería el 0 en binario
El 1 en decimal sería el 1 en binario
El 2 en decimal sería el 10 en binario (recuerda solo combinaciones de 1 y 0)
El 3 en decimal sería el 11 en binario

Y así sucesivamente obtendríamos todos los números en orden ascendente de su valor, es decir obtendríamos el Sistema de Numeración Binario y su número equivalente en decimal.
Pero que pasaría si quisiera saber el número equivalente en binario al 23.456 en decimal. Tranquilo, hay un método para convertir un número decimal en binario sin hacerlo uno a uno.
Decimal a Binario
Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).
Para sacar la cifra en binario cogeremos el último cociente (siempre será 1) y todos los restos de las divisiones de abajo arriba, orden ascendente.
Ejemplo queremos convertir el número 28 a binario:
28 dividimos entre 2 : Resto 0
14 dividimos entre 2 : Resto 0
7 dividimos entre 2 : Resto 1
3 dividimos entre 2 : Resto 1 y cociente final 1
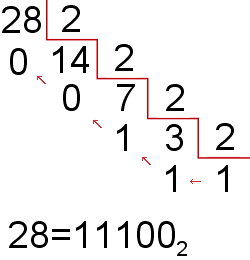
Entonces el primer número del número equivalente en binario sería el cociente último que es 1 y su resto que es también 1, la tercera cifra del equivalente sería el resto de la división anterior que es 1, el de la anterior que es 0 y el último número que cogeríamos sería el resto de la primera división que es 0.
Con todos estos número quedaría el número binario: 11100.
Conclusión el número 28 es equivalente en binario al 11.100.
Vemos como para sacar el equivalente se coge el último cociente de las operaciones y los restos que han salido en orden ascendente (de abajo arriba) 11100.
El subíndice 2 que hemos puesto al final del número en binario, es para indicar que es un número en base 2, pero no es necesario ponerlo.
Veamos otro ejemplo el número 65 pasarlo a binario.
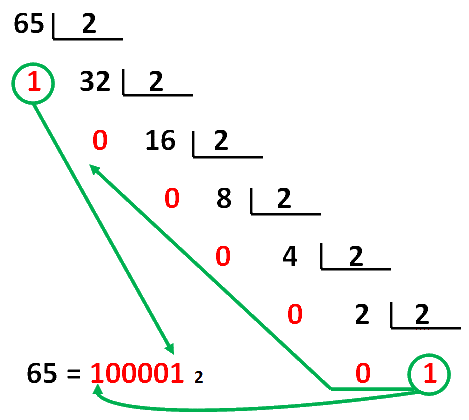
Pues ahora al revés. ¿Que pasaría si quisiera saber cual es el número equivalente en decimal del número binario por ejemplo 1001? Pues también hay método.
PASO 1 – Numeramos los bits de derecha a izquierda comenzando desde el 0 (muy importante desde 0 no desde 1).
PASO 2 – Ese número asignado a cada bit o cifra binaria será el exponente que le corresponde.
PASO 3 – Cada número se multiplica por 2 elevado al exponente que le corresponde asignado anteriormente.
PASO 4 - Se suman todos los productos y el resultado será el número equivalente en decimal
Vamos a verlo paso a paso con un ejemplo y gráficamente que será más sencillo de entender.
Ejemplo el número 1001 queremos saber su equivalente en decimal. Primero asignamos exponentes:
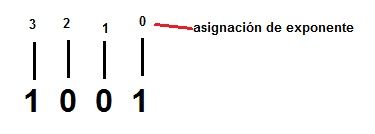
Empezamos por el primer producto, que será el del primer número binario por 2 elevado a su exponente, es decir 1 x 23 .
OJO Recuerda que cualquier número elevado a cero es 1, por ejemplo 2 elevado a 0 es = 1.
El segundo y el tercer productos serán 0 por que 0 x 22 y 0 x 21 su resultado es 0 y el último producto será 1 x 20 que será 1, luego 1 x 20 es 1 (no confundir y poner 0).
Ya estamos en el último paso que es sumar el resultado de todos estos productos:
1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8 + 0 + 0 + 1 = 9
El equivalente en decimal del número binario 1001 es el 9.
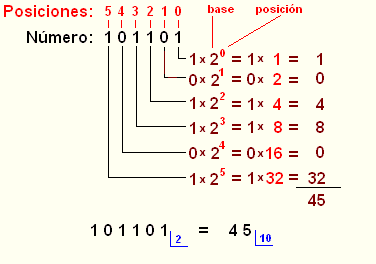
Veamos otro ejemplo solo gráficamente para que lo entiendas definitivamente. En este caso la asignación del exponente a cada número ya lo hacemos directamente en los productos, que es como se suele hacer normalmente.
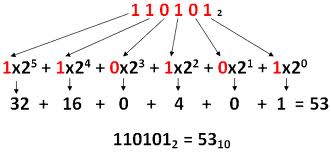
Otro ejemplo con todos los datos:
Operaciones Binarias
Las operaciones binarias que se pueden realizar con número binarios son las mismas que en cualquier otro sistema: suma, resta, multiplicación y división. Veamos algunos Ejemplos de Operaciones Binarias.
Suma de Números Binarios
Las posibles combinaciones al sumar dos bits son
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Un ejemplo con más cifras:
100110101
+ 11010101
———————
1000001010
A continuación se suman los números de la siguiente columna: 0 + 0 = 0, pero como nos tenemos que sumar el 1 de la anterior suma, el resultado será 0 + 1 = 1.
Así seguimos hasta terminar todas la columnas (exactamente como en decimal).
Resta de Números Binarios
Las restas básicas 0-0, 1-0 y 1-1 son evidentes:
0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = Es una resta imposible en binario porque no hay números negativos.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sumándola, a la posición siguiente. Veamos algunos ejemplos:
Dos ejemplos más:
10001 11011001
-01010 -10101011
—————— ————
00111 00101110
Multiplicación de Números Binarios
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Por ejemplo, multipliquemos 10110 por 1001:
10110
x 1001
——————
10110
00000
00000
10110
———————
11000110
División de Números Binarios
Igual que en el producto, la división es muy fácil de realizar, porque no son posibles en el cociente otras cifras que no sean UNOS y CEROS.
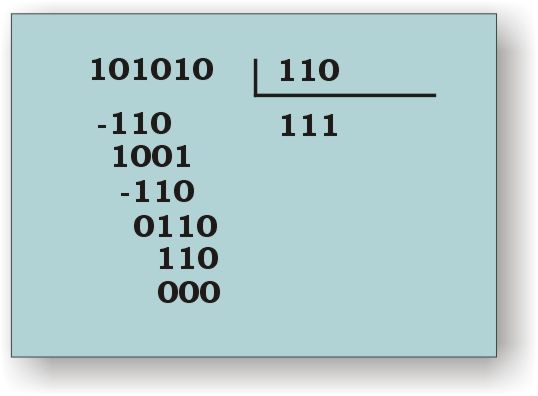
Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).
Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO. En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente.
El procedimiento de división continúa del mismo modo que en el sistema decimal.