APLICACIÓN DE LA ENERGÍA EN LOS PROCESOS PRODUCTIVOS
2. Trabajo y su relación con la energía cinética
Trabajo y energía cinética
Vamos a tratar en este artículo el concepto de trabajo y su relación con la energía cinética, mencionada ya en el artículo sobre energía mecánica.
La noción de energía es uno de los conceptos mas básicos en física y en efecto en todas las ciencias. La energía puede tomar muchas formas pero la forma particular que nos interesa en este artículo es la energía contenida en un cuerpo debido a su movimiento, la energía cinética. El trabajo (como concepto físico) hecho sobre un cuerpo implica que una fuerza actúe en él durante un desplazamiento. Veremos como la energía cinética de un cuerpo cambia cuando sobre él se realiza un trabajo lo que se conoce como teorema trabajo-energía, y como estos resultados nos pueden permitir entender diversos aspectos del movimiento y resolver problemas que pueden ser dificultosos de resolver utilizando la segunda ley de Newton directamente. Una vez que hayamos aprendido a calcular el trabajo, tendremos una poderosa herramienta para la comprensión del movimiento.
La energía cinética y las fuerzas constantes
La solución de las ecuaciones de movimiento partiendo de la segunda ley de Newton, F = ma, dan la posición del vector desplazamiento como función del tiempo, sin embargo tales soluciones pueden ser difíciles. Existe una vía para encontrar las soluciones a las ecuaciones de movimiento donde se puede esquivar el problema de cómo la posición del cuerpo varía con el tiempo. Con este nuevo enfoque podemos relacionar el desplazamiento de un cuerpo sometido a una fuerza con su rapidez*.
En el artículo sobre movimiento rectilíneo llegamos a las expresiones de cálculo del desplazamiento y la velocidad de un cuerpo que se mueve bajo la acción de una fuerza constante, las que pueden exponerse como:
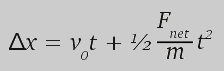 (ecuación 1)
(ecuación 1)
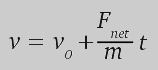 (ecuación 2)
(ecuación 2)
El desplazamiento Δx es x - x0 , donde la posición x varía con el tiempo y x0 es la posición al tiempo t = 0. Para eliminar el tiempo, lo despejamos en la ecuación 2 y los sustituimos en la ecuación 1. Cancelando los términos iguales y reorganizando podemos llegar a que:
Fnet
Δx = ½mv2 - ½mv02 (ecuación 3)
Esta expresión es todo lo que necesitamos para saber cuan rápido se mueve un cuerpo en el que actúa una fuerza neta constante después de haber viajado una distancia.
La cantidad de la izquierda de la ecuación 3 es el trabajo neto, wnet, hecho por la fuerza neta sobre el cuerpo, de forma que para una fuerza constante en una dimensión:
wnet = Fnet Δx (ecuación 4)
De esta forma podemos definir con palabras el concepto de trabajo:
Como el producto de la magnitud de la fuerza neta aplicada a un cuerpo por el desplazamiento que realiza el cuerpo.
Por su parte el término de la derecha de la ecuación 3 representa el cambio de la energía cinética contenida en el cuerpo debido al trabajo aplicado, ya que como sabemos del artículo energía mecánica:
Ec = ½mv2 (ecuación
5)
La energía cinética es un escalar no negativo y depende solamente de la magnitud de la velocidad, es decir de la rapidez.
El trabajo es un concepto tan importante que se ha reservado un nombre especial para su unidad, el joule en honor a James Joule que desarrolló importantes trabajos en este campo.
Un joule (J), es el trabajo realizado por una fuerza de 1N cuando ha movido un cuerpo una distancia de 1m. La ecuación 3 nos indica que dada la igualdad, la energía cinética (al igual que cualquier otra forma de la energía) también se pueden medir en joules. Si se fija, por definición el trabajo nos queda en N·m, mientras la energía cinética está en kg·m2/s2. No es difícil demostrar que 1N·m = 1kg·m2/s2.
En el lenguaje coloquial la palabra trabajo tiene diferentes significados, no se puede confundir la connotación coloquial con la definición precisa dada por la ecuación 4. Muchas veces en la vida diaria la palabra trabajo se usa en concordancia con la definición científica, estamos de acuerdo que para arrastrar una caja por el piso tenemos que hacer un trabajo. En este caso hay plena concordancia, se hace una fuerza y se produce un desplazamiento. Pero también acostumbramos a llamar trabajo al que hacemos cuando sostenemos estacionario un objeto en los brazos tal como una bolsa de mercado, aquí no hay trabajo ya que no hay desplazamiento.
El teorema trabajo-energía
Miremos de nuevo a la ecuación 3. Suponga que un cuerpo se mueve bajo la influencia de una fuerza neta constante, desde una posición inicial xi a una posición final xf , es decir, tiene un desplazamiento Δx = xf - xi . Como cambia su rapidez lo hace también su energía cinética. El cambio de la energía cinética, ΔEc, está dado por:
ΔEc
= Ecf - Eci
(ecuación 6)
Observe que el término de la derecha de la ecuación 6 corresponde plenamente con el de la ecuación 3, por lo que:
Wnet = ΔEc
(ecuación 7)
La ecuación 7 se conoce como el teorema trabajo-energía, que se podía enunciar como:
"Cuando sobre un cuerpo se realiza trabajo, se produce un cambio de igual magnitud en su energía cinética."
Como sabemos, el trabajo es el producto de dos magnitudes
vectoriales, fuerza y desplazamiento, de esto se desprende que el trabajo
también será vectorial, pero como estamos trabajando en un sistema
uni-direccional, tanto la fuerza neta como el desplazamiento quedan
completamente definidos asignándoles un signo, de esta forma, el trabajo se
considera positivo cuando la fuerza neta está en la misma dirección que el
desplazamiento y de signo negativo cuando la fuerza neta está en la dirección
contraria al desplazamiento. Lo que significa, en términos de la energía
cinética, que cuando el trabajo es positivo, aumenta la energía cinética del
cuerpo y cuando es negativo la reduce.
Supongamos que lanzamos una piedra hacia arriba. Mientras la piedra sube, el
signo del desplazamiento es contrario a la fuerza de la gravedad
que está actuando en ella (el desplazamiento es hacia arriba y la gravedad es
hacia abajo), se está realizando trabajo negativo sobre la piedra, y de acuerdo
al teorema trabajo-energía, la energía cinética de la piedra está bajando. Una
vez que alcanza la altura máxima la piedra se detiene, ha perdido toda su
energía cinética (v = 0), comienza entonces el descenso, ahora el
trabajo es positivo (la gravedad y el desplazamiento son en la misma dirección)
y la energía cinética vuelve a subir gradualmente hasta llegar a ser del valor
inicial, cuando la piedra llegue al punto de partida (estamos considerando que
no hay pérdidas de energía por rozamiento con el aire).
Pero, sorpresivamente al llegar al punto de partida el trabajo neto es cero, no
se ha hecho trabajo neto sobre la piedra, ya que el desplazamiento final es
también cero. No es difícil darse cuenta que los signos positivo y negativo de
trabajos iguales de ida y de vuelta hacen que se anulen mutuamente.
El teorema trabajo-energía es útil en realidad si podemos calcular el trabajo. En la mayoría de los casos reales sobre el cuerpo actúan más de una fuerza, por ejemplo, si bajamos un cubo al fondo de un pozo a través de una cuerda que gira en una polea, para coger con él agua, sobre el cubo actúan dos fuerzas, la tensión en la cuerda y la fuerza de la gravedad. Si el descenso del cubo es lento y a velocidad constante es por qué estamos haciendo en la cuerda una fuerza que anula la gravedad, en este caso la fuerza neta es cero y por tanto el trabajo es también cero. No obstante, podemos decir que la cuerda está haciendo trabajo negativo sobre el cubo en la misma magnitud, pero de dirección contraria al que hace la gravedad que es positivo, y, de hecho, el trabajo neto en cualquier punto del recorrido es cero porque sus signos se anulan mutuamente.
Trabajo en sistemas de dos y tres dimensiones.
Ya sabemos que la energía cinética tiene una dependencia cuadrática de la velocidad del cuerpo portador de la energía, y como el cuerpo puede moverse en una sola dirección, la energía cinética tiene una referencia uni-direccional, esto significa que es dependiente solamente de la magnitud de la velocidad, es decir de la rapidez. Ahora trataremos de extender los conceptos de energía cinética, trabajo y el teorema trabajo-energía a dos y tres dimensiones. Continuemos asumiendo que la fuerza neta es constante, pero ahora debe utilizarse su naturaleza plena de vector, al igual que con el desplazamiento, la velocidad y la aceleración (dejaremos de utilizar el sub-índice "net" de la fuerza para reducir la complejidad de la escritura de las expresiones).
La aplicación de la energía y el trabajo en dos y tres dimensiones se simplifica, porque las fuerzas y sus efectos sobre el movimiento se pueden aplicar de forma independiente en las diferentes direcciones cartesianas.
Usemos un sistema bi-direccional por simplicidad. En este caso la ecuación 3, que relaciona el trabajo y la energía se puede descomponer en dos expresiones de acuerdo a la dirección de los ejes cartesianos como:
Fx Δx = ½mvx2 - ½mvx02 (ecuación 8)
Fy Δy = ½mvy2 - ½mvy02 (ecuación 9)
Donde tanto la fuerza, como la velocidad y el desplazamiento han sido separados en sus componentes. Ya sabemos que la energía cinética, depende de la magnitud de la velocidad, es decir de la rapidez, si sumamos los dos componentes cuadráticos x e y de la magnitud de la velocidad de las ecuaciones 8 y 9 llegamos a que la rapidez es:
v2 = vx2 + vy2 (ecuación 10)
La suma ejecutada nos hace llegar a la expresión generalizada del teorema trabajo-energía:
Fx Δx + Fy Δy = ½mv2 - ½mv02 (ecuación 11)
Extendiendo el razonamiento a tres dimensiones llegamos a que para una fuerza F constante:
w = Fx Δx + Fy Δy + Fz Δz (ecuación 12)
Video de Teorema de trabajo y energia cinetica